Лабораторная работа № 2.

Тема: Элементы комбинаторики. Дополнительные методы и приемы.

Цель: изучение средств пакета MS Excel для реализации возможности вычислений по основным формулам комбинаторики (сочетания, размещения, перестановки).

Теоретические сведения:

1. Полиномиальные коэффициенты.

Пусть дано множество . Построим из него кортеж состава 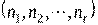в котором элемент встречается 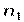, элемент - 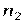раз и т.д. элемент 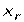используется раз. Порядок элементов в составном кортеже существенен, но перестановка местами разных копий одного и того же элемента 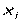на кортеж не влияет, т.е. копии одного и того же элемента считаются неотличимыми. Общее количество использованных элементов равно . Такие кортежи называются перестановками с повторениями. Их количество вычисляется по формуле .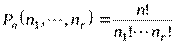

Пример. Сколькими способами можно расставить белые фигуры: 2 ладьи, 2 слона, 2 коня, ферзь и король на первой линии шахматной доски?

Решение. Рассматриваемые кортежи имеют длину 8 и состоят из элементов пяти видов. Состав кортежей имеет вид (2, 2, 2, 1, 1). Следовательно, число способов, которыми можно расставить 8 фигур на первой линии шахматной доски, равно

.

Данную задачу удобно понять в рамках стандартной урновой схемы: Имеется 8 различных шаров (позиций горизонтали) и 5 урн(классов фигур). Сколько способов распределить 8 различных шаров по 5 урнам так, что в первую урну(ладьи) попадает 2 шара, вторую(слоны) – также 2 и т.д. формируя распределение шаров по урнам вида (2,2,2,1,1). Наиболее точно данная комбинаторная задача специфицируется путем использования понятия функции. Искомое число это количество отображений следующего вида:

Пример. Число различных слов, которое получим, переставляя буквы слова «математика», равно , так как мы распределяем 10 различных позиций слова между классами букв :‘м’, ’а, ’т’ и т.д.

2. Сочетания с повторениями.

Если порядок различных элементов в составном кортеже не важен, а имеет место только состав кортежа , то получаем неупорядоченные кортежи с повторениями или сочетания с повторениями. Таких сочетаний имеется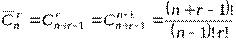

Пример. В цветочном магазине продаются цветы шести сортов. Сколько можно составить различных букетов из десяти цветов в каждом? (Букеты, отличающиеся лишь расположением цветов, считаются одинаковыми.)

Решение. Рассматриваемое множество состоит из шести различных элементов, а кортежи имеют длину 10. Поскольку порядок расположения цветов в букете не играет роли, то число букетов равно числу сочетаний с повторениями из шести элементов по десяти в каждом. Следовательно, можно составить = 3003 различных букетов.

Пример. Сколько решений имеет уравнение

где каждое — неотрицательное целое число?

Решение. Решить уравнение равносильно задаче сформировать букет из 25 цветков используя цветки 5 типов 1-5 в некоторых неотрицательных количествах 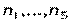. Поэтому иско-мое количество решений данного уравнения - это количество раз-личных сочетаний из 5 элементов по 25 с повторениями. Итак, существуют

различных решений уравнения .