Общая теория выборок и размещения шаров в урнах.

Пусть и - множество, упорядоченное своими индексами , т.е. считаем, что 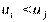, если . Выборкой объема из множества называется отображение , т.е. - некоторый набор из элементов из множества . Выборки различаются по критерию упорядоченности и наличия повторений. Множество всех отображений обозначается через или 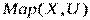и называется множеством упорядоченных выборок с повторениями. Отображение называется инъективным, если при выполняется неравенство .

Множество всех инъективных отображений обозначается как и называется множеством выборок без повторений. Выборка с повторениями получается в результате случайного эксперимента, когда выбираемый элемент снова возвращается в генеральную совокупность и может повторно встречаться в выборке сколь угодно раз. Выборка с повторениями называется также выборкой с возращением. В выборке без повторений, т.е. если эта выборка является элементом множества каждый элемент может встречаться только один раз и такая выборка формируется в результате случайного эксперимента без возвращения выбранных объектов. Отображение называетсямонотонным, если из условия следует неравенство . Множество монотонных отображений обозначается . Множество монотонных отображений называется множеством неупорядоченных выборок (с повторениями), т.к. монотонность выборки означает что мы расположили объекты, полученные в случайном эксперименте в стандартном порядке возрастания, т.е. их порядок не важен и объекты могут быть взаимно переставлены, так, что получится монотонная последовательность. Отображение называется строгомонотонным, если из условия следует неравенство . Множество строго монотонных отображений обозначается . Ясно, что имеет место формула . Множество 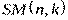называется также множеством неупорядоченных выборок без повторений.

Введем следующие обозначения :

- число упорядоченных выборок без повторений или число размещений из по без повторений;

- число упорядоченных выборок с повторениями или число размещений из по 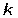с повторениями;

- число неупорядоченных выборок без повторений или число сочетаний из по без повторений;

- число неупорядоченных выборок с повторениями или число сочетаний из по с повторениями;

Теорема. Имеют место равенства:

;

;

;

.

Различные типы выборок имеют наглядную интерпретацию как схемы размещения шаров по урнам. Упорядоченным выборкам соответствует случай, когда все шары различимы (например, пронумерованы), а неупорядоченные выборки случай, когда все шары одинаковы. Выборкам с повторениями соответствуют размещения без запрета, когда в любой ячейке может быть любое количество шаров. В случае выборок без повторений используются размещения с запретом, когда в каждом ящике может находиться не более одного шара.

При этом все размещения с повторениями двух различных шаров выглядят так:

А размещения с повторениями одинаковых шаров следующим образом:

Для соответствующих размещений с запретом имеем следующие диаграммы: