Т - критерий Вилкоксона

Назначение критерия

Критерий применяется для сопоставления показателей,, измеренных в двух разных условиях на одной и той же выборке испытуемых. Он позволяет установить не только направленность изменений, но и их выраженность. С его помощью мы определяем, является ли сдвиг показателей в каком-то одном направлении более интенсивным, чем в другом.

Описание критерия Т

Этот критерий применим в тех случаях, когда признаки измерены по крайней мере по шкале порядка; и сдвиги между вторым и первым замерами тоже могут быть упорядочены. Для этого они должны варьировать в достаточно широком диапазоне. В принципе, можно применять критерий Т и в тех случаях, когда сдвиги принимают только три значения: —1, 0 и +1, но тогда критерий Т вряд ли добавит что-нибудь новое к тем выводам, которые можно было бы получить с помощью критерия знаков. Вот если сдвиги изменяются, скажем, от —30 до +45, тогда имеет смысл их ранжировать и потом суммировать ранги.

Подсчет критерия Т Вилкоксона

1. Составить список испытуемых в любом порядке, например, алфавитном.

2. Вычислить разность между индивидуальными значениями во втором и первом замерах ("после" - "до"). Определить, что будет считаться "типичным" сдвигом и сформулировать соответствующие гипотезы.

3. Перевести разности в абсолютные величины и записать их отдельным столбцом (иначе трудно отвлечься от знака разности).

4. Проранжировать абсолютные величины разностей, начисляя меньшему значению меньший ранг. Проверить совпадение полученной суммы рангов с расчетной.

5. Отметить кружками или другими знаками ранги, соответствующие сдвигам в "нетипичном" направлении.

6. Подсчитать сумму этих рангов по формуле: где Rr - ранговые значения сдвигов с более редким знаком.

7. Определить критические значения Т для данного п по Табл. VI Приложения 1. Если Тэмп меньше или равен Ткр, сдвиг в "типичную" сторону по интенсивности достоверно преобладает.

Критерий Фридмана

Назначение критерия

Критерий применяется для сопоставления показателей, измеренных в трех или более условиях на одной и той же выборке испытуемых. Критерий позволяет установить, что величины показателей от условия к условию изменяются, но при этом не указывает на направление изменений. Описание критерия Данный критерий является распространением критерия Т Вилкоксона на большее, чем 2, количество условий измерения. Однако здесь мы ранжируем не абсолютные величины сдвигов, а сами индивидуальные значения, полученные данным испытуемым в 1, 2, 3 и т. д. замерах.

Подсчет критерия ·2r Фридмана

1. Проранжировать индивидуальные значения первого испытуемого, полученные им в 1-м, 2-м, 3-м и т. д. замерах.

2. Проделать то же самое по отношению ко всем другим испытуемым.

3. Просуммировать ранги по условиям, в которых осуществлялись замеры. Проверить совпадение общей суммы рангов с расчетной суммой.

4. Определить эмпирическое значение ·2 r по формуле:

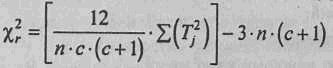
где с - количество условии; п - количество испытуемых; Ti - суммы рангов по каждому из условий.

5. Определить уровни статистической значимости для ·2 r

6. При большем количестве условий и/или испытуемых - определить количество степеней свободы v по формуле: v=c-1, где с - количество условий (замеров).

Определить критические значения критерия ·2 при данном числе степеней свободы V. Если ·2 r эмп равен критическому значению ·2 или превышает его, различия достоверны.

3.5. L - критерий тенденций Пейджа

Назначение L - критерия тенденций

Критерий L Пейджа применяется для сопоставления показателей, измеренных в трех и более условиях на одной и той же выборке испытуемых.

Критерий позволяет выявить тенденции в изменении величин признака при переходе от условия к условию. Его можно рассматривать как продолжение теста Фридмана, поскольку он не только констатирует различия, но и указывает на направление изменений.

Описание критерия тенденций L

Критерий позволяет проверить наши предположения об определенной возрастной или ситуативно обусловленной динамике тех или иных признаков. Он позволяет объединить несколько произведенных замеров единой гипотезой о тенденции изменения значений признака при переходе от замера к замеру. Если бы не его ограничения, критерий был бы незаменим в "продольных", или лонгитюдинальных, исследованиях. К сожалению, имеющиеся таблицы критических значений рассчитаны только нанебольшую выборку (n<12) и ограниченное количество сопоставляемых замеров (с<6).