 |
Главная |
Математическое и статистическое обоснование выпускной квалификационной работы
|
из
5.00
|
Для получения количественной оценки результатов социологического исследования особое значение имеет применение математико-статистического метода расчета. Важное место в этом направлении занимают такие показатели как: средняя арифметическая взвешенная; средняя структурная, в частности, мода и медиана; показатели вариаций (среднеквадратичное отклонение и коэффициент вариаций).
Нами было проведено исследование мнения молодежи о проблеме наркомании и мерах по профилактике наркотизации в Нижнекамском муниципальном районе.
Проведем математические и статистические расчеты средних величин.
Наибольший интерес в анкете представляет вопрос: "Насколько осознана молодежью проблема наркотизации?". Ответы респондентов распределились следующим образом:
в высшей степени злободневной - 50,9 %;
достаточно злободневной - 39,1 %;
не очень злободневной - 4,3 %;
совершенно не злободневной - 2,7 %;
затрудняюсь ответить - 3 %.
Проставим баллы к этим ответам:
в высшей степени злободневной - 5 баллов;
достаточно злободневной - 4 балла;
не очень злободневной - 3 балла;
совершенно не злободневной - 2 балла;
затрудняюсь ответить - 1 бал.
В качестве средней величины используем моду (Мо).
Мода (Мо) показывает наиболее часто встречающиеся баллы. В данном случае мода это 5 балла (50,9 %). Иными словами, самый распространенный ответ "проблема наркотизации в высшей степени злободневная".
На порядковом уровне измерения основной средней величиной является медиана. Медиана (Ме) представляет собой середину ранжированного числового ряда. В данном случае медианой является 4 балла.
Внесем баллы к ответам ( 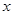 ), число респондентов (
), число респондентов ( 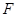 ) и дальнейшие расчеты в таблицу 11.
) и дальнейшие расчеты в таблицу 11.
Таблица 11 - Расчет средних величин и отклонений
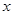
| 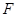 , в процентах , в процентах
| 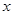 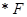
| 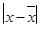
| 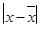 * F * F
| 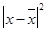
| 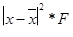
|
| 1 | 4 | 4 | 2,89 | 11,56 | 8,3521 | 33,4084 |
| 2 | 2 | 4 | 1,89 | 3,78 | 3,5721 | 7,1442 |
| 3 | 9 | 27 | 0,89 | 8,01 | 0,7921 | 7,1289 |
| 4 | 71 | 284 | 0,11 | 7,84 | 0,0121 | 0,8591 |
| 5 | 14 | 70 | 1,11 | 15,54 | 1,2321 | 17,2494 |
| ∑ | 100 | 389 | - | 46,73 | 13,9605 | 65,79 |
Определение средней арифметической взвешенной: [68, с.35-39]
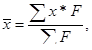 (1)
(1)
где 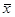 - средняя арифметическая взвешенная;
- средняя арифметическая взвешенная;
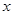 - оценка варианта ответа;
- оценка варианта ответа;
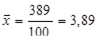
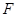 - число респондентов.
- число респондентов.
Расчет показывает, что средняя оценка, которую дали опрашиваемые сотрудники на данный вопрос составляет 3,89 балла.
Определение среднего линейного отклонения:
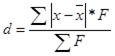 , (2)
, (2)
d = 46,73/100 = 0,4673
Определение среднего квадратического отклонения:
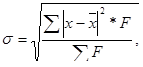 (3)
(3)
где 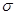 - среднее квадратичное отклонение;
- среднее квадратичное отклонение;
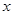 - оценка варианта ответа;
- оценка варианта ответа;
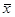 - средняя арифметическая взвешенная;
- средняя арифметическая взвешенная;
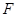 - число респондентов.
- число респондентов.
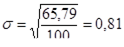
Расчет показывает, что среднее квадратическое отклонение составляет 0,81 балл, что говорит о средней степени согласованности среди опрошенной молодежи
Найдем коэффициент вариаций, как отношение среднего квадратичного отклонения к средней арифметической по формуле (4).
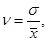 (4)
(4)
где 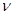 - коэффициент вариаций;
- коэффициент вариаций;
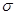 - среднее квадратичное отклонение;
- среднее квадратичное отклонение;
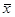 - средняя арифметическая взвешенная.
- средняя арифметическая взвешенная.
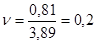
Чем ближе значение коэффициента вариации к нулю, тем больше степень согласованности среди респондентов. Полученный при расчетах коэффициент вариаций (0,2) показывает высокий уровень согласованности среди респондентов.
|
из
5.00
|
Обсуждение в статье: Математическое и статистическое обоснование выпускной квалификационной работы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

