 |
Главная |
Замкнутые отображения. Связь связности и послойной связности
|
из
5.00
|
Определение 15. Отображение f : X → Y называется замкнутым, если для каждого замкнутого множества F Í Х образ f (F) является замкнутым множеством в Y.
Определение 16. Отображение f : X → Y называется замкнутым над точкой yÎY, если для всякой окрестности О слоя f –1(y) Ì Х найдётся окрестность Oy точки y, трубка над которой f –1(Oy) содержится в данной окрестности О слоя f –1(y):
f –1(y) Í f –1(Oy) Í О.
Связь между замкнутостью в точке и общей замкнутостью устанавливает следующая
Лемма 2.1. Непрерывное отображение f : X → Y замкнуто тогда и только тогда, когда оно замкнуто над каждой точкой yÎY .
Доказательство. Необходимость. Пусть отображение f : X → Y замкнуто. Возьмём произвольную точку y Î Y и рассмотрим окрестность О множества f –1(y). Множество F = X \ О замкнуто в Х и F ∩ f –1(y) = Æ. Поэтому множество f (F) замкнуто в Y и точка y Ï f(F). Значит окрестность Oy = Y \ f (F) точки y обладает таким свойством f –1(Oy) ∩ F = Æ, следовательно, f –1(Oy) Ì О. Таким образом, отображение f замкнуто над каждой точкой yÎY в силу того, что точка y взята произвольно.
Достаточность. Пусть непрерывное отображение f замкнуто над каждой точкой yÎY. Предположим, что образ f (F) некоторого замкнутого в Х множества F не замкнут в Y . Пусть точка y Î [f ( F )] \ f(F), т.е. принадлежит границе множества f (F). Множество X \ F является окрестностью множества f –1(y). Следовательно, существует такая окресность Oy точки y, что f –1(Oy) Ì X \ F . Но тогда Oy ∩ f (F) = Æ и поэтому точка y Ï [f (F)].
Получили противоречие. Отсюда, отображение f замкнуто. €
Следующие утверждения указывают на некоторые важнейшие примеры замкнутых отображений.
Предложение 2.1. Непрерывное отображение f : X ® Y компактного пространства X в хаусдорфово пространство Y является замкнутым.
Доказательство. Рассмотрим произвольное множество F, замкнутое в Х. Оно будет компактным (по теореме 1.7). Тогда непрерывный образ f (F) компактного множества F будет компактен в Y (по теореме 1.9). Пространство Y хаусдорфово, следовательно, множество f (F) – замкнуто (в силу теоремы 1.8). Таким образом, отображение f является замкнутым.
Следствие 2.1. Биективное непрерывное отображение f : X ® Y компактного пространства X на хаусдорфово пространство Y является гомеоморфизмом.
Доказательство. Рассмотрим произвольное замкнутое подмножество F компактного пространства X. В силу предложения 2.1, образ f (F) – замкнутое множество. Тогда, по теореме 1.1, отображение f –1 является непрерывным, следовательно, f – гомеоморфизм.ÿ
Предложение 2.2. Пусть отображение f : X ® Y замкнуто над точкой y Î Y и пусть множество Z замкнуто в X. Тогда подотображение g = f | Z : Z ® Y замкнуто над точкой y. В частности, если отображение f замкнуто (над каждой точкой y Î Y), то и отображение g замкнуто.
Доказательство. Возьмём произвольную точку y Î Y и рассмотрим окрестность U Ì Z слоя g–1(y). Тогда в Х найдётся открытое множество U ¢ такое, что U = U ¢  Z. Множество O = U ¢
Z. Множество O = U ¢  (X \ Z) будет окрестностью слоя f –1(y) . Отображение f замкнутое над точкой y Î Y, поэтому найдётся такая окрестность Oy точки y, что f –1(Oy) Ì O. Тогда g–1(Oy) Ì Z
(X \ Z) будет окрестностью слоя f –1(y) . Отображение f замкнутое над точкой y Î Y, поэтому найдётся такая окрестность Oy точки y, что f –1(Oy) Ì O. Тогда g–1(Oy) Ì Z  O = Z
O = Z  U ¢ = U.
U ¢ = U.
В силу произвольности выбора точки y Î Y, можно заключить, что если отображение f замкнутое над каждой точкой y Î Y, то и отображение g замкнутое над каждой точкой y Î Y.
Предложение 2.3. Пусть отображение f : X ® Y замкнуто над точкой y Î T Í Y , где T – произвольное множество в Y .Тогдапод-отображение g = f |  : f –1(T) ® T замкнуто над точкой y . В частности, если отображение f замкнуто (над каждой точкой y Î T ), то и отображение g тоже замкнуто (над каждой точкой y Î T ).
: f –1(T) ® T замкнуто над точкой y . В частности, если отображение f замкнуто (над каждой точкой y Î T ), то и отображение g тоже замкнуто (над каждой точкой y Î T ).
Доказательство. Возьмём произвольную точку y Î T Í Y и некоторую окрестность О слоя g–1(y) = f –1(y), такую что
O = O '  f –1(T),
f –1(T),
где О ¢ – открытое в Х множество.Так как отображение f замкнутое над точкой y, найдётся такая окрестность O ' y в Y точки y, что f –1(O ' y) Ì О'. Тогда в Т существует такая окрестность Oy точки y, что Oy = Oy '  T, и f –1(Oy) = g–1(Oy) Ì O '
T, и f –1(Oy) = g–1(Oy) Ì O '  f –1(T) = О. Следовательно, отображение g будет замкнуто над y Î Y.
f –1(T) = О. Следовательно, отображение g будет замкнуто над y Î Y.
Если отображение f замкнутое над каждой точкой y, то и отображение g будет замкнутым над каждой точкой y.
Установим теперь связь между связными и послойно связными замкнутыми отображениями.
Предложение 2.4. Пусть отображение f : X→ Y замкнуто над точкой y Î Y и слой f –1(y) является несвязным множеством. Тогда отображение f несвязное над точкой y. В частности, если отображение f замкнуто и каждый его слой несвязен, то оно несвязное над каждой точкой y Î Y .
Доказательство. Поскольку слой f –1(y) является несвязным множеством, то найдутся такие непустые открытые в f –1(y) множества О1 и О2, что О1 ∩ О2 = Æ и О1  О2 = f –1(y). Тогда в Х существуют открытые множества Q1 и Q2 такие, что
О2 = f –1(y). Тогда в Х существуют открытые множества Q1 и Q2 такие, что
O1 = Q1  f –1(y), O2 = Q2
f –1(y), O2 = Q2  f –1(y).
f –1(y).
Рассмотрим замыкание этих множеств  и
и  в Х. Их пересечение
в Х. Их пересечение  есть замкнутое множество, и F
есть замкнутое множество, и F  f –1(y) = Æ (т.к. О1 и О2 замкнутые в f –1(y), как дополнения до открытых). Множество О = (Q1
f –1(y) = Æ (т.к. О1 и О2 замкнутые в f –1(y), как дополнения до открытых). Множество О = (Q1  Q2) \ F открыто в Х, причём f –1(y) Ì О. Для этой окрестности О (в силу замкнутости отображения f ) найдётся такая окрестность Oy точки y, что f –1(Oy) Ì О. Пусть G1 = f –1(Oy)
Q2) \ F открыто в Х, причём f –1(y) Ì О. Для этой окрестности О (в силу замкнутости отображения f ) найдётся такая окрестность Oy точки y, что f –1(Oy) Ì О. Пусть G1 = f –1(Oy) 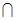 Q1 и G2 = f –1(Oy)
Q1 и G2 = f –1(Oy) 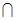 Q2 – открытые в f –1(Oy) множества. Так как
Q2 – открытые в f –1(Oy) множества. Так как
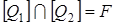 Ì Х \ f –1(Oy),
Ì Х \ f –1(Oy),
то G1 ∩ G2 = Æ. Тогда f –1(Oy) = G1  G2. Следовательно, трубка f –1(Oy) несвязна.
G2. Следовательно, трубка f –1(Oy) несвязна.
Пусть U Í Oy – произвольная окрестность точки y. Тогда 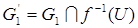 и
и  – дизъюнктные множества, открытые в f –1(U), и непустые, т.к. О1 Ì
– дизъюнктные множества, открытые в f –1(U), и непустые, т.к. О1 Ì  и О2 Ì
и О2 Ì 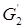 . Следовательно, для любой окрестности U Í Oy трубка f –1(U) несвязна. Отображение f несвязно над точкой y по определению.
. Следовательно, для любой окрестности U Í Oy трубка f –1(U) несвязна. Отображение f несвязно над точкой y по определению.
Если отображение f замкнутое над каждой точкой y Î Y и каждый его слой несвязн, тогда, для произвольной точки y, отображение f будет несвязным над ней, следовательно, и над каждой точкой y Î Y.
Из установленного предложения автоматически вытекает
Следствие 2.2. Пусть отображение f : X→ Y замкнуто над точкой y Î Y и связно над точкой y. Тогда слой f –1(y) является связным множеством. В частности, если f замкнутое и связное отображение, то оно послойно связное.
Предложение 2.5. Пусть отображение f : X→ Y замкнутое и послойно связное. Тогда оно связное.
Доказательство. Возьмём произвольную точку y Î Y и предположим, что отображение f несвязно над точкой y. Тогда существует такая окрестность Oy точки y, что трубка f –1(U) является несвязной над каждой окрестностью U Í Oy точки y. Зафиксируем некоторую такую связную окрестность U, для которой выполняются следующие условия:
f –1(U) = О1  О2, О1 ∩ О2 = Æ,
О2, О1 ∩ О2 = Æ,
где О1 и О2 – непустые открытые в f –1(U) множества.
Слой f –1(y) связен и f –1(y) Ì f –1(U), отсюда, f –1(y) содержится либо в О1, либо в О2 (по теореме 1.4). Рассмотрим произвольную точку х1ÎО1. Образ этой точки f (x1) = y1 Ì U. По условию, слой f –1(y1) связен и f –1(y1) Ì О1  О2 = f –1(U). Поскольку О1 ∩ О2 = Æ и х1ÎО1, следовательно (по теореме 1.4), f –1(y1) Ì О1. (Другими словами, если одна точка слоя принадлежит множеству О1, то и весь слой принадлежит этому множеству.)
О2 = f –1(U). Поскольку О1 ∩ О2 = Æ и х1ÎО1, следовательно (по теореме 1.4), f –1(y1) Ì О1. (Другими словами, если одна точка слоя принадлежит множеству О1, то и весь слой принадлежит этому множеству.)
Отсюда, так как точка х1 произвольная, то О1 = f –1( f (O1)). Аналогично доказывается, что О2 = f –1(f (O2)).
Отображение f замкнутое, тогда, по теореме 2.3, подотображение g = f : f –1(Oy) ® Oy также замкнутое. Таким образом, множества f (O1) = g (O1) и f (O2) = g (O2) будут непересекающимися открыто-замкнутыми в U и U = f (O1)  f (O2), т.е. окрестность U несвязна. Это противоречит выбору окрестности U.
f (O2), т.е. окрестность U несвязна. Это противоречит выбору окрестности U.
Для замкнутых отображений итоговую взаимосвязь между послойной связностью и связностью теперь можно выразить в форме следующей теоремы:
Теорема 2.3. Замкнутое отображение f : X→ Y связно тогда и только тогда, когда оно послойно связно.
(Вытекает из следствия 2.1 и предложения 2.5).
Из последней теоремы и предложений 2.2 – 2.3 получаются такие следствия:
Следствие 2.3. Пусть отображение f : X→ Y замкнутое, Z Í X замкнуто в Х. Подотображение g = f | Z : Z ® Y является связным тогда и только тогда, когда оно послойно связное.
Следствие 2.4. Пусть отображение f : X→ Y замкнутое, T Í Y произвольное множество. Подотображение g = f |  : f –1(T) ® T является связным тогда и только тогда, когда оно послойно связное.
: f –1(T) ® T является связным тогда и только тогда, когда оно послойно связное.
Рассмотренные здесь свойства будут использованы в следующих пунктах в качестве основы для построения примеров связных и несвязных отображений.
|
из
5.00
|
Обсуждение в статье: Замкнутые отображения. Связь связности и послойной связности |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

