Произведения пространств и проекции

Определение 17. Пусть Х и Y – топологические пространства с топологиями t_Х  и t _Y соответственно. Топологическим произведением этих пространств называется множество X ´ Y с топологией t_{Х ´ Y}, образованной семейством всех множеств вида

U ´ V = ,

и их всевозможных объединений, где U Î t_Х, V Î t _Y  и : X ´ Y ® Х, : X ´ Y ® Y – это проекции, причём (x; y) = x и (x; y) = y. Множества вида U ´ V = называются элементарными (или базисными) открытыми множествами.

Определение 18. Отображение f : X → Y называется открытым, если для каждого открытого множества О Í Х образ f (О) является открытым множеством в Y.

Лемма 2.2. Проекции : X ´ Y ®Х и : X ´ Y ® Y являются непрерывными открытыми отображениями.

Доказательство. Возьмём произвольное открытое в Х множество G. Прообраз этого множества = G ´ Y по определению топологии произведения открыт в X ´ Y. Тогда проекции  и  будут непрерывными отображениями.

 Пусть точка z Î X ´ Y; Oz – её произвольная окрестность (рис.7). Найдётся базисная окрестность

Рис. 7.

Рис. 7.

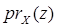точки z, где U – окрестность точки , V – окрестность точки . Точка является внутренней точкой множества U, а значит и множества . Аналогично, точка  – внутренняя точка множества . Следовательно, множества  и  открытые, и проекции  и  – открытые отображения. ÿ

Лемма 2.3. Пусть пространство Х является компактным. Тогда проекция : X ´ Y ® Y является замкнутым отображением.

Доказательство. Возьмём произвольную точку y Î Y и рассмотрим слой = {(x; y): x Î X} = X ´ {y}. Он гомеоморфен множеству Х, поэтому является компактным множеством. Пусть О некоторая окрестность слоя . Рассмотрим произвольную точку z = (x; y) слоя Ì X ´ Y и её элементарную окрестность

G ,

где Ox – окрестность точки x в X, Oy – окрестность точки y в Y. Так как точка z произвольная, следовательно, такими окрестностями можно покрыть всё множество . Пусть  – это открытое покрытие множества 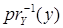. Тогда можно выделить конечное открытое подпокрытие , причём Ì О, которое будем рассматривать как некоторую окрестность слоя . Пусть

U = ,

где О _{i j} = (G_{i j}). Тогда

Í Ì О,

т.е. проекция  является замкнутым над точкой у, и, следовательно, замкнутым отображением. €

Теорема 2.7. Пусть Х связное топологическое пространство. Тогда проекция  : X ´ Y ® Y является связным отображением.

Доказательство. Пусть х – произвольная фиксированная точка пространства Х. Рассмотрим слой 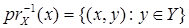= = Y ´ {x}. Он гомеоморфен связному пространству Y, поэтому слой также связен. Предположим, что отображение  несвязное над точкой х, т.е. существует такая окресность Ох точки х, что трубка  является несвязной для всякой окрестности U Í Ox точки x. Зафиксируем некоторую такую связную окрестность U. Для неёнайдутся непустые открытые в  множества О₁ и О₂, что О₁ ∩ О₂ = Æ и О₁ О₂ = . Слой  связен и 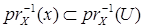, отсюда, по теореме 2.3, содержится либо в О₁, либо в О₂.

Рассмотрим произвольную точку w₁ Î О₁. Образ этой точки = х₁ Ì U. Слой Ì О₁ О₂ = , и точка w₁ принадлежит множеству О₁ и слою , поэтому Ì О₁ (т.к. О₁ ∩ О₂ = Æ). Поскольку w₁ – произвольная точка множества О₁, то 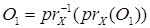. Аналогично, .

Множества О₁  и О₂ дизъюнктные открытые в   и   – открытое отображение. Следовательно, (O₁) и (O₂) – непустые дизъюнктные открытые в U множества и (O₁) (O₂) = U. Отсюда окрестность U несвязная, что противоречит выбору окрестности U. Таким образом, отображение  связное над точкой х и точка х произвольная, поэтому проекция  является связным отображением. €

Следствие 2.5. Если пространства Х и Y связные, то и их произведение X ´ Y является связным множеством.

Доказательство. Предположим обратное. Пусть множество X ´ Y несвязное, т.е. X ´ Y = О₁ О₂, где О₁ и О₂ – непустые дизъюнктные открытые в X ´ Y множества.

Возьмём произвольную точку z Î О₁. Образ этой точки (z) = x. Слой Ì О₁ О₂ связен, и точка х Î О₁, следовательно, Ì О₁ (так как О₁ О₂ = Æ). В силу того, что точка z –  произвольная, получим . Аналогично, . Множества О₁ и О₂ – непустые дизъюнктные открытые в X ´ Y, и отображение  – открытое, следовательно, множества  и  – непустые дизъюнктные открытые в Y и 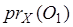= Y. Это противоречит связности Y.

Доказательство можно получить проще. Так как пространство Х связное, то проекция  : X ´ Y ® Y является связным и непрерывным отображением (по теореме 2.7 и лемме 2.2). Пространство Y связное. Тогда, по теореме 2.4, X ´ Y – связное множество. 

Определение 19. Отображение f : X ® Y называется (замкнуто, открыто) параллельно пространству F, если существует такое топологическое вложение i : X ® Y ´ F пространства Х в топологическое произведение Y ´ F, что (множество i(X) соответственно замкнуто, открыто в Y ´ F и)

f = pr_Y 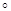i,

где pr_Y : Y ´ F® Y – проекция на сомножитель Y.

Теорема 2.8. Пусть отображение f : X ® Y послойно связное и параллельно пространству F . Тогда отображение f связное.

Доказательство. Отождествим Х с i(X). Тогда f можно отождествить с подотображением проекции pr_Y : Y ´ F® Y. Пусть y Î Y – фиксированная точка и Oy – её произвольная окрестность. Предположим, что для любой связной окрестности U Í Oy точки у трубка f ^–1(U) несвязна. Положим f ^–1(U) = О₁ О₂, где О₁, О₂ – непустые дизъюнктные открытые в f ^–1(U) множества и U Í Oy – некоторая фиксированная связная окрестность точки y.

Пусть х Î f ^–1(y). Тогда х Î О₁ или х Î О₂. Допустим х Î О₁. Найдётся такое открытое в Y ´ F множество G₁, что О₁ = G₁ X. По определению топологии, в Y ´ F найдутся окрестность V_x Í U точки y и открытое в F множество W такие, что

х Î = V_x ´ W Í G₁.

Так как множество f ^–1(y) – связное по условию, то х Î f ^–1(y) Í О₁.

Пусть х ¢ – произвольная точка из (V_x ´ W) Х. Тогда х ¢ Î О₁ и

f ^–1(f (x ¢ )) Í О₁.

Следовательно, О₁ содержит всякий слой f ^–1(y ¢ ), где y ¢ Î V_x (в силу послойной связности f ).

Таким образом, для каждой точки х Î О₁ найдётся окрестность V_x Í U точки f (x), что х Î f ^–1(V_x ) Í О₁. Поэтому

.

Следовательно, множество  является окрестностью точки y и O₁ = f ^–1(V₁). Аналогично устанавливается, что O₂ = f ^–1(V₂), где V₂ непустое открытое в Y множество. Откуда, U = V₁ V₂, что противоречит связности U. Значит, отображение f связное над точкой y. €

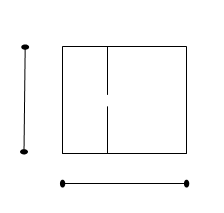
Пример. Если отображение f : X ® Y связное над точкой y, то слой   f ^–1(y) необязательно является связным множеством. Например, пусть f = pr_Y : X ´ Y ® Y – проекция на Y, где Х = Y = [0; 1] (рис. 8). Рассмотрим точку y = Î Y и слой f ^–1(y) над точкой y. Пусть точка z = (x; y) Î X ´ Y, где х = , y = . Тогда слой           f ^–1(y) \ {z} – несвязное множество. Отображение f = pr_Y при этом останется связным, поскольку для любой связной окрестности U точки y трубка f ^–1(U) – линейно связна, следовательно, трубка f ^–1(U) – связна.