Послойное произведение отображений

Определение 20. Пусть f : X ® Y и g : Z ® Y – непрерывные отображения. Послойным произведением f ´ g этих отображений называется отображение h : Т ® Y, где

и

.

Из данного определения вытекает смысл названия такого определения:

для любой точки y Î Y.

Таким образом, в силу следствия 2.5, становится очевидной следующая теорема:

Теорема 2.9. Пусть отображения f : X ® Y  и  g : Z ® Y послойно связные. Тогда произведение h = f ´ g также является послойно связным отображением.

Лемма 2.4. Пусть f, g : X ® Y непрерывные отображения в хаусдорфово пространство Y. Тогда множество Т = {x Î X : f (x) = g(x)} является замкнутым в Х.

Доказательство. Докажем, что множество Х \ Т открытое, т.е. для любой точки x Î X найдётся такая окрестность Ох точки х, что Ох Ì Х \ Т.

Возьмём произвольную точку x Î X \ Т. Тогда f (x) = y₁ Î Y, g(x) = y₂ Î Y. Так как пространство Y хаусдорфово, то существуют окрестности О y₁ точки y₁ и О y₂ точки y₂ такие, что

О y₁ 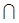О y₂ = Æ.         {*}

Отображения f и g – непрерывные, поэтому множества f ^–1(Oy₁), g^–1(Oy₂) – открытые в Y и x Î f ^–1(Oy₁), x Î g^–1(Oy₂). Рассмотрим окрестность Ох = f ^–1(Oy₁) 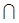g^–1(Oy₂) точки х. Предположим, что Ох 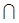Т ≠ Æ, т.е. существует такая точка х₁ Î Ох, что f (x₁) = g (x₁) = y. Но точка y должна принадлежать как окрестности Oy₁, так и окрестности Oy₂, что противоречит условию {*}. ÿ

Лемма 2.5. Если пространства Х и Y компактные, то и их произведение X ´ Y является компактным множеством.

Доказательство. Пусть х – произвольная фиксированная точка пространства Х, и пусть Ω =  – открытое покрытие пространства X ´ Y. Рассмотрим слой

= Y ´ {x}.

Он гомеоморфен связному пространству Y, поэтому 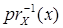 – компактное множество. Тогда из открытого покрытия

Ω(х) = Í Ω,

(где U _a(x) множество, содержащее некоторые точки слоя над точкой x) слоя  можно выбрать конечное открытое подпокрытие ω(х) = . Объединение

U(x) = (x)                        (**)

есть открытое множество, содержащее слой , и pr_X – замкнутое отображение (в силу компактности пространства Y и леммы 2.3). Следовательно, существует такая окрестность Ох точки х, что Í U(x). Семейство {О x: x Î X} образует открытое покрытие пространства X. В силу компактности X, найдется конечное подпокрытие {Ox_i : i = 1,.., k}. Тогда семейство ω =  образует конечное подпокрытие пространства X ´ Y. ÿ

Теорема 2.10. Пусть f : X ® Y  и  g : Z ® Y – связные отображения компактных пространств X и Z в хаусдорфово пространство Y. Тогда произведение h = f ´ g также является связным отображением компактного пространства Т.

Доказательство. По определению послойного произведения,  ( ,  – непрерывные отображения в хаусдорфово пространство Y ) и . Тогда, по лемме 2.4, множество Т является замкнутым в пространстве Х ´ Z, которое, по лемме 2.5, является компактным. Следовательно, множество Т компактно (по теореме 1.7), и его образ h(T) при непрерывном отображении h замкнут в Y (в силу теорем 1.9 и 1.8). Отсюда, отображение h является замкнутым.

Таким образом, в силу теорем 2.9 и 2.3, отображение h = f ´ g является связным. €

Следующая теорема указывает, в каком случае отображения могут быть параллельными пространству Х. Для её доказательства понадобится

Лемма 2.6. Если пространства Х и Y хаусдорфовы, то и их произведение X ´ Y является хаусдорфовым множеством.

Доказательство. Пусть z₁ и z₂ – произвольные фиксированные точки пространства X ´ Y. Рассмотрим точки x₁ = pr_X (z₁), x₂ = pr_X (z₂) и y₁ = pr_Y (z₁), y₂ = pr_Y (z₂) пространств X и Y соответственно. Точки z₁ и z₂ различны, следовательно, x₁ ¹ x₂ или y₁ ¹ y₂. Пусть y₁ ¹ y₂. Тогда, по определению хаусдорфова пространства, в Y существуют такие окрестности Oy₁ и Oy₂ точек y₁ и y₂ соответственно, что Oy₁ 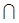Oy₂ = Æ. Проекция pr_Y является непрерывным отображением, поэтому множества  и 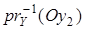 – открытые в X ´ Y и непересекающиеся. Причём, z₁ Î  и z₂ Î . Следовательно, пространство X ´ Y – хаусдорфово по определению. 

Теорема 2.11. Непрерывное отображение f : X ® Y компактного хаусдорфова пространства Х в хаусдорфово пространство Y является замкнуто параллельным пространству Х.

Доказательство. Рассмотрим послойное произведение h = = f ´ i : T ® Y отображений  f : X ® Y и i : Y ® Y, где i – тождественное отображение и множество Т = {(x; y): f pr_X = i pr_Y = pr_Y}. По лемме 2.4, множество Т замкнуто в X ´ Y . Пусть (x₁; y₁) Î T – произвольная фиксированная точка. Тогда pr_Y (x₁; y₁) = y₁ = f pr_X (x₁; y₁). Отсюда, для точек (x₁; y₁), (x₂; y₂) Î Т выполняется неравенство pr_X (x₁; y₁) ¹ pr_X (x₂; y₂) при х₁ ¹ х₂. Следовательно, непрерывное отображение pr_X : Т ® Х биективно. Но пространство T компактно как замкнутое подможество компактного пространства X ´ f (X) Í X ´ Y (в силу теорем 1.7, 1.9 и леммы 2.5). Поэтому отображение g = pr_X : T ® X по следствию 2.1 является гомеоморфизмом, т.е. Т Х, и f = pr_Y . Тогда в качестве топологического вложения можно рассматривать гомеоморфизм d = g^–1: X ® T. Таким образом, множество d(Х) = Т замкнуто в X ´ Y, и f = pr_Y d. Отождествим множества Т и Х с помощью d.. Тогда отображение f замкнуто параллельно пространству Х по определению. 

Литература.

1. Александров П.С. Введение в теорию множеств и общую топологию. – М.: «Наука»,1977.

2. Александров П.С. Геометрия.

3. Вернер А.Л., Кантор Б.Е. Элементы топологии и дифференциальной геометрии. – М.: «Просвещение», 1985.

4. Мусаев Д.К., Пасынков Б.А. О свойствах компактности и полноты топологических пространств и непрерывных отображений. – Ташкент: издательство «Фан» Академии наук республики Узбекистан, 1994.

5. Рубанов И.С. Элементы теоретико-множественной топологии для студентов пединститута. – Киров, 1990.