 |
Главная |
Основное свойство преобразования подобия.
|
из
5.00
|
Преобразование подобия плоскости изменяет расстояние между любыми двумя точками плоскости в одном и том же отношении, равном коэффициенту подобия k, т. е. для любых точек М, N и их образов М', N' выполняется равенство |M / N/|=k 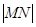 .
.
Доказательство. Пусть относительно Oij точки М и N имеют координаты: М(x1, y1), N(x2, y2). Тогда  =
= 
Образы М' и N' точек М, N имеют соответственно те же координаты (x1, y1), (x2, y2) относительно системы координат O / i / j/. Найдём:
 = =
= =  =
=  =
=  =
=  =
=  , так как
, так как  и
и  .
.
Свойства преобразования подобия.
 Преобразование подобия плоскости всякую прямую отображает в прямую.
Преобразование подобия плоскости всякую прямую отображает в прямую.
 Преобразование подобия плоскости отображает полуплоскость с границей
Преобразование подобия плоскости отображает полуплоскость с границей  в полуплоскость с границей
в полуплоскость с границей  где
где  .
.
 Преобразование подобия плоскости сохраняет простое отношение трёх точек прямой.
Преобразование подобия плоскости сохраняет простое отношение трёх точек прямой.
 Преобразование подобия плоскости сохраняет отношение “лежать между”.
Преобразование подобия плоскости сохраняет отношение “лежать между”.
 Преобразование подобия плоскости отображает угол в равный ему угол.
Преобразование подобия плоскости отображает угол в равный ему угол.
 Преобразование подобия плоскости отображает отрезок в отрезок, луч в луч.
Преобразование подобия плоскости отображает отрезок в отрезок, луч в луч.
 Преобразование подобия плоскости отображает параллельные прямые в параллельные прямые.
Преобразование подобия плоскости отображает параллельные прямые в параллельные прямые.
Следствие. Преобразование подобия плоскости отображает параллелограмм в параллелограмм.
 Преобразование подобия плоскости отображает вектор в вектор, сумму векторов в сумму векторов и произведение числа на вектор в произведение того же числа на соответствующий вектор.
Преобразование подобия плоскости отображает вектор в вектор, сумму векторов в сумму векторов и произведение числа на вектор в произведение того же числа на соответствующий вектор.
Теорема. Если преобразование подобия f с коэффициентом подобия k задано двумя системами координат Oij и O / i / j/, при этом  и O / ( x 0 , y 0 ), то координаты любой точки M ( x , y ) Oij и её образа M / ( x / , y / ) O / i / j / связанысоотношениями:
и O / ( x 0 , y 0 ), то координаты любой точки M ( x , y ) Oij и её образа M / ( x / , y / ) O / i / j / связанысоотношениями:
 где
где  (1)
(1)
Доказательство опирается на определение преобразования подобия, на формулы, связывающие координаты одной и той же точки относительно двух прямоугольных декартовых систем координат, на разложение вектора по базисам.
Замечание. При  системы координат Oij и O / i / j/ одинаково ориентированы, а при
системы координат Oij и O / i / j/ одинаково ориентированы, а при  противоположено ориентированы.
противоположено ориентированы.
Определение. Преобразование подобия плоскости, определяемое формулами (1) называется преобразованием подобия первого рода при  и преобразованием подобия второго рода при
и преобразованием подобия второго рода при  .
.
Из основного свойства преобразования подобия и верного утверждения, обратного ему (если преобразование плоскости изменяет расстояние между точками в одном и том же отношении, равном k>0, то оно является преобразованием подобия с коэффициентом подобия k), следует другое определение преобразования подобия. Определение. Преобразованием подобия плоскости с коэффициентом подобия k>0 называется преобразование плоскости, изменяющее расстояние между любыми точками в одном и том же отношении, равном k.
Гомотетия плоскости.
Определение. Гомотетией плоскости с центром гомотетии О и коэффициентом гомотетии  называется преобразованием плоскости, которое всякой точке М плоскости ставит в соответствии точку М/ по закону
называется преобразованием плоскости, которое всякой точке М плоскости ставит в соответствии точку М/ по закону
 .
.
 Обозначение.
Обозначение.  - гомотетия плоскости с центром гомотетии О и коэффициентом гомотетии k.
- гомотетия плоскости с центром гомотетии О и коэффициентом гомотетии k.
Определение. Гомотетичными называются фигуры  и
и  =
=  .
.
1) Гомотетичные точки М и М/ лежат на одной прямой с центром гомотетии О.
2) Точки М и М/ лежат по одну сторону от центра О, если k>0, и – по разные стороны, если k<0.
3) М / N/= | k|MN.
4) Гомотетия плоскости является при:
k=1-тождественным преобразованием;
k=-1-центральной симметрией.
Формулы гомотетии с центром в начале координат:
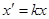 ,
, 
Если центр гомотетии имеет координаты S(x0, y0), то формулы гомотетии с центром S имеют вид:
 ,
, 
Если введем обозначения  ,
,  то получим формулы
то получим формулы
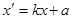 ,
, 
Основное свойство гомотетии.
Для любых точек М, N и их образов 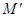 ,
,  имеет место равенство:
имеет место равенство:
 .
.
Доказательство. Воспользуемся равенствами:
 ,
,  ,
,  ,
,  и найдём
и найдём
 .
.
Следствия.
1) Гомотетия с коэффициентом  является преобразованием подобия с коэффициентом подобия
является преобразованием подобия с коэффициентом подобия  , так как из основного свойства следует
, так как из основного свойства следует  или
или  .
.
2)  , если k>0, и
, если k>0, и  , если k<0.
, если k<0.
3) Гомотетия плоскости обладает всеми свойствами преобразования подобия, в частности: прямую отображает в прямую, параллельные прямые - в параллельные прямые, Изменяет все расстояния в одном и том же отношении, сохраняет углы.
Характерные свойства гомотетии.
 Гомотетия плоскости имеет одну неподвижную точку – центр гомотетии.
Гомотетия плоскости имеет одну неподвижную точку – центр гомотетии.
 Гомотетия плоскости отображает прямую, проходящую через центр гомотетии, в себя.
Гомотетия плоскости отображает прямую, проходящую через центр гомотетии, в себя.
 Гомотетия плоскости (
Гомотетия плоскости (  ) отображает прямую, в параллельную ей прямую, так не проходящую через центр гомотетии.
) отображает прямую, в параллельную ей прямую, так не проходящую через центр гомотетии.
 Гомотетия плоскости отображает окружность, центр которой совпадает с центром гомотетии, в концентрическую окружность. При этом радиусы окружностей связаны соотношением
Гомотетия плоскости отображает окружность, центр которой совпадает с центром гомотетии, в концентрическую окружность. При этом радиусы окружностей связаны соотношением  .
.
 Всякие две неравные окружности гомотетичны друг другу, при этом, если окружности не являются концентрическими, существуют две гомотетии, отображающие одну из них в другую.
Всякие две неравные окружности гомотетичны друг другу, при этом, если окружности не являются концентрическими, существуют две гомотетии, отображающие одну из них в другую.






 Гомотетия плоскости является преобразованием подобия первого рода.
Гомотетия плоскости является преобразованием подобия первого рода.
Теорема. Всякое преобразование подобия с коэффициентом подобия k можно представить как композицию гомотетии и движения.
1.5 Группа преобразований подобия и её подгруппы
Теорема 1.Множество всех преобразований подобия плоскости есть группа преобразований, называемая группой подобий.
Доказательство.
 Если
Если 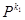 и
и  - преобразования подобия с коэффициентами
- преобразования подобия с коэффициентами  и
и  , то
, то  - преобразования подобия с коэффициентом
- преобразования подобия с коэффициентом  . Действительно
. Действительно  является преобразованием плоскости. Докажем, что для любых двух точек M и N и их образов
является преобразованием плоскости. Докажем, что для любых двух точек M и N и их образов  ,
,  Выполняется равенство
Выполняется равенство  . Обозначим
. Обозначим 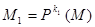 и
и  , тогда
, тогда  ,
,  . По основному свойству преобразования подобия
. По основному свойству преобразования подобия  ,
,  . Поэтому
. Поэтому  и композиция
и композиция  является преобразованием подобия.
является преобразованием подобия.
 Пусть
Пусть  – преобразование подобия плоскости. Так как
– преобразование подобия плоскости. Так как  изменяет всё расстояние в отношение
изменяет всё расстояние в отношение  , то обратное к нему преобразование
, то обратное к нему преобразование 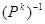 изменяет все расстояния в отношении
изменяет все расстояния в отношении  .
.
Следовательно,  - преобразование подобия с коэффициентом
- преобразование подобия с коэффициентом  .
.
Оба условия  и
и  выполняются. Следовательно, множество всех преобразований подобия является подгруппой группы всех преобразований плоскости, а, значит, и группой.
выполняются. Следовательно, множество всех преобразований подобия является подгруппой группы всех преобразований плоскости, а, значит, и группой.
Определение. Множество всех подобных между собой фигур называется формой.
Теорема 3. Подгруппами группы подобий плоскости являются:
1) Группа преобразований подобия первого рода;
2) Группа движений и все её подгруппы;
3) Группа гомотетий и параллельных переносов;
4) Группа гомотетий с одним и тем же центром.
Метод подобия
Метод подобия оказывается удобным при доказательстве теорем или при решении задач. Этим методом решаются задачи, в которых заданы углы, отношения отрезков и лишь только одно данное условие связано с линейными размерами искомой фигуры. Фигуры, удовлетворяющей всем условиям задачи, кроме того, которое связано с размерами искомой фигуры, подобны между собой. Построив одну из них, а затем, подобрав соответствующим образом, коэффициент подобия, построим искомую фигуру.
Теорема. Медианы треугольника пересекаются в одной точке, каждая медиана делиться этой точкой в отношении 2:1 (считая от вершины треугольника).
Задача. Построить треугольник АВС, если даны:  , отношение сторон АВ:ВС =m:n (m, n-данные отрезки) и медиана к стороне АС.[21]
, отношение сторон АВ:ВС =m:n (m, n-данные отрезки) и медиана к стороне АС.[21]
|
из
5.00
|
Обсуждение в статье: Основное свойство преобразования подобия. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

