 |
Главная |
Использование предложения Паппа на евклидовой плоскости.
|
из
5.00
|
Покажем использование предложения на евклидовой плоскости.
Теорема Паппа: Если А,С,В - три точки на одной прямой, а A’,C’,B’ - на другой, и если три прямые AB’,CA’,BC’ пересекают прямые A’B,C’A,B’C соответственно, то три точки пересечения P,Q,R коллинеарны.

рис. 1
 | |||
 | |||
Доказательство: Эта теорема как и теорема Дезарга использует принадлежность точек прямым или прохождение прямых через точки, без измерения длин или углов и даже без какой-либо ссылки на порядок; в каждом множестве из трех коллинеарных точек безразлично, какая из них лежит между двумя другими. (рис. 1, рис. 2)
 |
рис. 2
 |

 При доказательстве будем пользоваться теоремой Менелая. Предположим, что три прямые AB’,CA’,BC’ образуют треугольник UVW.(рис. 3)
При доказательстве будем пользоваться теоремой Менелая. Предположим, что три прямые AB’,CA’,BC’ образуют треугольник UVW.(рис. 3)

рис. 3
 |
Применяя теорему Менелая к пяти тройкам точек
íP,A’,Bý, íA,Q,C’ý, íB’,C,Rý, íA,C,Вý, íB’,A’,C’ý,
лежащих на сторонах этого треугольника, мы получаем.
(VP/WP)*(WA’/UA’)*(UB/VB)=1 (VA/WA)*(WC/UC)*(UB/VB)=1
(VB’/WB’)*(WC/UC)*(UR/VR)=1 VB'/WB')*(WA'/UA')*(UC'/VC')=1
(VA/WA)*(WQ/UQ)*(UC’/VC’)=1
Разделив произведение первых трех соотношений на произведение последних двух, производя сокращение, мы получаем:
(VP/WP)*(WQ/UQ)*(UR/VR)=1
то есть P,Q,R коллинеарны, теорема доказана.
Приложение
№1. Если два треугольника перспективны относительно точки и две пары соответствующих сторон параллельны, то и две оставшиеся стороны параллельны.


 Дано: треугольник PRQ и треугольник P’R’Q’ перспективны относительно точки О. QR||Q’R’, PR||P’R’
Дано: треугольник PRQ и треугольник P’R’Q’ перспективны относительно точки О. QR||Q’R’, PR||P’R’
Доказать что: QP||Q’P’
Доказательство:

 Так как QR||Q’R’ и RP||R’P’, то
Так как QR||Q’R’ и RP||R’P’, то
 | |||
 | |||
(OQ/OQ’)=(OR/OR’)=(OP/OP’) Þ (OQ/OQ’)=(OP/OP’) Þ QP||Q’P’
№2.Назовите два треугольника перспективных относительно:

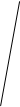 а) точки Р
а) точки Р



 б) точки Р’
б) точки Р’
 в) точки D
в) точки D
 |
Ответы: а) треугольники ROQ и EP’F б) треугольники EFP и R’Q’O’ в) треугольники R’RE и Q’QF.






 №3. Если А,С,Е - три точки на одной прямой, B,D,F- на другой, и если прямые АВ и CD параллельны прямым DE и FA соответственно, то прямые EF||BC.
№3. Если А,С,Е - три точки на одной прямой, B,D,F- на другой, и если прямые АВ и CD параллельны прямым DE и FA соответственно, то прямые EF||BC.
 |
1) АС||BD. Рассмотрим параллелограмм ABDE и AFDC Þ BD=AE и DF=AC. Произведем вычитание BD-DF=BF; AE-AC=CE Þ BF=CE Þ BCEF - параллелограмм Þ EF||BC.
 |
2)
3) ACÇBD=0, так как AB||ED и CD||FA, то (|OA|/|OB|)=(|OE|/|OD|) и (|OC|/|OD|)=(|OA|/|OF|) получаем |OB|*|OE|=|OA|*|OD|=|OC|*|OF| Þ
(|OE|/|OF|)=(|OC|/|OB|) Þ EF||CB.
№4. Пусть A,B,D,E,N,M - шесть точек, обладающих тем свойством, что прямые AE,DM,NB пересекаются в одной точке и прямые АМ,DB,NE пересекаются в одной точке. Что можно сказать о прямых AB,DE,NM?
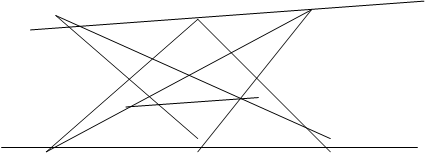 |
Решение. Пусть AEÇDMÇNB=C, AMÇDBÇNE=F обозначим () пересечения прямых АВ и DE через L. По теореме Паппа ()LÎMN Þ ABÇDEÇMN=L. Прямые AB,DE,NM пересекаются в одной точке.
№5. Доказать, что медианы треугольника пересекаются в одной точке.
AA’ÇBB’ÇCC’=S ?
Решение: Рассмотрим треугольник АВС и треугольник А1В1С1- дезарговые треугольники, то есть треугольники удовлетворяют теореме Дезарга.
 | |||
 | |||
ABÇ А1В1=P¥
BCÇ В1С1=Q¥
ACÇ А1С1=R¥
 |
лежат на одной несобственной прямой S¥
по обратной теореме Дезарга прямые, проходящие через соответствующие вершины, пересекаются в одной точке S.
AA’ÇBB’ÇCC’=S.


 №6. В евклидовой плоскости в четырехугольник вписана трапеция, параллельные стороны которой || его диагонали. Доказать, что непараллельные стороны трапеции пересекаются на другой диагонали.
№6. В евклидовой плоскости в четырехугольник вписана трапеция, параллельные стороны которой || его диагонали. Доказать, что непараллельные стороны трапеции пересекаются на другой диагонали.
 |
Решение: треугольники NCK и AMP дезарговые треугольники по прямой теореме Дезарга, соответствующие стороны этих треугольников пересекаются в ()-ах, лежащих на одной прямой Þ ()F,D,B, то есть () пересечения непараллельных сторон трапеции принадлежат диагонали BD.
№7. В евклидовой плоскости противоположные вершины одного параллелограмма расположены соответственно на противоположных сторонах второго. Доказать, что оба параллелограмма имеют общий центр симметрии.



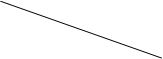



 Требуется доказать, что LNÇMKÇBDÇAC=S
Требуется доказать, что LNÇMKÇBDÇAC=S
Решение.
 |
ACÇLNÇBD - треугольники ALD и СNB - дезарговые треугольники удовлетворяют обратной теореме Дезарга Þ ACÇLNÇBD=S.
Треугольники DKC и BMA - дезарговые треугольники по обратной теореме Дезарга Þ MKÇBDÇAC=S
Получили ACÇBDÇMKÇLN=S.
Оба параллелограмма имеют общий центр симметрии.
№8. В евклидовой плоскости дан треугольник и три параллелограмма, для каждого из которых одна сторона треугольника служит диагональю, а две другие - смежными сторонами. Доказать, что вторые диагонали этих параллелограммов пересекаются в одной точке.
Требуется доказать, что ANÇBPÇCM=S.


 Решение: Треугольники ABC и NPM - дезарговые треугольники.
Решение: Треугольники ABC и NPM - дезарговые треугольники.
 | |||
 | |||
ABÇNP=Q¥
 BCÇMP=R¥
BCÇMP=R¥
ACÇNM=K¥
лежат на одной несобственной прямой P¥
по теореме обратной теореме Дезарга NAÇBPÇCM=S.
№9. В треугольнике АВС из его вершин проведены прямые, пересекающиеся в одной () S; A’=ASÇBC, B’=BSÇAC, C’=CSÇAB. Доказать, что точки BCÇB’C’, ACÇA’C’, ABÇA’B’ лежат на одной прямой.


 Решение.
Решение.
 |
Обозначим () пересечения сторон BCÇB’C’, ACÇA’C’, ABÇA’B’ соответственно P,R,Q. Рассмотрим треугольники АВС и А’В’С’ прямые проходящие через вершины этих треугольников пересекаются в () SÞ () пересечения соответствующих сторон P,R,Q лежат на одной прямой.







 №10. В конфигурации Дезарга одну из точек выбрать за дезаргову точку. Найти в этой конфигурации вершины дезарговых треугольников и дезаргову прямую.
№10. В конфигурации Дезарга одну из точек выбрать за дезаргову точку. Найти в этой конфигурации вершины дезарговых треугольников и дезаргову прямую.
 |
Точка А- дезаргова точка
Треугольники A’RP и SCB - дезарговы треугольники
A’®S SCÇA’R=C’
R®C SBÇA’P=B’
P®B CBÇRP=Q.
Точки C’,B’,QÎS - дезаргова прямая.
№11. Сформулировать в терминах евклидовой геометрии теорему Дезарга для случая:
1) ()S¥ - несобственная (), дезаргова прямая S - собственная.
 |
Формулировка теоремы Дезарга: Если прямые проходящие через соответствующие вершины двух треугольников параллельны, то точки пересечения соответствующих сторон лежат на одной прямой.
2) ()S собственная, прямая S¥ - несобственная.
Формулировка.







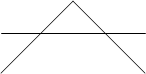
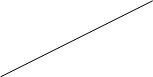 Если прямые, походящие через соответствующие вершины двух треугольников АВС и А’В’С’ пересекаются в одной точке и AB||A’B’, B’C||BC, то AC||A’C’.
Если прямые, походящие через соответствующие вершины двух треугольников АВС и А’В’С’ пересекаются в одной точке и AB||A’B’, B’C||BC, то AC||A’C’.
 | |||
 | |||
 | |||
3) ()S¥ - несобственная, прямая S¥ - несобственная.
Формулировка.
Если прямые проходящие через соответствующие вершины двух треугольников параллельны и AB||A’B’, BC||B’C’, то AC||A’C’.
№12. Прямая p лежит в плоскости треугольника АВС; К=ВСÇp, L=ACÇp, M=ABÇp, R=BLÇCM, S=CMÇAK, T=AKÇBL.



 Доказать, что прямые AR,BS и CT пересекаются в одной точке.
Доказать, что прямые AR,BS и CT пересекаются в одной точке.
Требуется доказать, что ARÇBSÇCT=Q
 |
Решение
 Треугольники АВС и RST - дезарговы треугольники.
Треугольники АВС и RST - дезарговы треугольники.
RSÇAB=M
TSÇBC=K () M,K,LÎз (по условию)
TRÇAC=L
Таким образом, по теореме обратной теореме Дезарга ARÇBSÇCT=Q.
 №13. Даны прямые a и b, пересекающиеся в точке S, которая лежит за пределами чертежа. Дана ()С не лежащая ни на одной из данных прямых. Построить прямую SC.
№13. Даны прямые a и b, пересекающиеся в точке S, которая лежит за пределами чертежа. Дана ()С не лежащая ни на одной из данных прямых. Построить прямую SC.




 Построение.
Построение.
 |
Выбираем произвольно прямую s, () A,A’Îa и ()ВÎb.
1)ABÇs=P, 2)PA’Çb=B’, 3)ACÇs=R,
4)BCÇs=Q, 5)A’R, B’Q, 6)B’QÇA’R=C’,
7)CC’ искомая прямая.
Доказательство:
 Треугольники АВС и А’В’С’ - дезарговы треугольники, прямая s - дезаргова прямая.
Треугольники АВС и А’В’С’ - дезарговы треугольники, прямая s - дезаргова прямая.
ABÇA’B’=P
ACÇA’C’=R Îs (по построению)
BCÇB’C’=Q
По обратной теореме Дезарга AA’ÇCC’ÇBB’=S.
№14. Даны две точки P и Q и не проходящая через них прямая c. построить () PQÇC, не проводя PQ.
Анализ: Произвольно выбираем прямую s, ()Q1ÎC,Q
QQ1Q2 - трехвершинник, построить РР1Р2 – трехвершинник,P1ÎC, PQÇP1Q1ÇP2Q2=S


 Обратная теорема Дезарга.
Обратная теорема Дезарга.

 Построение:
Построение:
1) 
 QQ1Çs=X
QQ1Çs=X
2)  PXÇC=P1
PXÇC=P1
3) Q1Q2Çs=Y
4) QQ2Çs=Z
5)  YP1
YP1
6) ZPÇYP1=P2
7) P2Q2Çc=S ()S - искомая точка.
Доказательство:
Треугольники QQ1Q2 и PP1P2 - дезарговы.
 QQ2ÇPP2=Z
QQ2ÇPP2=Z
QQ1ÇPP1=X ÎS (по построению).
Q1Q2ÇP1P2=Y
По обратной теореме Дезарга. PQÇP1Q1ÇP2Q2=S Þ PQÇc=S искомая точка.
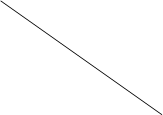
№15. На евклидовой плоскости даны две параллельные прямые a||b и точка С, им не принадлежащая. Через () С провести прямую, параллельную а и b.
1) Анализ: Произвольно выбираем прямую s. ()А,А’Îа, ()ВÎb.
Здесь работает обратная теорема Дезарга для случая ()S¥ - несобственная, прямая s - собственная.
Треугольники АВС и А’В’С’ - построить.
2)
|



 Построение:
Построение:
|
|

 1)АВÇs=P
1)АВÇs=P
|
|
 2) A’PÇb=B’
2) A’PÇb=B’
|
|
 3) ACÇs=R
3) ACÇs=R
|
|

 4) BCÇs=Q
4) BCÇs=Q
5) A’R, B’Q
|
|
7) CC’ - искомая прямая.
|
Треугольники АВС и А’В’С’- дезарговы
Формулировка обратной теоремы Дезарга.
Если прямые, содержащие соответственные стороны треугольников АВС и А’В’С’ пересекаются в точках лежащих на одной прямой и АА’||BB’, то СС’||AA’.
По этой теореме СС’- искомая прямая.
№18. Трапеция ABCD пересечена прямыми p и q, параллельными основанию АВ, pÇAD=M, pÇAC=P, qÇBD=N, qÇBC=Q. Доказать, что точка MNÇPQ лежит на прямой АВ.
 Требуется доказать, что MNÇPQÇAB=K.
Требуется доказать, что MNÇPQÇAB=K.
Решение:
Рассмотрим треугольники
МРА и NQB.
МРÇNQ=S¥, так как p||q. (pÇq=S¥)
PAÇBQ=C
AMÇBN=D
DC||p||q Þ DCÇpÇq=S¥ Þ C,D,S¥Î одной прямой по теореме обратной теореме Дезарга MNÇPQÇAB=K.
Тем самым доказали, что точка МNÇPQÎAB.
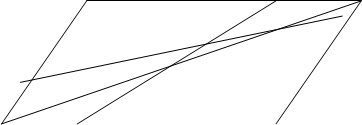
№17. В евклидовой плоскости даны параллелограмм АВСD, ()РÎCD и прямая l пересекающая стороны АВ и АD. Провести прямую || l.
1)  Анализ: Треугольник ANM построен. Построить треугольник СРК. Задача решается с помощью прямой теоремы Дезарга.
Анализ: Треугольник ANM построен. Построить треугольник СРК. Задача решается с помощью прямой теоремы Дезарга.
 |
2) Построение:
1)  NP, AC
NP, AC
2)  NPÇAC=S
NPÇAC=S
3) MSÇBC=K
4) KP- искомая прямая.
3) Доказательство:
треугольники ANM и CPK - дезарговы, так как ANÇCP=R¥ (AN||CP), CKÇAM=Q¥ (CK||AM) то по теореме Дезарга KPÇNM=F¥ Þ KP||NM.
Список литературы
1. Р. Хартсхорн “Основы проективной геометрии”.-М:Мир,1970.
2. Ефимов “Высшая геометрия”-:Наука,1971.
3. Франгулов С.А. “Лекции по проективной геометрии”-Л:ЛГПИ,1975.
4. Вахмянина О.А., Измайлова Т.С. “Пособие по проективной геометрии”-Оренбург:ОГПИ,1994.
5. Коксетер С.М. “Новые встречи с геометрией”-М:Нуака,1978
6. Базылев “Геометрия”-М:Просвещение,1975
7. Потоцкий “Что изучает проективная геометрия ”-М: Просвещение,1982
8. Певзнер “Проективная геометрия”-М:Просвещение,1980
9. Измайлова Т.С. Лекционный курс по проективной геометрии.
|
из
5.00
|
Обсуждение в статье: Использование предложения Паппа на евклидовой плоскости. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

