Аксиома Паппа и основная теорема о проективных преобразованиях прямой.

Докажем “основную теорему”, которая утверждает, что существует единственное проективное преобразование прямой, переводящее три заданные точки в любые другие три заданные точки. Эта теорема не следует из аксиом П1-П5 и П7; поэтому нам предстоит дополнительно ввести аксиому Паппа П6.

Основная теорема (теорема о проективных преобразованиях прямой). Пусть задана прямая l и А,В,С;A’,B’,C’- две тройки различных точек этой прямой. Тогда существует одно и только одно проективное преобразование l, такое, что АВС - A’B’C’.

П6 (аксиома Паппа). Пусть l и l’-две различные прямые, А,В,С- три различные точки прямой l, отличные от Х=lÇl’и А’,В’,С’- три различные точки прямой l’, отличные от Х. Тогда точки P=AB’ÇA’B, Q=AC’ÇA’C, R=BC’ÇB’C коллинеарны.

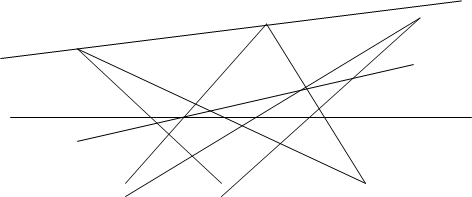
Предложение 1: Аксиома П6 влечет за собой двойственную аксиому Паппа П6*, то есть принцип двойственности применим и ко всем выводам из П6.

Предложение 2: На действительной проективной плоскости справедлива аксиома П6.

Лемма 1: Пусть l = m = n, где l¹n, предположим еще, что или:

а)прямые l, m, n принадлежат одному пучку, или

б)точки O,P и lÇn коллинеарны.

Тогда полученное проективное отображение l - n является перспективным (то есть $ такая точка Q, что перспективное отображение l = n совпадает с нашими проективными отображениями l - n).

Лемма 2: Пусть l = m = n,

Где l¹n; предположим теперь, что не имеет места ни а) ни б) из условий леммы 1. Тогда $ прямая m’ и точки O’În и P’Îl, такие, что l = m = n есть рассматриваемое проективное отображение l на n.

Доказательство: Пусть l, m, n, O,P заданы; пусть далее A,A’- две точки на l и AA’ = BB’ = CC’. Точку пересечения ОР и n обозначим через O’. Так как мы предположили, что точки О,Р, lÇn=X неколлинеарны, то O’¹X, то есть O’Ïl. Проведем O’A и O’A’; пусть они пересекаются РС и РС’ соответственно в D и D’.

Соответствующие стороны треугольников АBD и A’B’D’ пересекаются в коллинеарных точках O,P,O’; значит, по П5*, прямые, соединяющие соответственные вершины этих треугольников принадлежат одному пучку. Таким образом, прямая m1, содержащая D и D’, проходит через точку Y=lÇm.

Следовательно, прямая m1 определена точками D и Y, и если точка A’ меняется, то D’ меняется, оставаясь на прямой m1. Поэтому исходное проективное отображение совпадает с отображением l = m1 = n.

Повторяя то же самое рассуждение еще раз, мы можем переместить Р в положение P’=OPÇl и найти новую прямую m’, такую, что l = m’= n дает исходное проективное отображение.

Лемма 3: Пусть l и l’- две различные прямые. Тогда любое проективное отображение l - l’ может быть получено как композиция двух перспективных отображений.

Теорема 1: Основная теорема вытекает из аксиом П1-П6.

Доказательство: Для заданной прямой l и двух троек различных точек А,В,С и A’,B’,C’ этой прямой мы должны найти проективное преобразование, переводящее одну тройку в другую, и доказать, что оно единственно. Выбираем прямую l’, не проходящую через заданные точки, и спроектируем A’,B’,C’ на l’. Обозначим образы этих точек теми же буквами A’,B’,C’. Таким образом мы свели теорему к следующей: имеем А,В,С на l A’,B’,C’ на l’ (все точки отличны от lÇl’) требуется показать, что $ единственное проективное отображение, такое, что ABC - A’B’C’. Одно такое проективное отображение мы уже получили в предложении 2 (п.3.7); следовательно, достаточно показать, что любое другое проективное отображение совпадает с этим.

Случай 1: Предположим, что второе проективное отображение есть просто перспективное отображение. Пусть l - l’ переводит ABC = A’B’C’. Рассмотрим P=AB’ÇA’B ; пусть прямая l’’ соединяет Р с Q. Мы утверждаем, что l’’ проходит через точку Х=lÇl’. Действительно, применим П5 к треугольникам AB’C’ и A’BC, которые перспективны с центром О. Их стороны пересекаются в точках Р,Q,Х соответственно. Следовательно, l’’ определяется точками Р и Х.

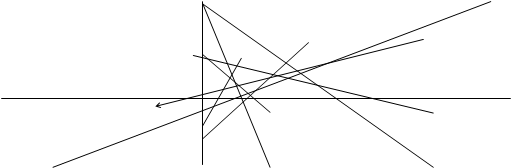Но так как С может меняться, перспективное отображение l = l’ совпадает с проективным отображением l = l’’ = l’

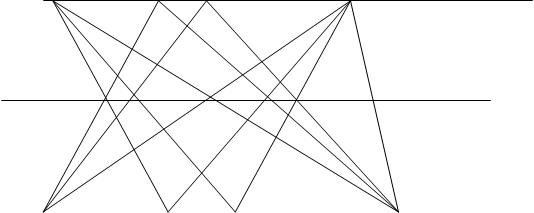
Случай 2: предположим, что второе проективное отображение не является перспективным. Тогда в силу леммы 3 оно может быть представлено в виде композиции двух перспективных отображений, а в силу леммы 2 можно предположить, что центры этих отображений принадлежат соответственно l ’ и l. Таким образом, мы приходим к конфигурации: l = l’’ = l’ и ABC = A’’B’’C’’ = A’B’C’

Применяя П6 к треугольникам АBR и A’B’R’, мы получаем, что Р=АB’ÇA’BÎl’’. Аналогично, применяя П6 к ACR и A’C’R’, мы получаем, что Q=AC’ÇA’CÎl’’. Таким образом, l’’ есть прямая, которая была использована в предложении 2 (п.3.7) для построения второго проективного отображения

l = l’’ = l’

Пусть теперь DÎl – произвольная точка; определим D’’=R’DÇl’’и D’=RD’’Çl’.

Из П6, применимой к треугольникам ADR и A’D’R’, следует, что AD’ÇA'D, A’’,D’’ коллинеарны, то есть AD’ÇA’DÎl’’. Но это означает, что также и проективное отображение предложения 2 переводит D в D’. Следовательно, эти проективные отображений совпадают.          ч.т.д.

Теорема 2: П5 следует из П6.

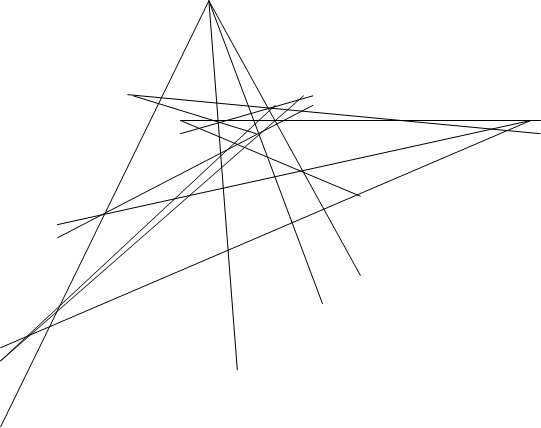
Доказательство: Пусть, О,A,B,C,A',B',C' удовлетворяют предложениям теоремы Дезарга (П5), построим P,Q,R. Для доказательства их коллинеарности нам придется трижды применить П6.

Шаг 1: Пусть A’C’ пересекает АВ в точке S. Затем применим П6 к прямым.

О С C’    

B S A   и заключим отсюда, что точки T=OSÇBC, U=OAÇBC’, Q коллинеарны.

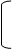Шаг 2: Применим теперь П6 к тройкам            O B B’    

                                                               C’ A’ S

и заключим отсюда, что точки U,V=OSÇB’C’, P коллинеарны.

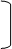
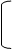Шаг 3: Применим, наконец, П6 к тройкам B C’ U

                                                               V T S

и заключим отсюда, что точки R, P=BSÇUV (шаг2),Q=C’SÇTU (шаг1) коллинеарны. ч.т.д.

Следствие: (из основной теоремы). Проективное отображение l - l’, где l¹l’, есть перспективное отображение Û точка пересечения X=lÇl’ переходит в себя.

Глава 4. Применение основных теорем к решению задач на евклидовой плоскости.