Комплексные числа и операции над ними.

Первообразная. Неопределённый интеграл. Таблица основных интегралов. Основные свойства неопределённого интеграла.

Функция F(х) называется первообразной функции f(x) на интервале (а; Ь), если для любого х ϵ (а; Ь) выполняется равенство F '(х) = f(x) (или dF(x) = f(x) dx).

Теорема 29.1. Если функция F(х) является первообразной функции f(x) на (а; Ь), то множество всех первообразных для f(x) задается формулой F (х) + с, где С – постоянное число.
Множество всех первообразных функций F(x) + С для f(x) называется неопределенным интегралом от функции f(x) и обозначается символом . Таким образом, по определению = F(x) +C .
Свойства неопределенного интеграла

1. Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна
подынтегральной функции: d( ) = f(x) dx, ( )’ = f(x).
2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: 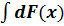= F(х) + С.
3.Постоянный множитель можно выносить за знак интеграл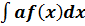а: = а* , а≠0 - постоянная.
4.Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций: = ± .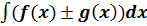
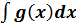5. (Инвариантность формулы интегрирования). Если  = F(x) + C, то и 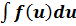 = F(u) + C, где u = ϕ(х) - произвольная функция, имеющая непрерывную производную.

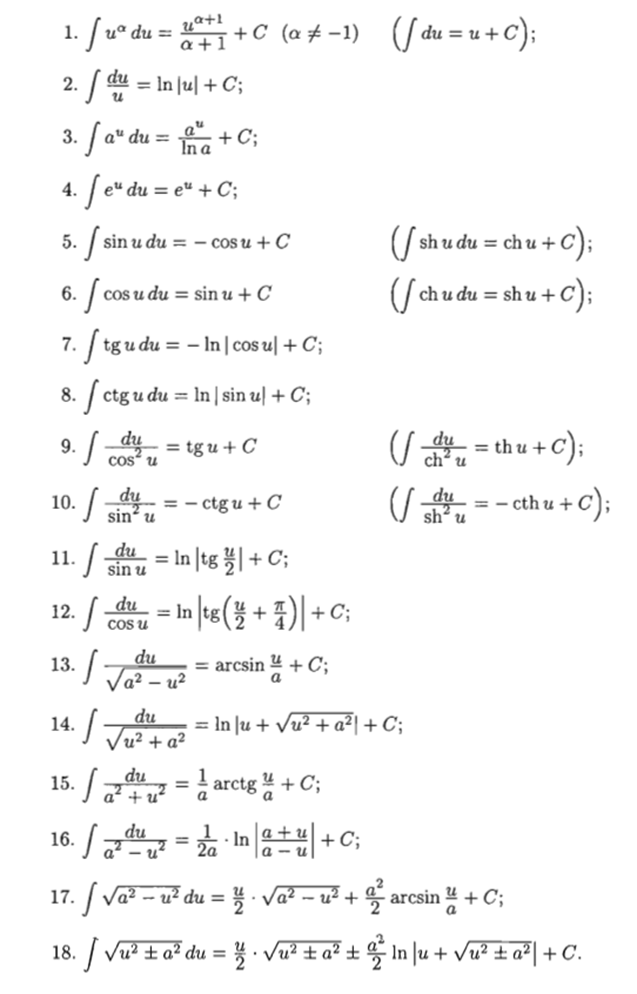2. Метод замены переменной в неопределённом интеграле. Метод интегрирования по частям.

Метод интегрирования подстановкой заключается во введении но­ вой переменной интегрирования (т. е. подстановки).
Пусть требуется вычислить интеграл . Сделаем подстановку х = φ(t), где φ(t) - функция, имеющая непрерывную производную. Тогда dx = φ'(t)dt и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой. = 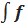( φ ( t )) * φ '( t ) dt
Иногда целесообразно подбирать подстановку в виде t = φ(х), тогда 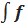(φ( x )) *φ'(х) dx = , где t = φ(х).

Пусть u = u(х) и v = v(x) - функции, имеющие непрерывные производные. Тогда d( uv) = u*dv + v*du. Интегрируя это равенство, получим
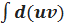= +  или = uv -
Полученная формула называется формулой интегрирования по частям.
Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.
1. Интегралы вида dx, 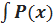*sinkxdx, 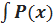*coskxdx, где Р(х) - многочлен, k - число. Удобно положить u = Р(х), а за dv обозначить все остальные сомножители.
2. Интегралы вида 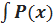arcsinxdx, 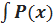arccosxdx, / P(x)lnxdx, / P(x)arctgxdx, / P(x)arcctgxdx. Удобно положить Р(х) dx = dv, а за u обозначить остальные сомножители.
3. Интегралы вида *sinbхdx, *cosbхdx, где а и b - числа. За u можно принять функцию u = е^ax.

Комплексные числа и операции над ними.

Комплексным числом z называется пара (x, y) действительных чисел x и y. При этом равенство, сумма и произведение упорядоченных пар, а также отождествление некоторых из них с действительными числами определяются следующим образом:
1) два комплексных числа z₁ = (x₁, y₁) и z₂ = (x₂, y₂) называются равными, если x₁ = x₂ и y₁ = y₂;
2) суммой комплексных чисел z₁ и z₂ называется комплексное число z вида
z = (x₁ + x₂, y₁ + y₂);
3) произведением комплексных чисел z₁ и z₂ называется комплексное число z = (x₁x₂ - y₁y₂, x₁y₂ + x₂y₁);
4) множество комплексных чисел (x,0), xϵR, отождествляется с множеством действительных чисел R.
Разностью комплексных чисел z₁ и z₂ называется комплексное число z такое, что z₂ + z = z₁, откуда находим z = z₁ - z₂ = (x₁ - x₂, y₁ - y₂).
Частным комплексных чисел z₁ и z₂ называется комплексное число z такое, что *z= . Отсюда находим

Комплексное число (0, 1) обозначается символом i = (0, 1). Тогда (0,1)*(0,1)=(-1,0) т. е. i ² = -1. Произвольное комплексное число z можно записать в виде z = ( x , y ) = ( x , 0) + (0, y ) = ( x , 0) + (0, 1)( y , 0) = x + iy .
Эта запись называется алгебраической формой комплексного числа. Комплексное число =( x ,- y )= x - iy называется сопряженным по отношению к комплексному числу z = ( x , y ) = x + iy .

4. Основная теорема алгебры. Разложение многочленов с действительными коэффициентами на линейные и квадратичные множители.

Основная теорема алгебры. Всякий многочлен, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный.
Выражения вида a 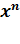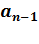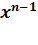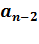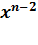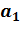( x )= * + * + * +….+ * x + 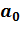 называются многочленами от х степени n ( ≠0) c действительными коэффициентами, если , i =0,1,2,…, n – действительные числа.
Как известно, если комплексное число = g + ih – корень многочлена, то обязательно и комплексно сопряженное ему число = g - ih является корнем многочлена. Поэтому их произведение (х- )*( x - )=( x - g - ih )*( x - g + ih )= 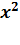-2 gx + 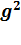+  представляет собой квадратичное выражение.
Таким образом, любой многочлен с действительными коэффициентами всегда можно представить в виде произведения линейных и квадратичных множителей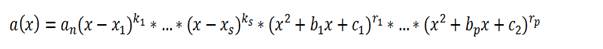

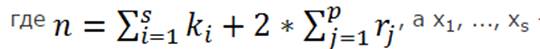
- действительные корни многочлена. То есть, если известны все корни многочлена с действительными коэффициентами, то можно сразу написать его разложение на множители.

5. Рациональные дроби. Интегрирование элементарных рациональных дробей. Разложение правильной рациональной дроби на сумму простейших.

Дробно-рациональной функцией (или рациональной дробью) называется функция, равная отношению двух многочленов, т. е. f(x) = 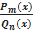, где (х) - многочлен степени m, а Qn(x) - многочлен степени n.
Рациональная дробь называется правильной, если степень числителя меньше степени знаменателя, т.е. m < n; в противном случае (если m ≥n) рациональная дробь называется неправильной.
Всякую неправильную рациональную дробь 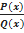 можнo, путем деления числителя на знаменатель, представить в виде суммы многочлена L(x) и правильной рациональной дроби  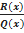, т.е. 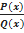= L ( x )+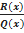
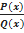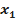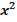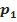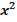Всякую правильную рациональную дробь  знаменатель которой разложен на множители Q ( x ) = (х -  )^ k 1 * (х - )^ k 2 *… *( + x + )^ s 1*…*(  + x + 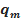)^s m , можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:
где 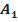, , …, , , 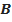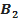…, , , 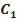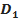…, , … - некоторые действительные коэффициенты.
Рассмотренный материал позволяет сформулировать общее правило интегрирования рациональных дробей.
1. Если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби; 2. Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей; 3. Проинтегрировать многочлен и полученную сумму простейших дробей.

6.Интегрирование функций вида. Интегрирование дифференциальных биномов

Интегралы типа  (х, ( ax + b /сх + d)^ m / n , ... ,( ax + b /сх + d)^ r / s ) dx, где а, b, c, d - действительные числа, a m, n, ... , r, s - натуральные числа, сводятся к интегралам от рациональной функции путем подстановки ах + b/cx+d= t^k , где k - наименьшее общее кратное знаменателей дробей m / n , r / s .

Интегралы типа * a + b 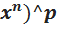dx (называемые интегралами от дифференциального бинома), где а, b - действительные числа; m, n, р - рациональные числа, берутся, как показал Чебышев П.А., лишь в случае, когда хотя бы одно из чисел р, (m+1/n) или ( m +1/ n )+ p является целым. Рационализация интеграла в этих случаях осуществляется следующими подстановками: 1) если р - целое число, то подстановка х = t^k , где k - наименьшее общее кратное знаменателей дробей m и n; 2) если (m+1/ n ) - целое число, то подстановка а + bх^n = t^s , где s - знаменатель дроби р; 3) если ((m + 1)/ n ) + р - целое число, то подстановка а + bх^n = х^n*t^s , где s - знаменатель дроби р. Во всех остальных случаях интегралы типа / х^m(а + bх^n)^ p dx не выражаются через известные элементарные функции, т. е. «не берутся».