Дифференциальные уравнения с разделяющимися переменными, однородные и приводящиеся к ним

Наиболее простым ДУ первого порядка является, уравнение вида
Р(х) * dx + Q(y) *dy = 0. (48.5)
в нем одно слагаемое зависит только от х, а другое - от у. Иногда такие ДУ называют уравнениями с разделёнными переменными. Проинтегрировав почленно это уравнение, получаем:
 +  = С - его общий интеграл.
Более общий случай описывают уравнения с разделяющимися переменными, которые имеют вид
Особенность уравнения (48.6) в том, что коэффициенты при dx и dy представляют собой произведения двух функций (чисел), одна из которых зависит только от х, другая - только от у. Уравнение (48.6) легко сводится к уравнению (48.5) путем почленного деления его на (y) * (х) ≠ 0. Получаем:

- общий интеграл.

Замечание 1. При проведении почленного деления ДУ на  (у)x  (х) могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнение Q1 (у) *P2(х) = 0 И установить те решения ДУ, которые не могут быть получены из общего решения - особые решения.
2. Уравнение y ' = (Х) * f2(Y) также сводится к уравнению с разделенными переменными. Для этого достаточно положить у' = dy /dx и разделить переменные.
З. Уравнение y' = f(ax + Ьу + с), где а, Ь, с - числа, путем замены ах + bу + с = u сводится к ДУ с разделяющимися переменными.
Дифференцируя по х, получаем:

откуда следует

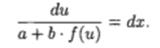
Интегрируя это уравнение и заменяя и на ах + bу + с, получим общий интеграл исходного уравнения.
Однородные дифференциальные уравнения
К уравнению с разделяющимися переменными приводятся однородные ДУ первого порядка.
Функция f(x; у) называется однородной функцией n-го nорядка (измеренuя), если при умножении каждого ее аргумента на про извольный множитель λ вся функция умножится на 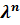, т. е. f (λ* x ;λ* y )= 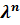* f ( x ; y ).
Например, функция f(x; у) = 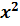 - 2ху есть однородная функция второго порядка, поскольку

Дифференциальное уравнение у' = f(x;y) (48.7)
Называется однородным, если функция f(x; у) есть однородная функция нулевого порядка.
Покажем, что однородное ДУ (48.7) можно записать в виде y ’= ϕ ( y / x ) (48.8)
 Если f(x; у) - однородная функция нулевого порядка, то, по определению, f(x; у) = f(λx; λу). Положив λ= 1/ x , получаем:

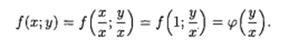
Однородное уравнение (48.8) преобразуется в уравнение с разделяющимися переменными при помощи замены переменной (подстановки) y/x=u или, что то же самое, у = u* x (48.9)
Действительно, подставив у = uх и у' = u'х + u в уравнение (48.8), получаем u'х+u = ϕ( u ) или x* du / dx = ϕ(u)-u, т. е. уравнение с разделяющимися переменными. Найдя его общее решение (или общий интеграл), следует заменить в нем u на y/x. Получим общее решение (интеграл) исходного уравнения.
Однородное уравнение часто задается в дифференциальной форме:
P ( x ; y )* dx + Q ( x ; y )* dy = 0 (48.10)
ДУ (48.10) будет однородным, если P(x;y) и Q(x;y) – однородные функции одинакового порядка.
Переписав уравнение (48.10) в виде dy/dx= - и применив в правой части рассмотренное выше преобразование, получим уравнение у' = ϕ(y/x).
При интегрировании уравнений вида (48.10) нет необходимости предварительно приводить их (но можно) к виду (48.8): подстановка (48.9) сразу преобразует уравнение (48.10) в уравнение с разделяющимися переменными.