Геометрический и физический смысл определённого интеграла.

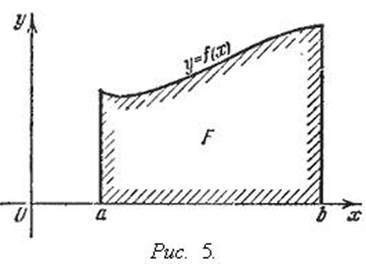
Геометрический смысл определенного интеграла. Если f ( x ) непрерывна и положительна на [ a , b ], то интеграл 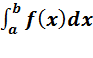представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a , x = b , y = f ( x ) (см. рис. 5.).

Физический смысл определенного интеграла: пусть материальная точка M движется вдоль числовой оси со скоростью V ( t ), V ( t )≥0 . Тогда путь, пройденный точкой за промежуток времени от t = a до t = b , равен определенному интегралу от скорости: S =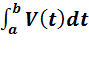

Замена переменной в определённом интеграле.

Пусть для вычисления интеграла 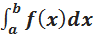 от непрерывной функции сделана подстановка х = φ(t).
Теорема 1. Если: 1) функция х = φ(t) и ее производная х' =φ’(t) непрерывны при t ϵ [α;β]; 2) множеством значений функции х = φ(t) при t ϵ [α,β] является отрезок [а; b ]; 3) φ(α) = а и φ(β) = b, то 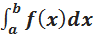=  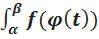* φ ’( t ) dt

Формула называется формулой замены переменной в определенном интеграле. Отметим, что:
1) при вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется
2) часто вместо подстановки х = φ(t) применяют подстановку t = g(x)
3) не следует забывать менять пределы интегрирования при замене переменных!

Интегрирование по частям при вычислении определённого интеграла.

Пусть U(x) и V(x) - дифференцируемые функции. Тогда d ( U ( x ) V ( x )) = U ( x ) dV ( x ) + V ( x ) dU ( x ) . Поэтому U ( x ) dV ( x ) = d ( U ( x ) V ( x )) – V ( x ) dU ( x ) . Вычисляя интеграл от обеих частей последнего равенства, с учетом того, что ∫ d ( U ( x ) V ( x ))= U ( x ) V ( x )+ C , получаем соотношение

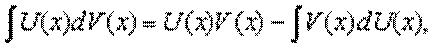
Называемое формулой интегрирования по частям. Понимают его в том смысле, что множество первообразных, стоящее в левой части, совпадает со множеством первообразных, получаемых по правой части.

Вычисление площадей плоских фигур в прямоугольных и полярных координатах

Допустим, что фигура D предполагает наличие границы ծ D : y = f ( x ), x = a , x = b ( a < b ), f ( x )ϵ C [ a , b ]
D является криволинейной трапецией и 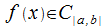, при условии, что f ( x )>0 на [ a , b ].

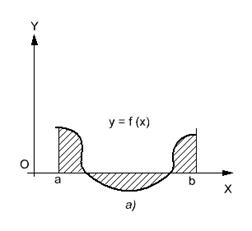
Если D находится ниже оси [ a , b ] (рис. 18.1), то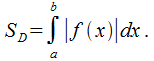

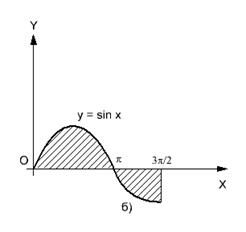
Под полярной системой координат понимается совокупность т. O (полюса) и исходящей из данной точки направленной полупрямой l (полярной оси). В качестве полярных координат т. M обозначают числа 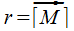(полярный радиус) и 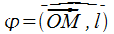(полярный угол) (рис. а).

Вычисление длины дуги плоской кривой.

Кривой линией l -наз. непрерывное отображение отрезка трехмерного пространства. Кривая наз. плоской если она целиком лежит в какой-то плоскости.

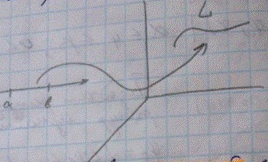
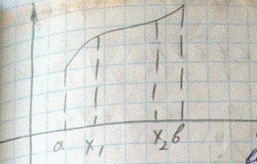
Замечание: Кривую L можно задавать в виде( параметрическое задание кривой) :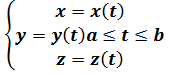
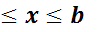На плоскости бывает задана в таком виде: или в явном виде y = f ( x ) a Предположим, что функция y = f ( x ) непрер. дифференц. Разобьем отрезок [ a , b ] на n частичных отрезков и рассм.точки на кривой с координатами. Рассмотрим ломаную соверш.в этих точках, тогда длина кривой L =