 |
Главная |
Касательная плоскость и нормаль к поверхности
|
из
5.00
|
Касательная плоскость к поверхности в её точке 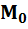 (точка касания) есть плоскость, проходящая через
(точка касания) есть плоскость, проходящая через 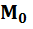 и содержащая в себе все касательные, проведённые в точке
и содержащая в себе все касательные, проведённые в точке 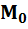 ко всевозможным кривым, проведённым на поверхности через точку
ко всевозможным кривым, проведённым на поверхности через точку 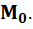
Нормалью к поверхности в точке 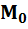 называется прямая, проходящая через точку
называется прямая, проходящая через точку 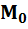 и перпендикулярная к касательной плоскости, проведённой в этой точке.
и перпендикулярная к касательной плоскости, проведённой в этой точке.
Если уравнение поверхности имеет вид F(x, y, z)=0, то уравнение касательной плоскости в точке 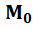 (
( 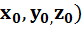 имеет вид:
имеет вид:
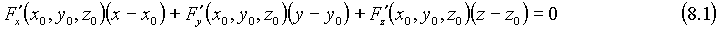
Уравнение нормали к этой поверхности в точке 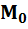 есть
есть

В случае явного задания поверхности уравнением (8.1) и (8.2) примут вид

Частные производные и дифференциалы высших порядков


Экстремумы функций нескольких переменных.

Условный экстремум
Функция u = f ( 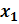 ,…,
,…, 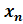 ) имеет условный максимум (минимум) в точке
) имеет условный максимум (минимум) в точке 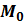 (
( 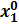 ,…,
,…, 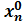 ),если существует такая окрестность точки
),если существует такая окрестность точки 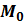 для всех точек которой, удовлетворяющих уравнениям связи
для всех точек которой, удовлетворяющих уравнениям связи 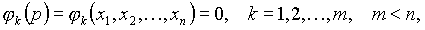 выполняется неравенство f (
выполняется неравенство f ( 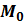 )>f(M), (f(
)>f(M), (f( 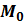 )< f ( M )).
)< f ( M )).
Исследование функции на условный экстремум сводят к исследованию на обычный экстремум функции Лагранжа 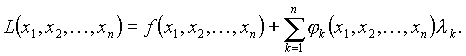 Константы
Константы 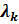 , k =1,2,…, m ) называют множителями Лагранжа. Необходимые условия условного экстремума выражаются системой
, k =1,2,…, m ) называют множителями Лагранжа. Необходимые условия условного экстремума выражаются системой  Решение системы
Решение системы 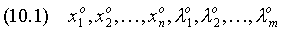 даёт координаты точки
даёт координаты точки 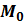 (
( 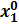 ,…,
,…, 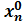 ) (или системы точек), в которой возможен условный экстремум.
) (или системы точек), в которой возможен условный экстремум.
Достаточные условия условного экстремума вытекают из исследования на знак 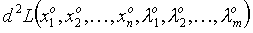 при условии, что дифференциалы
при условии, что дифференциалы 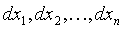 удовлетворяют уравнениям
удовлетворяют уравнениям
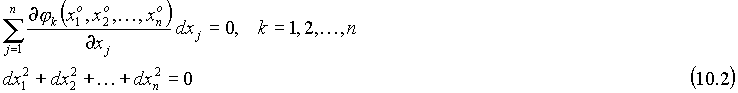
Точнее говоря, функция n u = f ( 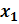 ,…,
,…, 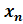 ) имеет условный максимум (минимум) в точке
) имеет условный максимум (минимум) в точке 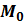 (
( 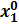 ,…,
,…, 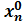 ) , если для всевозможных наборов
) , если для всевозможных наборов 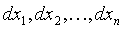 , удовлетворяющих (10.2), выполняется неравенство
, удовлетворяющих (10.2), выполняется неравенство
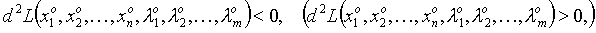
24. Обыкновенные дифференциальные уравнения (основные понятия).
При решении различных задач математики, физики, химии и других наук часто пользуются математическими моделями в виде уравнений, связывающих независимую переменную, искомую функцию и ее производные. Такие уравнения называются дифференциальными. Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество .
Так, решением уравнения у’ = f(x) является функция у = Р(х) -первообразная для функции f(x). Рассмотрим некоторые общие сведения о дифференциальных уравнениях (ДУ).
Если искомая (неизвестная) функция зависит от одной переменной, то ДУ называют обыкновенным; в противном случае - ДУ в частных производных. Далее будем рассматривать только обыкновенные ДУ.
Наивысший порядок производной, входящей в ДУ, называется порядком этого уравнения.
Например, уравнение y’’’- Зу'' + 2у = 0 - обыкновенное ДУ третьего порядка, а уравнение x^2y' + 5ху = y^2 - первого порядка; у *z_x^' = x*z_y^' - ДУ в частных производных первого порядка.
Процесс отыскания решения ДУ называется его интегрированием, а график решения ДУ – интегральной кривой.
25. Дифференциальные уравнения первого порядка. Задача Коши. Теорема существования и единственности решения задачи Коши (формулировка)
Дифференциальное уравнение первого порядка в общем случае можно записать в виде
F(x; у; у') = 0 ( 48.1)
Уравнение связывает независимую переменную х, искомую функцию у и ее производную у'. Если уравнение (48.1) можно разрешить относительно у', то его записывают в виде
у' = f(x; у) (48.2)
и называют ДУ первого порядка, разрешённой относительно производной. Мы в основном будем рассматривать эту форму записи ДУ.
Уравнение (48.2) устанавливает связь (зависимость) между координатами точки (х; у) и угловым коэффициентом у' касательной к интегральной кривой, проходящей через эту точку. Следовательно, ДУ у' = f(x; у) дает совокупность направлений (поле направлений) на плоскости Оху. Таково геометрическое истолкование ДУ первого порядка.
Кривая, во всех точках которой направление поля одинаково, называется изоклиной. Изоклинами можно пользоваться для приближенного построения интегральных кривых. Уравнение изоклины можно получить, если положить у' = с, т. е. f(x; у) = с.
Дифференциальное уравнение первого порядка, разрешенное относительно производной, можно записать в дифференциальной форме: Р(х; у) dx + Q(x; у) dy = 0, (48.3), где Р(х; у) и Q(x; у) - известные функции. Уравнение (48.3) удобно тем, что переменные х и у в нем равноправны, т. е. любую из них можно рассматривать как функцию другой. Отметим, что от одного вида записи ДУ можно перейти к другому.
Интегрирование ДУ в общем случае приводит к бесконечному множеству решений (отличающихся друг от друга постоянными величинами). Легко догадаться, что решением уравнения у' = 2х является функция у = 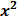 , а также у =
, а также у = 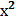 + 1, у =
+ 1, у = 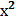 –
– 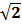 и вообще у =
и вообще у = 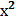 + с, где с - const.
+ с, где с - const.
Чтобы решение ДУ приобрело конкретный смысл, его надо подчинить некоторым дополнительным условиям.
Условие, что при х = 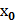 функция y должна быть равна заданному числу
функция y должна быть равна заданному числу 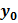 , т. е. у =
, т. е. у = 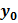 называется начальным условием. Начальное условие записывается в виде y(
называется начальным условием. Начальное условие записывается в виде y( 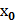 ) =
) = 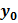 или ylx=
или ylx= 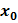 =
= 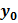 (48.4)
(48.4)
Общим решением ДУ первого порядка называется функция у = ϕ(x; с), содержащая одну произвольную постоянную и удовлетворяющая условиям:
1. Функция ϕ(Х; с) является решением ДУ при каждом фиксированном значении с.
2. Каково бы ни было начальное условие (48.4), можно найти такое значение постоянной с = 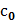 , что функция y = ϕ(х;
, что функция y = ϕ(х; 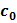 ) удовлетворяет данному начальному условию.
) удовлетворяет данному начальному условию.
Частным решением ДУ первого порядка называется любая функция y = ϕ(Х; 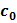 ), полученная из общего решения у = ϕ(х; с) при конкретном значении постоянной с =
), полученная из общего решения у = ϕ(х; с) при конкретном значении постоянной с = 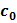 .
.
Если общее решение ДУ найдено в неявном виде, т. е. в виде уравнения Ф(х; y; с) = 0, то такое решение называется общим интегралом ДУ. Уравнение Ф(х; y; 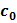 ) = 0 в этом случае называется частным интегралом уравнения.
) = 0 в этом случае называется частным интегралом уравнения.
С геометрической точки зрения y = ϕ(Х; с) есть семейство интегральных кривых на плоскости Оху; частное решение y = ϕ(х; 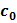 ) - одна кривая из этого семейства, проходящая через точку
) - одна кривая из этого семейства, проходящая через точку 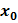 ;
; 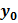 ). Задача отыскания решения ДУ первого порядка (48.3), удовлетворяющего заданному начальному условию (48.4), называется задачей Коши.
). Задача отыскания решения ДУ первого порядка (48.3), удовлетворяющего заданному начальному условию (48.4), называется задачей Коши.
Теорема1 (существования и единственности решения задачи Коши). Если в уравнении (48.2) функция f(x; y) и ее частная производная 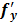 (x; y) непрерывны в некоторой области D, содержащей точку (
(x; y) непрерывны в некоторой области D, содержащей точку ( 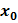 ;
; 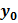 ), то существует единственное решение y = ϕ(х) этого уравнения, удовлетворяющее начальному условию (48.4)
), то существует единственное решение y = ϕ(х) этого уравнения, удовлетворяющее начальному условию (48.4)
Геометрический смысл теоремы состоит в том, что при выполнении ее условий существует единственная интегральная кривая ДУ, проходящая через точку ( 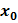 ;
; 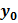 ).
).
|
из
5.00
|
Обсуждение в статье: Касательная плоскость и нормаль к поверхности |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

