Статистические модели. Этапы построения статистической модели с одной переменной

Метод статистических испытаний применяется для моделирования сложных систем, в которых не возможно или не целесообразно получить аналитические модели, описывающие протекающие процессы. Данный метод также используется в случаях, когда реальные испытания системы оказываются дорогостоящими или их не возможно проводить по причинам социального, военного и других смыслов.

Имеется объект исследования ОИ, который характеризуется набором переменных:

входных – Xj (j =1, k) и выходной – Y.

       Требуется найти зависимость выходной переменной от входных.

При этом считается, что механизмы процессов, протекающих внутри объекта исследования, неизвестны, а имеются только соответствующие значения входных и выходных параметров. Такая задача носит название задачи «черного ящика».

Рассмотрим простейший случай, когда на вход действует только одна переменная:

Решение задачи моделирования в этом случае состоит из ряда этапов:

1. проведение эксперимента;

2. выбор вида эмпирической зависимости;

3. нахождение параметров выбранной зависимости;

4. исследование модели и выводы.

На первом этапе задаем значения входной переменной X из возможного диапазона и замеряем соответствующие значения выходной переменной Y. Результат представляем в следующем виде:

По экспериментальным данным строим график:

       На втором этапе необходимо подобрать зависимость, которая могла бы описать экспериментальные данные. В таблице приведены основные типовые формулы, наиболее часто встречающиеся в задачах химии и химической технологии.

Для выбора вида зависимости воспользуемся методом средних точек. Для каждой зависимости рассчитываем координаты средних точек Xk и Yk по формулам, приведенным в таблице. Средние точки наносим на график и выбираем ту формулу, средняя точка которой лежит ближе всего к экспериментальной кривой.

На третьем этапе необходимо определить параметры выбранной зависимости a и b таким образом, чтобы расчетная кривая лежала как можно ближе к экспериментальной кривой. В качестве критерия близости выбираем минимум суммы квадратов отклонений между экспериментальными и расчетными значениями:

Условием минимума критерия Q является равенство нулю производных по параметрам a и b, что после элементарных преобразований приводит к системе нормальных уравнений для определения параметров линейной зависимости

где [X] = ∑(Xi) ; [Y] = ∑(Yi ) ; [X ²] = ∑(Xi*Xi);

[Y *X] = ∑(Yi *Xi); n – количество экспериментов.

Решив эту систему, получаем искомые значения параметров. Следует отметить, что при нахождении параметров других формул необходимо сначала привести их к линейному виду согласно таблице.

На четвертом этапе получаем расчетные значения подстановкой в найденную формулу экспериментальных значений входной величины. Полученные значения наносим на график с экспериментальными данными и делаем вывод об адекватности.

Пример:

В результате эксперимента получены следующие данные:

Находим координаты средних точек для шести зависимостей и наносим на график:

Среднее значение для формулы 4 лежит ближе всего к экспериментальной кривой, следовательно, выбираем формулу y = a + b *log( x).

В линейном виде y = a + b *z, где z = log(x).

Выбираем в качестве критерия адекватности выражение вида:

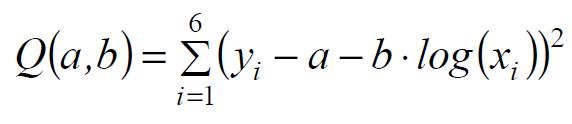
Система нормальных уравнений имеет вид:

Решив эту систему, получим искомые значения параметров а и b. Систему уравнений решим следующими способами: методом Крамера и при помощи встроенной функции lsolve (пакет Mathcad) и матричным методом.

Решение с помощью метода Крамера. Матрицу коэффициентов при неизвестных обозначим через а1, вектор правых частей системы нормальных уравнений обозначим через b1.

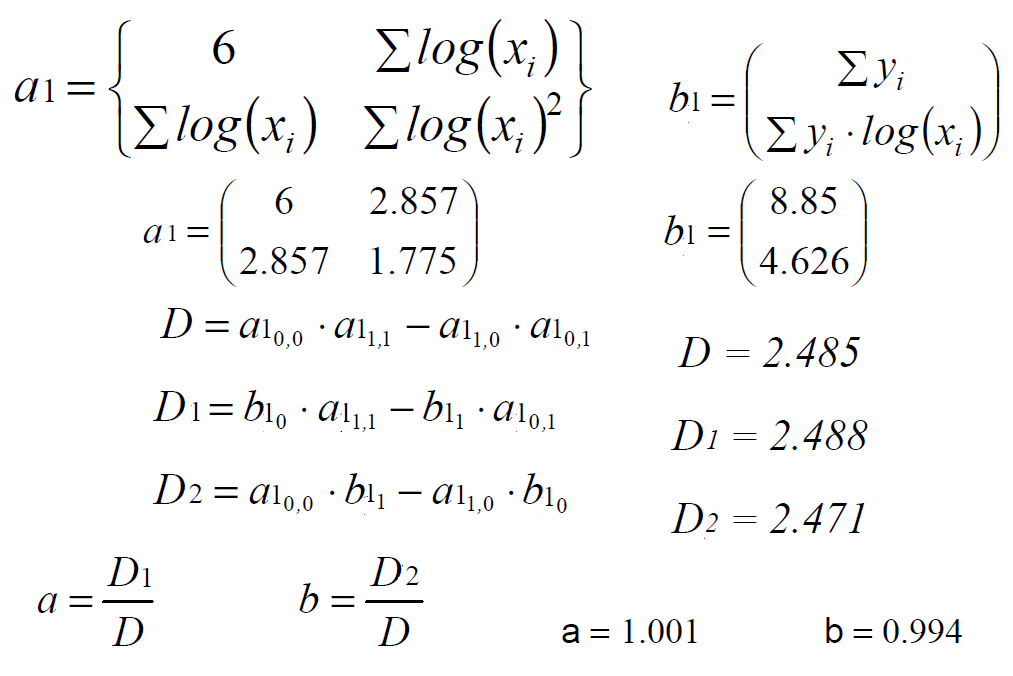
Решение при помощи функции lsolve(a1,b1):

Решение матричным методом:

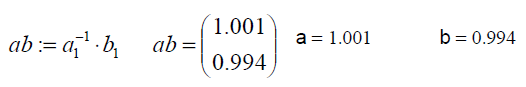
Проверка адекватности:

Выбранная формула имеет вид: Y(x) = a + b * log(x)

Экспериментальная и расчетная кривые:

Сравнение значений экспериментальной y и расчетной Y кривых, а также величина Q показывают достаточно хорошее совпадение, следовательно, исследуемый объект адекватно описывается уравнением y = 1 + log( x), значит, параметры найдены правильно.