Статистические модели. Функция многих переменных. Множественная регрессия

Общее назначение множественной регрессии (этот термин был впервые использован в работе Пирсона – Pearson, 1908) состоит в анализе связи между несколькими независимыми переменными и зависимой переменной.

Требуется найти зависимость выходной переменной от входных.

Обычно математическая модель объекта в многофакторных задачах записывается в виде полинома некоторой степени (в зависимости от требуемой точности)

где y – выходная переменная (целевая функция или параметр оптимизации); xj – входные переменные, или факторы (j=1, k); k – число факторов.

Точные значения коэффициентов уравнения определить невозможно, поэтому вместо истинных значений коэффициентов отыскиваются их оценки b. Тогда уравнениепереписывается в виде

Уравнение называется уравнением регрессии, а коэффициенты b0, bj, bjl, bjj – коэффициентами регрессии, а метод получения такого уравнения – множественной регрессией.

Первый этап решения этой задачи – выбор вида модели. В данном случае он заключается в выборе степени уравнения регрессии в зависимости от сложности решаемой задачи и требуемой точности. При первоначальном исследовании объекта обычно применяют линейное уравнение регрессии:

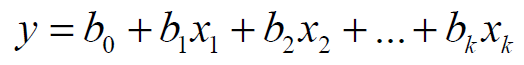
На следующем этапе выбирают уравнение второго порядка:

С тем, чтобы коэффициенты регрессии можно было определить независимо друг от друга и по более простым формулам, необходимо проводить эксперимент по заранее составленному плану.

В последнее время для моделирования и оптимизации различных процессов широко применяются методы активного планирования эксперимента. С их помощью исследователь проводит эксперимент по заранее составленному плану при минимальных затратах на получение необходимых данных об изучаемом объекте и его оптимизацию.

В большинстве случаев применяют полный факторный эксперимент (ПФЭ), в ходе которого каждый фактор варьируется на определенном числе уровней. Для линейного планирования достаточно того, чтобы каждый фактор варьировался на двух уровнях, т.е. принимал в ходе эксперимента два различных значения. Факторам присваиваются некоторые условные значения: на верхнем уровне (+1), на нижнем – (–1), которые можно получить из реальных переменных xj выбором начального значения каждого фактора xjн и интервала его варьирования Δ xj .

В общем случае число опытов ПФЭ N = 2^к

На примере двух факторов рассмотрим, как составляется таблица ПФЭ, называемая матрицей планирования.

Матрица планирования полного факторного эксперимента N = 2²

 Геометрическая интерпретация полного факторного эксперимента.

Расчет коэффициентов регрессии – третий этап моделирования осуществляем по формуле:

Причем b0 находим как среднее арифметическое всех yi (i=1,N). Полученные коэффициенты регрессии необходимо проверить на значимость, т.е. оценить величину влияния каждого фактора на значение функции цели.

Если эта величина соизмерима с ошибкой эксперимента, то соответствующий коэффициент не несет дополнительной информации об объекте и его можно приравнять нулю, что упрощает полученную модель.

Значимость коэффициентов проверяется с помощью t-критерия Стьюдента. Для этого с целью нахождения ошибки эксперимента – дисперсии воспроизводимости Sy² – проводим серию параллельных опытов в какой-либо точке, например, в центре планирования (точке, соответствующей начальным значениям факторов xjн).

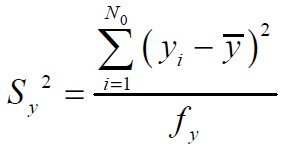
где N0 – число параллельных опытов;    – среднее значение параллельных опытов ( ); fy - число степеней свободы – величина, показывающая, какое число связей независимых наблюдений осталось не задействовано (fy = N0 – 1, т.к. одна связь использована при нахождении y ). Затем определяем значения t-критерия для каждого фактора.

Полученные значения сравниваем с табличным значением критерия Стьюдента tтабл, найденным при числе степеней свободы fy и определенном уровне значимости q – величине, характеризующей вероятность того, что решение будет неправильным (обычно q = 0,05). Если tj > tтабл, то коэффициент значимо отличается от нуля, если же tj < tтабл, то bj= 0.

Проверку адекватности уравнения регрессии (четвертый этап моделирования) проводим по F-критерию Фишера. Суть этой проверки сводится к сравнению двух дисперсий: дисперсии адекватности Sад ² и дисперсии воспроизводимости Sy ².

Если первая величина соизмерима со второй, то можно считать, что уравнение регрессии адекватно описывает экспериментальные данные; в противном случае оно неадекватно – тогда необходимо либо уменьшить интервал варьирования xj, либо увеличить порядок уравнения регрессии.

Для вычисления критерия Фишера находим дисперсию адекватности Sад ²

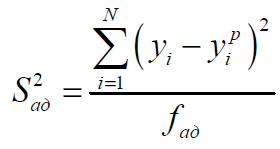
где yi ^p– расчетные значения, получаемые по уравнению регрессии; fад = N – d – число степеней свободы; d – число значимых коэффициентов.

Затем определяем расчетное значение F-критерия,

которое сравниваем с табличным значением Fтабл, найденным при степенях свободы fад и fy и уровне значимости q. Если F < Fтабл, то уравнение адекватно, если F > Fтабл – уравнение неадекватно.