Числовые множества на оси:

· Отрезок [a, b] =

· Интервал (a,b) =

· Полуотрезок [a,b) = {x принадл. R: a≤x<b}

                   (a,b] = {x принадл. R: a<x≤b}

· Бесконечный промежуток (-∞; b) = {x принадл. R: x<b ∩ -∞}

Операции над множествами:
1. Объединение (сумма):

Объединением множеств называется множества, состоящие из элементов, принадлежащих хотя бы к одному из данных множеств.

2. Произведение (пересечение):

Произведением множеств называют множество, состоящее из элементов одновременно принадлежащих всем слагаемым множествам.

3. Разность:

Разностью 2-уъ множеств называется множество, которое состоят из тех элементов уменьшаемого множества, которые не совпадают с элементами вычитаемого множества.

Определение функции. Свойства функции:

f

Функция – правило, по которому каждому элементу из одного множества ставится в соответствие единственный элемент из другого множества.

х принадл. Х           y принадл. Y

Свойства функции:

Четность и нечетность.

Функция y = f(x) четная, если выполняется f(-x) = f(x), и нечетная, если f(-x) = -f(x). В противном случае функция имеет общий вид. *(четные функции симметричны относительно оси OY)

Монотонность.

Если функция y = f(x) в точке x₂ > чем x₁ принимает значение f(x₂) > f(x₁), то она является возрастающей. Если большему значению аргумента x₂ > x₁ соответствует меньшее значение функции, то она является убывающей. Убывающие и возрастающие функции являются монотонными.

Ограниченность.

Функция y = f(x) называется ограниченной на промежутке x, если существует M > 0 для которого |f(x)| ≤ M   

Периодичность.

Функция y = f(x)является периодичной на промежутке х, если сущ. Т≠0 для которого f(x+T) = f(x)

Вопрос №29

Конечный предел функции в точке и при x →∞

Конечный предел в точке х₀:

Число А называется пределом функции y = f(x) при x→х­_0­, если для любого Е > 0 существует б > 0 такое, что при х ≠x₀, удовлетворяющее неравенству |х – х₀| < б, выполняется условие |f(x) - A| < Е

 

Предел обозначается:  = A

 

Конечный предел в точке +∞:

Число А называется пределом функции y = f(x) при x→ ₊ ∞, если для любого Е > 0 существует С > 0, такое что при x > C выполняется неравенство |f(x) - A| < Е

 

Предел обозначается: 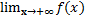 = A

 

Конечный предел в точке -∞:

Число А называется пределом функции y = f(x) при x →-∞, если для любого Е < 0 существует С < 0 такое, что при х < -С выполняется неравенство |f(x) - A| < Е

 

Предел обозначается: 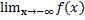 = A

 

Вопрос №30

Понятие окрестности. Общее определение конечного предела.

Понятие окрестности:

При б > 0 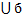(х₀) = (х₀ – б; х₀ + б) называется дельта-окрестность (б – окрестность)

 

(-∞; С) – окрестность в точке -∞

(С; +∞) – окрестность в точке +∞

 

Общее определение конечного предела:

Число А называется пределом функции y = f(x) при x→x₀, если для любого Е > 0 существует б > 0 такое, что х принадл. 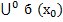 тогда f(x) принадл.  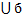(А)

 

Вопрос №31