Односторонний предел. Теорема о связи односторонних и двусторонних пределов.

Односторонний предел:

1. Если x→х₀ и при х < х₀ то говорят, что х → х₀^-

Если x→х₀ и при х >х₀ то говорят, что х → х₀⁺

 

 х→х₀^- ó х→х₀ - 0 – бесконечно малая величина.

 х→х₀⁺ ó х→х₀ + 0 – бесконечно большая величина.

 

2. Если функция y = f(x) определена высотой дельта-окрестности в точке х₀ и х→х₀^-_, то 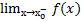 = f(x^-) – предел функции в точке х₀ слева.

 

3. Если функция y = f(x) определена высотой дельта-окрестности в точке х₀ и х→х₀⁺_, то = f(x₀⁺)

 

Теорема о связи односторонних с двусторонних пределов:

Двусторонний предел существует тогда и только тогда, когда 2 односторонних предела равны между собой.

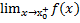 = А ó  =  = А

 

Вопрос №32

Бесконечно малая и бесконечно большая величины. Теорема о связи бесконечно малых и бесконечно больших величин.

Бесконечно малая и бесконечно большая величины:

Функция f(x) называют бесконечно малой величиной в точке х₀ принадл. R U ±∞, если

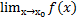 = 0

 

Функция f(x) называется бесконечно большой величиной в точке х₀ принадл. R U ±∞, если  = ∞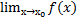

 

Теорема о связи бесконечно малых и бесконечно больших величин:

1. Пусть f(x) является бмв в точке х₀, тогда  является ббв в этой точке

2. Пусть f(x) является ббв в точке х₀, тогда  является бмв в этой точке

 

 

Вопрос №33

Свойства бесконечно малых и бесконечно больших величин.

Свойства бмв:

1. Сумма конечного числа бмв есть величина бм

2. Произведение бмв на ограниченную функцию (в том числе на постоянную, на др. бм) есть величина бм.

3. Частное  от деления бмв на функцию, предел которой ≠ 0, есть величина бм.

Свойства ббв:

1. Сумма ббв и ограниченной функции есть величина бб.

2. Произведение ббв на функцию, у которой предел ≠ 0 , есть величина бб

3. Частное от деления ббв на функцию, имеющую предел, есть величина бб.

 

Вопрос №34

Теоремы о пределах.

 

1. Предел конечной суммы функций = сумме пределов этих функций:

 = A + B

 

2. Предел произведения конечного числа функций = произведению пределов этих функций:

 = A * B     

3. Частное от деления двух функций в пределах = отношению пределов этих функций (при условии что знаменатель не является бмв)

 

 = A / B   (В≠0)!!

4. Теорема о связи предела и бмв: Для того, чтобы число А являлось пределом функции f(x) в точке х₀ необходимо и достаточно чтобы значение функции в этой точке = А + бмв

5.

f(x₀) = A + α [α] = [α(x)] - бмв

 

Вопрос №35

Первый замечательный предел  (теорема с доказательством)

 

Пусть х измеряется в радианах, тогда  = 1

Док-во:  Для выполнения доказательства проверим функцию под знаком lim на четность.

  (четная)

Т.к. функция является четной, то доказательство выполняется в I четверти, с использованием окружности единичного радиуса.

			Sin x ===  = Tg x === SΔ AOC < S сек AOC < SΔAOD SΔ AOC = * OA = sin x *1 = SΔ AOD = *OA = S сек AOC =  =
	π/2

                                                     

                                                    D

   

                                          C  

 

 

 

X

             0         x         B   A  

 

                             OA = 1

 

 

До множим все три части двойного неравенства на 2:

 Sin x < x <

Поделим все 3 части на sin x: и поскольку sin x в I четверти «+», то знаки двойного неравенства сохранятся

1<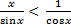

 

1<

Выполним предельный переход в точу 0:

 

1 <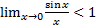

 

Т.к. нет такой величины, которая одновременно была бы и больше и меньше 1, то естественно, что первый замечательный lim =1

 

Ч.т.д.

 

Вопрос №36

Второй замечательный предел ⁿ .Следствие из второго замечательного предела.

2-ой замечательный предел ⁿ  = e

 N=1 (1+ )¹ = 2

 

N=2 (1+ )² = 2, 25

 

N=3 (1+ )³ = 2, 35

 

n→∞ e = 2,71826…

 

Следствие из второго замечательного предела:

 

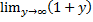^1/y  = e

х = 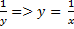                      y→0         x→∞

 

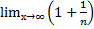ⁿ  = e – второй замечательный предел.

 

Вопрос №37