 |
Главная |
Корзина разнообразных задач
|
из
5.00
|
Введение
Полезность, важность и необходимость рекурсии, как одного из концептуальных методов решения практических задач подчеркивалась многими мэтрами информатики. Сошлемся лишь на двух лауреатов премии Тьюринга: американского специалиста по системному программированию Д.Кнута и английского теоретика информатики Ч.Хоара.
Д.Кнут широко использовал рекурсию при изложении материала в ставшем уже классическим его трехтомном выпуске “Искусство программирования для ЭВМ” [1-3]. Кроме того, он предполагал продолжить издание книг этой серии и в четвертом томе одну из двух глав назвать “Рекурсия”, полностью посвятив её рекурсивным методам решения задач [1, стр.11]. К великому сожалению, тома с 4 по 7 до сих пор не вышли. Однако в настоящее время появилась надежда, что в ближайшие годы (1999г.-2004г.) они будут дописаны и опубликованы [9].
Ч.Хоару принадлежат следующие слова “Следует отдать должное гению разработчиков Алгола-60 за то, что они включили в свой язык рекурсию и дали мне тем самым возможность весьма элегантно описать мое изобретение (речь идет о так называемой быстрой сортировке – Quick Sort). Сделать возможным изящное выражение хороших мыслей – я считал это наивысшей целью проекта языка программирования” [4, стр. 176]. К этому лишь следует добавить, что, на сегодняшний день, практически все действующие языки программирования поддерживают рекурсию.
В данном пособии дается неформальное понятие рекурсии, рассказывается об общей схеме решения задач с помощью рекурсии и приведены рекурсивные алгоритмы решения весьма разнообразных по содержанию и степени сложности задач.
Что такое рекурсия?
Понятие рекурсии достаточно просто для понимания и не связано со знанием какого-либо определенного формализма или специальной нотации. В общем случае на рекурсию следует смотреть как на введение в определение объекта ссылку на сам объект или, более определенно, как на прием сведения решения некоторой задачи к решению “более простой” задачи такого же класса. В программировании это выражается в построении программ (процедур и функций), которые при выполнении обращаются сами к себе непосредственно или через цепочку других программ. Кажущаяся при этих самовызовах или последовательных циклических вызовах видимость порочного круга (circulus vitiosus – лат.) не более чем иллюзия. Во многих конкретных случаях простыми рассуждениями путем отслеживания значений одной или нескольких управляющих величин удается провести доказательство завершимости вычислений за конечное число шагов.
Функция называется рекурсивной, если в её определении содержится вызов этой же функции. Различают простую рекурсию, когда текст программы функции F напрямую содержит вызов F, и косвенную рекурсию, когда F обращается к иным функциям, которые содержат вызов F. Поэтому, по тексту программы рекурсивность не всегда явно определима. Знание механизмов реализации рекурсии помогает эффективно её использовать. Что происходит, когда функция F выполняет рекурсивный вызов? Прежде всего, запоминается текущее состояние программы, необходимое для продолжения вычислений, когда управление снова вернется к ней. Затем F с новыми значениями аргументов начинает выполняться заново как бы с новым экземпляром программы. При следующем рекурсивном вызове F всё повторяется и т.д. до тех пор, пока очередной вызов F не приводит к какому-либо тривиальному случаю, разрешаемому без рекурсивных вызовов. Далее, в порядке, обратном тому, в котором запоминалась серия вызовов, производятся возвраты управления. В практических приложениях важно убедиться, что максимальная глубина рекурсивных вызовов не только конечна, но и достаточно мала. В противном случае не избежать переполнения стека – специально организованного участка памяти, где запоминаются отдельные состояния программы-функции.
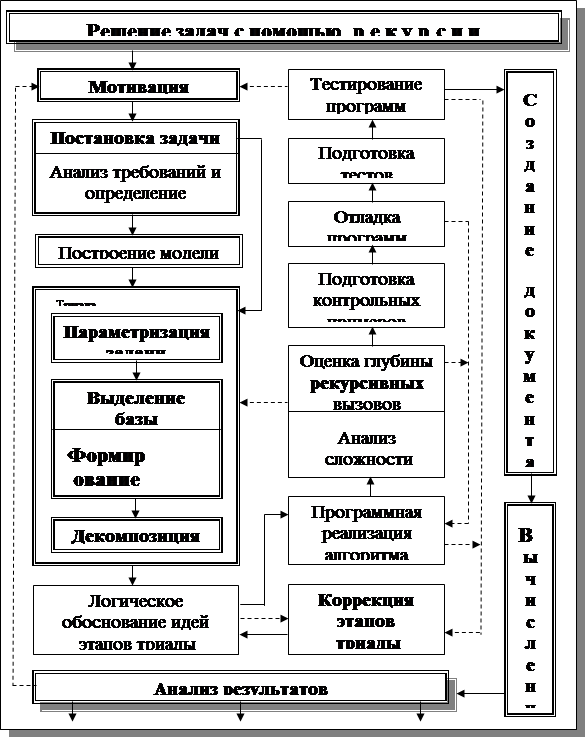
В таблице 1.1 приведена общая схема решения задач с помощью рекурсии. Эта схема обращается сама к себе и поэтому, является примером рекурсивного объекта. Решение конкретной задачи рекурсивным методом распадается на несколько шагов, основными из которых являются четыре этапа: параметризация, выделение базы и возможных правил её модификации, декомпозиция и проведение отложенных вычислений. Первые три из них называют рекурсивной триадой. В таблице 1.1 триада выделена общей рамкой. Остановимся на указанных этапах подробнее.
Параметризация задачи заключается в выявлении совокупности исходных величин, определяющих постановку и решение задачи. Значения этих параметров или некоторых из них влияют на трудоемкость решения задачи. Иногда бывает полезно ввести в рассмотрение дополнительные параметры, напрямую с постановкой задачи не связанные, но помогающие организовать рекурсию.
Выделение базы – поиск одной или нескольких подзадач, которые могут быть решены непосредственно без рекурсивного вызова.
Таблица 1.1. Рекурсивная схема решения задач с помощью рекурсии
 |
Если база будет меняться в процессе вычислений, то должен быть указан алгоритм её изменения. Как правило, подобная динамическая база расширяется за счет получения решений промежуточных задач и облегчает выполнение процесса отложенных вычислений. Возможно и сужение рекурсивной базы.
Декомпозиция общего случая есть процесс последовательного разложения исходной задачи на серию более простых подзадач, аналогичных исходной задаче, каждая из которых обычно по тому или иному признаку более близка к тривиальному случаю, чем предыдущая. Декомпозиция предполагает наличие некоторых вычислений, предшествующих и способствующих переходам к более простым подзадачам. Их удобно называть предварительными вычислениями. Декомпозицию необходимо осуществлять так, чтобы несложно было доказать, что при любом допустимом наборе значений параметров, рано, или поздно, она приведет нас к одному из выделенных тривиальных случаев, то есть к базе.
Проведение отложенных вычислений. На последнем этапе, решая одну за другой полученные на этапе декомпозиции подзадачи в порядке обратном их получению, мы добираемся до решения исходной задачи. Этот этап непосредственно опирается на соответствующие предварительные вычисления (предвычисления).
Нелишне заметить, что некоторые преподаватели информатики в школах и вузах имеют стойкое предубеждение против рекурсии, неправомерно преувеличивают затраты ‘памяти-времени’ в рекурсивных алгоритмах и считают эти затраты весьма расточительными. Исходя из этой предпосылки, они и действуют, пропагандируя использование итерации даже в тех случаях, когда имеют дело по существу с рекурсивными алгоритмами или с данными, имеющими рекурсивную природу. Причины недостаточного внимания к рекурсии в текущем нормативном преподавании можно разделить на следующие.
Исторические. Устоявшиеся традиции преподавания математики и информатики и нерекурсивность начальных версий первых языков программирования высокого уровня Кобола и Фортрана. Тем не менее, стоит отметить, что многие известные авторы, ориентируясь в своих книгах, статьях и учебных пособиях тридцати-сорокалетней давности на Фортран, весьма широко использовали рекурсию в практике вычислений. При этом, нерекурсивность языка в каждом конкретном случае написания рекурсивного алгоритма требовала от них большой выдумки и изобретательности.
Психологические. Отсутствие диспозиционной и ситуационной мотиваций (побудительных причин) у большинства преподавателей и их неподготовленность как в школе, так и в вузе, к рекурсивным рассуждениям.
Педагогические. Консерватизм образовательной среды по отношению к содержанию предметной области;
Методические. Отсутствие устоявшейся рабочей терминологии и понятийного аппарата, а также полноценных и доступных методических разработок по рекурсивным методам решения задач.
Технические. Недостаточные ресурсы быстродействия и, в особенности, оперативной и дисковой памяти учебных компьютеров в недавнем прошлом, а зачастую и в настоящее время.
Технологические. Отсутствие средств отладки во многих языках программирования и полное отсутствие специализированных средств отладки и тестирования рекурсивных процедур и функций.
О терминологии
В предыдущем пункте, поясняя, что такое рекурсия, мы были вынуждены ввести в рассмотрение несколько специальных терминов. Этот ряд необходимо продолжить. К минимальному набору, требующих прочного усвоения студентами, понятий и терминов следуют отнести следующие смысловые единицы: рекурсия, рекурсивный алгоритм, прямая рекурсия, косвенная рекурсия, рекурсивные обращения, рекуррентные соотношения (возвратные последовательности), производящая функция, параметризация задачи, вспомогательные параметры рекурсии, рекурсивная база, индикаторы завершения рекурсивных вызовов, пространство параметров, полная рекурсивная траектория, рекурсивная траектория, глубина рекурсивных вызовов, декомпозиция, предварительные вычисления, отложенные вычисления, повторительная рекурсия, рекурсивная триада, рекурсивные вычисления, прямой и обратный ход рекурсии, рекурсивный стек, динамическая рекурсивная база, срез рекурсивных вычислений, формуляр, воплощение, рекурсограмма, рекурсивная машина обработки формуляров, рекурсивная тавтология, адаптивный рекурсивный алгоритм, визуальное мышление, рекурсивное мышление. С учетом пояснений некоторых из этих терминов, сделанных в предыдущем пункте, смысл большей части остальных терминов становиться интуитивно ясным. Тем не менее, дадим им короткие пояснения (неформальные определения). Это позволит в дальнейшем избегать неточностей или двусмысленностей при описании рекурсивных алгоритмов. Все эти краткие неформальные определения собраны в таблицу 2.1
Таблица 2.1. Понятия и термины, связанные с рекурсией
| № | Понятие, Термин | Неформальное определение, пояснение |
| 1. | Рекурсия | 1. Введение в определение объекта ссылку на сам объект. 2. Прием сведения решения некоторой задачи к решению серии задач, подобных исходной. 3. Свойство алгоритмической системы на промежуточных этапах своего функционирования создавать другие системы, включая идентичные себе самой, и использовать результаты их функционирования в дальнейшей работе. При достаточно широкой трактовке понятия алгоритмической системы концепция рекурсивности отражает основные формы развития материи и является одним из важнейших методов познания. |
| 2. | Рекурсивный алгоритм (процедура, функция) | 1. Алгоритм (функция, процедура) называется рекурсивным, если в его определении содержится прямой или косвенный вызов этого же алгоритма. 2. Рекурсивная функция - одно из математических уточнений интуитивного понятия вычислимой функции. |
| 3. | Прямая рекурсия | Непосредственный вызов алгоритма (функции, процедуры) F из текста самого алгоритма F. |
| 4. | Косвенная рекурсия | Циклическая последовательность вызовов нескольких алгоритмов (функций, процедур) F1, F2, … Fk друг друга: F1 вызывает F2, F2 вызывает F3, …, Fk вызывает F1 (k>1). |
| 5. | Рекурсивные обращения (рекурсивные вызовы) | Прямая или косвенная рекурсия при рекурсивных вычислениях |
| 6. | Рекуррентное соотношение (рекуррентная формула) | Формула вида an+p=F(an, an+1,…, an+p-1) (p³1), позволяющая вычислять любой член бесконечной последовательности a1, a2,…, если заданы её первые p членов. Определяемая рекуррентной формулой последовательность называется возвратной. |
| 7. | Производящая функция | Производящей функцией числовой бесконечной последовательности a1, a2,…, называют степенной ряд вида: 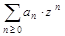 , с вещественной или комплексной переменной z. , с вещественной или комплексной переменной z.
|
| 8. | Параметризация задачи | Выявление совокупности исходных величин, определяющих постановку и решение задачи. Значения этих параметров или некоторых из них влияют на трудоемкость решения задачи. |
| 9. | Вспомогательные параметры рекурсии | Параметры, напрямую с постановкой задачи не связанные, но помогающие изменить тип рекурсии или перейти к обобщенной задаче, где рекурсия проглядывается явно. |
| 10. | Рекурсивная база | Совокупность наборов значений параметров и соответствующих им решений задачи (или простых правил для получения этих решений). Выделение базы - один из основных этапов решения задачи с помощью рекурсии. |
| 11. | Индикаторы завершения рекурсивных вызовов | Элементы постоянной или динамической рекурсивной базы. |
| 12. | Пространство параметров | Пусть tk (k=1..n) параметры задачи (алгоритма, процедуры, функции), принимающие значения из некоторых множеств объектов Mk (k=1..n). Декартово произведение M множеств Mk (k=1..n) называется пространством параметров задачи. Таким образом, элементами M являются наборы (упорядоченные множества) объектов m1, m2, … mn, где mkÎMk (k=1..n) вида: (m1, m2, … mn). Областью определения параметризованной задачи, является совокупность элементов пространства параметров, при которых она имеет решение. |
| 13. | Полная рекурсивная траектория | Пусть F(X), где X=(x1, x2, … xn) - рекурсивная функция, которую требуется вычислить в некоторой точке X0. Конечная последовательность аргументов F(X) вида: X0, X1, …Xn называется рекурсивной траекторией, если элементы Xk (k =1..n) - суть наборы параметров при последовательных рекурсивных вызовах, а Xn принадлежит базе рекурсии. |
| 14. | Рекурсивная траектория | Любая начальная подпоследовательность полной рекурсивной траектории. |
| 15. | Глубина рекурсивных вызовов | Количество элементов полной рекурсивной траектории в пространстве параметров. |
| 16. | Декомпозиция Предварительные вычисления (предвычисления) | Процесс последовательного разложения задачи на серию более простых подзадач, аналогичных исходной задаче, каждая из которых обычно по тому или иному признаку более близка к тривиальному случаю, чем предыдущая. Декомпозиция предполагает наличие некоторых вычислений, предшествующих и способствующих переходам к более простым подзадачам. Назовем их предварительными вычислениями или предвычислениями. Декомпозицию необходимо осуществлять так, чтобы несложно было доказать, что при любом допустимом наборе значений параметров, рано, или поздно, она приведет нас к одному из выделенных тривиальных случаев, то есть к задаче с набором параметров, являющемся индикатором завершения рекурсивных вызовов. |
| 17. | Отложенные вычисления Повторительная рекурсия | Вычисления, проводимые после того, как рекурсивная траектория попала в базу, то есть стала полной. Возможно, что отложенные вычисления состоят лишь из серии передач значений и управления в порядке, обратном рекурсивным вызовам. В этом случае реальные отложенные вычисления отсутствуют, а соответствующая рекурсия называется повторительной. |
| 18. | Управляющие параметры рекурсии (управляющий параметр) | Параметры задачи, с помощью которых организуется её декомпозиция, обеспечивающая правила выполнения рекурсивных вызовов, а также предварительных и отложенных вычислений. |
| 19. | Рекурсивная триада | Три основных этапа решения задач с помощью рекурсии: параметризация, выделение базы (или выделение начальной базы и правил её изменения), декомпозиция. |
| 20. | Рекурсивные вычисления Прямой и обратный ход вычислений | Вычисления, проводимые с помощью рекурсивных алгоритмов. Они состоят из двух стадий, называемых прямым ходом и обратным ходом. Первая из них соответствует совокупности всех предвычислений, реализуемых до входа рекурсивной траектории в базу, а вторая - совокупности отложенных вычислений, производимым после встречи с индикатором завершения рекурсивных вызовов. |
| 21. | Рекурсивный стек | Область памяти, в которую заносятся значения всех локальных переменных алгоритма (программы) в момент рекурсивного обращения. Каждое такое обращение формирует один слой данных стека. При завершении вычислений по конкретному обращению a из стека считывается соответствующий ему слой данных, и локальные переменные восстанавливаются, снова принимая значения, которые они имели в момент обращения a. |
| 22. | Динамическая рекурсивная база | Рекурсивная база, меняющаяся в процессе вычислений. Как правило, она расширяется за счет получения решений промежуточных задач и облегчает выполнение процесса отложенных вычислений. Возможно и сужение рекурсивной базы. |
| 23. | Срез рекурсивных вычислений | При решении задачи каждое рекурсивное обращение, в том числе и начальный запуск вычислений, инициируют работу как бы со ‘своим экземпляром’ исходного алгоритма. Последовательность вычислений значений локальных и глобальных переменных, соответствующая одному конкретному ‘виртуальному экземпляру’ алгоритма и не включающая в себя вычисления по вызовам из данного экземпляра (но использующая их результаты!), называется срезом рекурсивных вычислений. |
| 24. | Формуляр | Специально разработанный расчетный бланк, в котором фиксируется протокол вычислений конкретного рекурсивного среза. Формуляр может быть задан таблицей, деревом Канторовича или иным способом. В нем должны указываться взаимосвязь шагов вычислений и, кроме того, предлагаться место для проведения вычислений. |
| 25. | Воплощение | Заполненный формуляр. Воплощение формируется для каждого рекурсивного среза на отдельном формуляре. Это же самое касается и всех вызовов нерекурсивных подпрограмм, для которых должны быть разработаны свои собственные формуляры. |
| 26. | Рекурсограмма | Последовательность воплощений, соответствующая последовательности рекурсивных вызовов. |
| 27. | Рекурсивная машина обработки формуляров | Если правила заполнения формуляров при решении определенного круга задач с помощью рекурсии некоторым образом формализованы, то этот процесс может быть автоматизирован. В этом смысле можно говорить о виртуальной рекурсивной машине по заполнению формуляров. |
| 28. | Рекурсивная тавтология | Прямое или косвенное обращение рекурсивной функции (алгоритма) к самой себе с набором значений параметров, с которого начиналось вычисление этой функции. |
| 29. | Адаптивный рекурсивный алгоритм | Алгоритм, который благодаря рекурсивности учитывает те или иные индивидуальные характеристики решаемой задачи из области своего определения. |
| 30. | Визуальное мышление | 1. Способ решения интеллектуальных задач с опорой на внутренние визуальные образы. 2. Вид мышления, продуктом которого является порождение новых образов, создание новых визуальных форм, несущих определенную смысловую нагрузку. |
| 31. | Рекурсивное мышление | 1. Способ решения прикладных задач с преимущественной опорой на рекурсивные алгоритмы. 2. Разновидность математического (диалектического, продуктивного) мышления, позволяющая видеть рекурсию там, где она на первый взгляд не просматривается. |
Замечания. В таблице описаны термины и понятия, связанные с рекурсией и используемые в информатике. Их оказалось чуть более 30. При этом многие понятия вводятся впервые. В то же время подобных слов и словосочетаний, активно используемых в математике порядка 300.
Корзина разнообразных задач
Как для конкретной задачи построить рекурсивный алгоритм её решения? - готовых рецептов не существует. Некоторые практические рекомендации на этот счет приведены в [6, стр. 144]. Однако лишь ознакомление с достаточным количеством учебных рекурсивных алгоритмов позволит выработать определенную интуицию в выборе тактики и стратегии поиска и обнаружения спасательной рекурсии в незнакомой обстановке и заложить фундамент для освоения, совершенствования и отработки техники рекурсивного программирования. Общие рекомендации здесь могли бы быть такими. Пытаясь искать рекурсивное решение какой-либо задачи, следует опираться на одну из предлагаемых ниже именованных схем.
· Схема 1 - “увидеть”. Увидеть непосредственную рекурсию в определении объекта. Во многих задачах условия не просто задают её постановку, но делают это рекурсивно. Отсюда и рекурсивные программы, являющиеся точной копией условий задачи. Смотри задачи ??? .
· Схема 2 - “переформулировать”. Часто в условиях задачи не только не проглядывается рекурсия, но и сама задача неявляется алгоритмически сформулированной. Иногда её простая перефразировка, а чаще построение математической модели позволяют вдруг обнаружить первоначально скрытую рекурсию. Смотри задачи ???.
· Схема 3 - “обобщить (погрузить, вложить)”. Если из постановки задачи рекурсию извлечь не удаётся, то за счет перехода к её некоторому обобщению иногда это сделать можно. При этом предполагается, что из решения обобщенной задачи без особого труда может быть получено решение исходной задачи. Как правило, переход к обобщенной задаче происходит за счет введения дополнительных параметров. В некоторых случаях рассматриваемая схема может быть использована для перехода от одного типа рекурсии к другому. Смотри задачи ???.
· Схема 4 - “найти родственника”. Иногда к исходной задаче удается найти одну или несколько вспомогательных родственных к ней задач так, что в совокупности, взаимно дополняя друг друга, они уже будут определять вполне просматриваемую косвенную рекурсию. Смотри задачи
· Схема 5 - “обнаружить характеристическое свойство”. Пусть совокупность всех или части условий задачи оформлена в виде некоторого предиката над наборами входных данных и возможных результатов. Такой предикат определяет некоторое характеристическое свойство задачи. Формальная запись предиката с одной стороны позволяет проводить независимую “экспертную” проверку правильности работы ранее разработанных алгоритмов решения данной задачи, а с другой стороны, может оказать существенную помощь для отыскания новых рекурсивных алгоритмов её решения. При этом иногда целесообразно преобразовать предикат, то есть переформулировать характеристическое свойство задачи так, чтобы из него можно было извлечь какой-либо иной алгоритм. В любом случае, следует помнить, что характеристические свойства не всегда определяют исходную задачу однозначно.
· Схема 6 - “перенести часть условий в проверку”. Иногда при рассмотрении всех условий задачи рекурсия в явном виде сразу не обнаруживается, но удаление части условий приводит к новой вспомогательной задаче, рекурсивный алгоритм решения которой строится без особых затруднений. В этом случае, чтобы узнать, является ли полученный для новой задачи ответ (ответы) решением исходной задачи, необходимо проверить выполняются ли для него ранее удаленные условия или нет. Если решение задачи сводится к вычислению значения истинности некоторого предиката, непосредственно построенного из конъюнкции условий задачи на наборах входных данных, то описанная схема допускает возможность проверки выполнимости удаляемых условий как до использования рекурсивного алгоритма решения вспомогательной задачи, так и после этого. Смотри задачи ???.
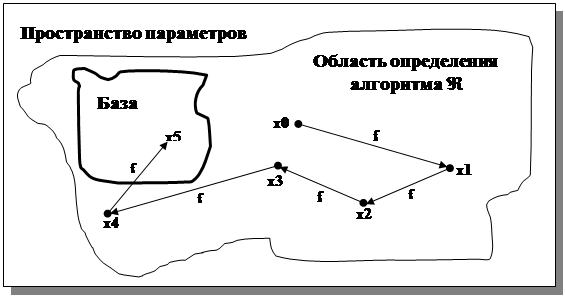
Остановимся еще на одном важном моменте. Последовательность рекурсивных обращений за конечное число шагов обязательно должна приводить нас к одному из индикаторов завершения вычислений, расположенных в базе (см. табл. 3.1, где совокупность предварительных вычислений, соответствующая прямому ходу алгоритма Â, обозначена через f). В дальнейшем остается лишь провести отложенные вычисления. Этим рекурсивные вычисления по существу отличаются от метода последовательных приближений. Однако нельзя всегда рассчитывать на окончание рекурсивного алгоритма за конечное число шагов, как на нечто само собой разумеющееся. Иногда установление этого свойства для определенного подмножества значений пространства параметров требует значительных усилий в проведении подчас непростых рассуждений.
Таблица 3.1. Схематическое изображение последовательности рекур-
сивных обращений и формирования полной рекурсивной траектории
В оставшейся части данного пункта рассматривается серия простых учебных демонстрационных задач, решения которых получаются с помощью рекурсивно определенных алгоритмов. Во многих случаях детально обсуждаются описанные выше схематические приемы поиска этих алгоритмов. В основном все программы-функции написаны на языке программирования вычислительной среды Mathcad. Часть программ написана на языке Object Pascal 5.0 системы объектного визуального программирования Delphi 5. Для некоторых задач предлагается несколько вариантов программ. Приводятся контрольные примеры. Заметим, что, ввиду разноплановости предложенных задач, многие из них могут служить отдельными темами, собирающими вокруг себя родственный содержательный материал по рекурсии для отработки техники рекурсивного программирования в рамках конкретного направления.
Результатом проработки материала данного пункта должно стать убеждение, что писать рекурсивные программы, как правило, несложно, а получаемые при этом тексты весьма компактны и, по причине отсутствия в них диких зарослей языковых украшательств, легко читаются. Нам представляется, что читатель вряд ли откажет себе в удовольствии написать собственные программы-функции решения многих из приведенных задач или их обобщений.
Факториал
Задача 1. Составить программу-функцию вычисления факториала целого неотрицательного числа n.
Решение. Для целых неотрицательных чисел n факториал n обозначается через n! и определяется так:
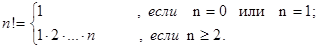
В данном случае параметризация задачи осуществлена в её постановке. Остается лишь ввести более приемлемое для нас обозначение искомой функции. Пусть это будет facto(n). Тривиальные случаи, для которых задача решается без рекурсивных вызовов, также очевидны: facto(0)=1, facto(1)=1. Они и составляют базу рекурсии. Декомпозиция по параметру n реализуется по формуле: facto(n) = n×facto(n–1) (n = 1, 2, …). Поэтому вычисления facto(n) можно организовать так:
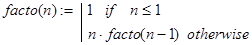
Контрольные примеры.
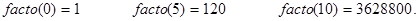
Понять процесс реализации рекурсивных вызовов, то есть декомпозицию, и возвратов управления при организации отложенных вычислений facto(n) можно из схемы рис. 3.1 (n = 3). Там около стрелок в круглых скобках жирными цифрами указаны номера последовательных шагов вычислений: (1), (2), (3) - декомпозиция; (4), (5), (6) - отложенные вычисления.
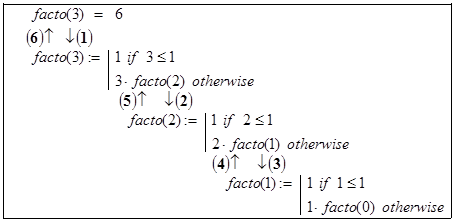
Рис. 3.1. Схематическое изображение рекурсивных вызовов и
отложенных вычислений при нахождении facto(3) = 3!.
Замечание. С помощью встроенной функции if() предложенный алгоритм удается записать еще короче. Это же касается и многих других примеров.
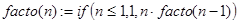
Для решения конкретной задачи иногда удается построить несколько различных рекурсивных алгоритмов. Например, функцию facto(n) можно было бы определить и так.
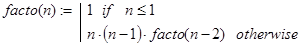
По сравнению с прежней реализацией facto() здесь количество рекурсивных вызовов уменьшается практически в 2 раза. В реальных ситуациях подобный фактор может оказаться решающим при выборе того или иного алгоритма.
Используем теперь для вычисления n! cформулированную выше схему 3 (обобщить). Если вместо исходной функции facto(n)=n!, ввести в рассмотрение функцию двух переменных fa(n, l)=l×n! (n=0,1,…), то получим равенства:
fa(n, l)=l×n×(n-1)×…×1=(l×n)×(n-1)!=fa(l×n)×(n-1)!,
fa(1, l)=l , fa(n,1)=n!.
Первое из этих соотношений может служить правилом декомпозиции, второе - определять рекурсивную базу, а третье - показывает, как вычислять n!. Соответствующая рекурсивная программа-функция могла бы выглядеть так:
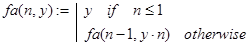
В чем же отличие этой функции от первого варианта функции facto(n)? Дело в том, в facto(n) формирование n! реализуется при проведении отложенных вычислений, в то же время нахождение fa(n, l) проводится вообще без отложенных вычислений. Особенно наглядно это видно на рисунках 3.1 и 3.2. На шагах 4, 5 и 6, отмеченных на рис. 3.2 жирными цифрами в круглых скобках, происходит лишь передача значений. Иными словами здесь мы имеем повторительную рекурсию.
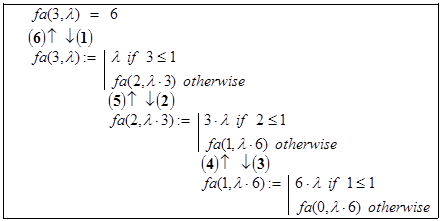
Рис. 3.2. Схематическое изображение рекурсивных вызовов
при нахождении fa(3,l) = l×3!.
Еще один вариант вычисления n! можно реализовать с помощью рассмотренной ниже в задаче 20 функции Кадью.
Сложный процент
Задача 2. Вкладчик положил в сбербанк сумму в sum единиц под p процентов за один период времени (год, месяц, неделя и т.д.). Составить программу-функцию возвращающую величину вклада по истечении n периодов времени (n = 1, 2,).
Решение. Пусть invest(sum,p,n) искомая функция. Для данной задачи вычисления значений invest() можно проводить по формуле
invest(sum,p,n) = sum×(1+p/100)n .
Однако, в учебных целях, нас интересует рекурсивный вариант алгоритма решения задачи. Рекурсию будем осуществлять по параметру n. Тривиальный случай очевиден. Если вклад положен на хранение и взят сразу, то есть до истечения первого периода времени начисления процентов, то возврату подлежит начальная сумма вклада - sum. Далее, декомпозиция может быть реализована исходя из следующего факта. Положить некоторую сумму в банк на n периодов – это то же самое, что положить эту сумму на n – 1 периодов и затем полученную сумму положить на 1 период. Соответствующий вариант программы-функции решения задачи выглядит так:
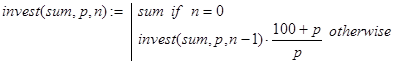
Контрольные примеры.

Схема рекурсивных вызовов здесь такая же, как при вычислении значений функции facto(n). Нетрудно видеть, что общее количество рекурсивных вызовов при вычислении invest(sum,p,n) равно n. При необходимости можно было бы уменьшить это значение до log2(n).
Степень числа
Задача 3. Пусть a - вещественное число отличное от нуля и n - целое неотрицательное число. Составить программу-функцию возвращающую величину an.
Решение. Приведенная ниже функция power(a,n) дает решение задачи за n рекурсивных вызовов:
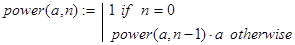
Уменьшить количество вызовов можно так. Организуем декомпозицию иначе, представив величину an в виде:
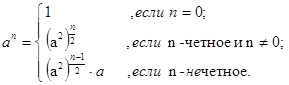
Отсюда сразу же получаем алгоритм вычисления an, требующий не более log2(n) рекурсивных вызовов. Реализуется он функцией pow(a,n):
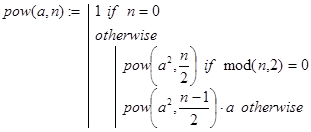
Сумма элементов массива
Задача 4. Составить программу-функцию, возвращающую сумму S компонентов вектора v=(a0,a1,…,an-1)T: S= a0+a1+…+an-1, где n³1 и ap (p=0..n-1) - вещественные или комплексные числа.
Решение. Определение суммы n слагаемых в виде:
S= a0+a1+…+an-1=(a0 +a1+…+an-2)+an-1
рекурсивно по своей сути. Сумма n слагаемых есть сумма первых (n-1)-го слагаемого плюс сумма последнего слагаемого. Этот факт и положен в основу определения функции summa(v), где v=(a0,a1,…,an-1)T.
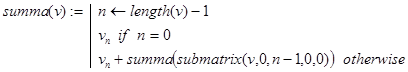
|
из
5.00
|
Обсуждение в статье: Корзина разнообразных задач |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

