 |
Главная |
Задача о Ханойских башнях
|
из
5.00
|
Рассмотрим следующую весьма популярную у студентов задачу.
Задача о Ханойских башнях. На одном из трех алмазных шпилей надето 64 круглых золотых диска. Диски имеют разные радиусы и расположены на шпиле в порядке убывания радиусов от основания к вершине. Трудолюбивые буддийские монахи день и ночь переносят диски с первого шпиля на второй, используя при необходимости и третий шпиль. При этом неукоснительно соблюдаются следующие правила.
· за один раз можно перемещать только один диск.
· больший диск нельзя располагать на меньшем.
· снятый диск необходимо надеть на какой-либо шпиль перед тем как будет снят другой диск.
Легенда утверждает, что когда монахи закончат свою работу, наступит конец света. Можно было бы подсчитать, что для решения задачи с 64 дисками потребуется 264 – 1 перемещений (около 1020). Поэтому, что касается конца света, то он произойдет по истечении пяти миллиардов веков, если считать, что один диск перемещается за одну секунду. Впрочем, и задачу и легенду для неё придумал в 1883 году математик Э. Люка. Это дает нам право отложить заботы о конце света в сторону и перейти к решению следующей задачи.
Задача 11. Составить рекурсивную программу-функцию, которая бы решала поставленную выше задачу о Ханойских башнях при количестве дисков, равном n (n = 1, 2, …).
Решение. Введем имена для шпилей: a , b , c. Пусть hanoi(n, a, b, c) искомая функция, возвращающая последовательность перемещений дисков с a на b c использованием c по вышеописанным правилам. При n = 1 решать задачу мы умеем. Необходимо просто произвести операцию “переместить a ® b”. Предположим, что мы умеем решать эту задачу для n – 1 диска. Тогда общая схема рекурсии могла бы выглядеть следующим образом.
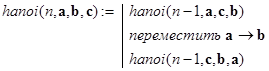
Иными словами, переместим n – 1 диск с a на с. Далее, переместим один оставшийся диск с a на b и, наконец, переместим n – 1 диск с c на b. Что нам мешает реализовать эту схему на языке программирования Mathcad? По-видимому то, что в процессе вычисления функции hanoi(n, a, b, c), мы не в состоянии организовать вывод сообщений типа “переместить a ® b”. Остается одно средство. Организовать рекурсивные обращения так, чтобы все подобные ходы-перемещения запоминались в массиве, который и будет возвращаться функцией hanoi(n, a, b, c).
Вот один из возможных вариантов определения функции hanoi():
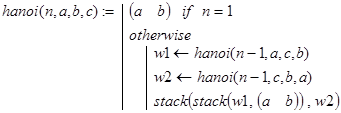
Функция возвращает матрицу размера k´2, в каждой строчке которой фиксируется перемещение одного диска (откуда, куда). Величина k равна общему количеству перемещений.
Контрольный пример. При трех дисках с именами шпилей 1, 2 и 3 получаем следующее решение:
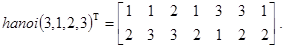
Экзотические средние
Теперь решим задачу, связанную с экзотическими средними. Рассмотрим два положительных числа а0 и b0 и составим их среднее арифметическое и среднее геометрическое. Продолжим этот процесс и, если числа an и bn уже построены, то определим an+1 и bn+1 следующим образом:
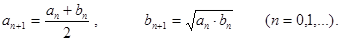 (3)
(3)
Известно, что последовательности {an} и {bn} стремятся к общему пределу и, следуя Гауссу, его называют средним арифметико-геометрическим исходных чисел а0 и b0.
Задача 12. Составить рекурсивную программу-функцию, по которой для неотрицательных чисел a и b можно было бы приближенно вычислять их арифметико-геометрическое среднее.
Решение. Параметрами задачи естественно считать исходные величины a, b и количество итераций n по формулам (3). Рекурсию организуем по n, a решением задачи будем считать матрицу (an, bn). Построить соответствующую функцию несложно и выглядеть она может, например, т
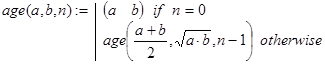
Контрольные примеры.
age(100,30,3)=[59.77675556213139 59.77665550389991],
age(100,30,5)=[59.77670553300519 59.77670553300519].
Снова отправляясь от двух положительных чисел а0 и b0 станем последовательно составлять средние арифметические и средние гармонические:
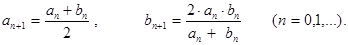 (4)
(4)
Известно, что последовательности {an} и {bn}, строящиеся по рекуррентным формулам (4), стремятся к общему пределу. Его называют средним арифметико-гармоническим исходных чисел а0 и b0. Оказывается, что среднее арифметико-гармоническое двух чисел совпадает с их средним геометрическим.
Задача 13. Составить рекурсивную программу-функцию, по которой для неотрицательных чисел a и b можно было бы приближенно вычислять их арифметико-гармоническое среднее, то есть приближенное значение 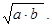
Решение. Как и в предыдущем случае, параметрами задачи естественно считать исходные величины a, b и количество итераций n по формулам (4). Рекурсию организуем по n, a решением задачи будем считать матрицу (an, bn). Соответствующая функция может выглядеть так:
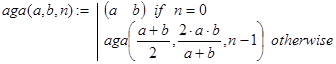
Контрольный пример.
aga(100,20,7)=[44.7213595499958 44.7213595499958],
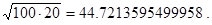
|
из
5.00
|
Обсуждение в статье: Задача о Ханойских башнях |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

