 |
Главная |
Максимальный и минимальный элементы
|
из
5.00
|
Пусть одномерный массив задан вектором 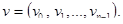 Часто возникает задача поиска максимального (минимального) элемента v. Вне зависимости от того, идет ли речь о нахождении максимального по значению элемента или его позиции в v, поиск можно реализовать за один просмотр массива. Правда в последнем случае решение может оказаться неоднозначными и постановка задачи требует уточнения. Например, отыскивается позиция максимального элемента с наименьшим индексом. В любом случае сравнение характеристик различных алгоритмов поиска проводят по количеству тех или иных выполняемых ими операций. Чаще всего это операции сравнения.
Часто возникает задача поиска максимального (минимального) элемента v. Вне зависимости от того, идет ли речь о нахождении максимального по значению элемента или его позиции в v, поиск можно реализовать за один просмотр массива. Правда в последнем случае решение может оказаться неоднозначными и постановка задачи требует уточнения. Например, отыскивается позиция максимального элемента с наименьшим индексом. В любом случае сравнение характеристик различных алгоритмов поиска проводят по количеству тех или иных выполняемых ими операций. Чаще всего это операции сравнения.
Рекурсивная функция maxv(v) находит максимальный элемент v ровно за n-1 операцию сравнения. Декомпозиция реализуется по длине вектора и опирается на такое утверждение. Решить исходную задачу для v - это то же самое, что решить её для подвектора, получаемого из v удалением его первого компонента, сравнить полученное значение с удаленным элементом и, наконец, выбрать не меньшее из них.

Контрольные примеры.

Замечание. При подсчете количества операций сравнения элементов массива не учитываются сравнения с управляющими переменными рекурсии или цикла. Это же самое касается и других программ, приведенных ниже.
Аналогично строится и функция minv(v) - нахождения за n-1 операцию сравнения минимального по значению элемента массива. Нетрудно написать рекурсивную функцию одновременного поиска минимального и максимального значений v за 2×n-2 операции сравнения. Выглядеть она может, например, так:

Контрольные примеры.
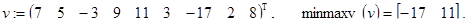
Однако одновременное нахождение максимального и минимального значений v может быть реализовано гораздо эффективней. Соответствующий результат зафиксирован в следующей задаче.
Задача 31. Написать рекурсивную программу-функцию, находящую одновременно максимальный и минимальный элементы массива v за  операций сравнения.
операций сравнения.
Решение. Если длина вектора v равна единице, то решением задачи можно считать вектор  При длине вектора v, равной двум, решение находится за одно сравнение. Пусть длина вектора больше двух. Тогда из двух первых компонентов непосредственно найдем наибольшее и наименьшее (одно сравнение), решим исходную задачу для подвектора, получающегося из v удалением этих компонентов и, наконец, осуществим правку полученного решения для подвектора за счет первых двух компонентов (два сравнения). Именно эти идеи и реализуются рекурсивной функцией minmax():
При длине вектора v, равной двум, решение находится за одно сравнение. Пусть длина вектора больше двух. Тогда из двух первых компонентов непосредственно найдем наибольшее и наименьшее (одно сравнение), решим исходную задачу для подвектора, получающегося из v удалением этих компонентов и, наконец, осуществим правку полученного решения для подвектора за счет первых двух компонентов (два сравнения). Именно эти идеи и реализуются рекурсивной функцией minmax():

Контрольный пример.
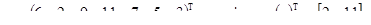
Подсчитаем теперь S - общее количество сравнений:


Тем самым решение задачи завершено полностью.
В следующем варианте minmax() - функции minmax1() используются три вспомогательных параметра: a, b, i. Первые два из них служат для фиксации текущих значений минимального и максимального элементов массива, а последний - для нумерации рекурсивных обращений. Как и в предыдущем случае, каждый рекурсивный вызов уменьшает обрабатываемый массив на два элемента. Но здесь, в отличие от minmax(), они удаляются с разных его концов. Использование вспомогательной функции mima(v) избавляет нас от сложного обращения к minmax1().


Контрольный пример.

Задача 32. Написать рекурсивную программу-функцию, находящую одновременно позиции максимального и минимального элементов массива v за 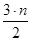 операций сравнения.
операций сравнения.
Решение. Для решения данной задачи можно использовать тот же самый алгоритм, который реализуется функцией minmax1(), подвергая запоминанию не текущие значения минимального и максимального элементов массива, а их индексы. Соответствующие функции posmima() и pmima() можно записать так:


Контрольный пример.

Замечание. Рекурсивная функция posmima() позволяет реализовать сортировку массива v по такому алгоритму:
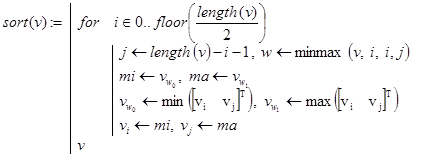
Контрольные примеры.


Абракадабра
Задача 33. Последовательность из латинских букв строится следующим образом. На нулевом шаге она пуста. На каждом последующем шаге последовательность удваивается, то есть приписывается сама к себе, и к ней слева добавляется очередная буква алфавита (a,b,c,…). По заданному числу n определить символ, который стоит на n-ом месте последовательности, получившейся после шага 26.
Решение. Эта задача предлагалась участникам областных туров Всероссийской олимпиады школьников по информатике в 1998 году. Приведем первые шаги формирования последовательности: 0 - пустая последовательность, 1 - a, 2 - baa,3 - cbaabaa, 4 - dcbaabaacbaabaa, … . Мы имеем явно рекурсивный процесс.
Построим более общую программу-функцию, чем это требуется по условиям задачи. Пусть abra(k,n) - n-ая буква в последовательности, полученной на шаге k (k=1..26). Тогда ясно, что abra(k,1) равно k-ой букве латинского алфавита. Этот факт можно взять в качестве базы рекурсии, а функцию для определения этой буквы записать так:
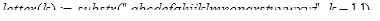
Декомпозицию удобно организовать по k, проводя “раскрутку” последовательности по шагам в обратном направлении. Это приводит к следующей функции:
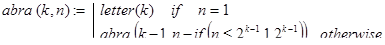
Контрольные примеры.

|
из
5.00
|
Обсуждение в статье: Максимальный и минимальный элементы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

