Вложенные многоугольники

 

Задача 34. Вложенные квадраты. Пусть на плоскости первый квадрат задан точками: M₁(-1,-1), M₂(-1,1), M₃(1,1), M₄(1,-1). Второй квадрат строится так, что вершины первого квадрата являются серединами его сторон и т.д. Составить рекурсивную программу-функцию, которая по заданному натуральному n строит систему из 2×n вложенных друг в друга описанным образом квадратов, точнее создает массив точек, последовательное соединение которых на плоскости отрезками и формирует эту систему (см. рис. 3.5).

Решение. Если учесть тот факт, что по условию задачи всегда строится четное число вложенных квадратов, то последовательность точек для построения первых двух из них можно задать непосредственно и считать соответствующую матрицу beg базой рекурсии:

 

 

Обратите внимание, что в beg каждый из квадратов задается не четырьмя, а пятью точками. При этом первая и последняя из них совпадают. Это поможет впоследствии правильной прорисовке квадратов.

Далее, декомпозиция определяется таким утверждением. Если уже построена матрица ma точек для 2×(n-1) вложенных квадратов, то, пополнив её точками матрицы , получим матрицу точек для 2×n таких квадратов. Соответствующая рекурсивная функция, базирующаяся на этих фактах, может выглядеть так:

 

 

Контрольный пример.  Результат вычислений представлен на рис. 3.5 c неодинаковым масштабом по осям.

 

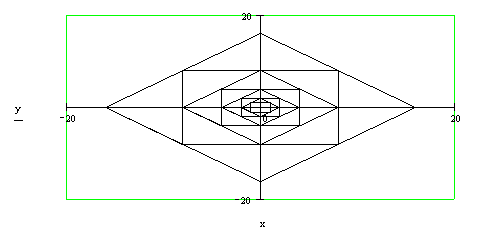
 Рис. 3.5. Вложенные 2×n квадратов (n=4)

 

Задача 35. Вложенные многоугольники. Пусть на плоскости задан правильный n-угольник, вписанный в единичную окружность одна из вершин которого имеет координаты (cos(a), sin(a)), где a - некоторый угол. Второй правильный n-угольник строится так, что его вершины являются серединами сторон первого многоугольника и т.д. Составить рекурсивную программу-функцию, которая по заданному натуральному n строит систему из n вложенных друг в друга описанным образом многоугольников, точнее создает массив точек, последовательное соединение которых на плоскости отрезками и формирует эту систему (см. рис. 3.6).

Решение. Это задача в каком-то смысле является обобщением предыдущей. Здесь выводятся правильные вписанные n-угольники, количество их не обязательно четно и первая из вершин начального n-угольника может лежать в любой точке единичной окружности. Правда, здесь многоугольники не “описываются” один вокруг другого, а “вписываются” друг в друга. Но существа дела это не меняет.

Прежде всего, составим программу, которая формирует массив вершин правильного n-угольника, вписанного в окружность радиуса r и содержащего вершину (r×cos(a) r×sin(a)). Сделать это можно, например, так:

 

 

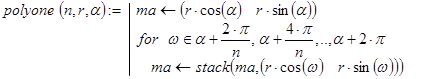
Тогда массив polyone(n,1,a) может служить базой рекурсии. Более того, эта функция при правильном выборе r и a позволяет получить массив вершин любого из следующих вписанных n-угольников, что помогает организовать и декомпозицию. Если уже построена матрица ma точек для (n-1)-го вписанного правильного n-угольника, то, пополнив её точками матрицы:

 

 

 

получим матрицу точек для 2×n таких многоугольников. Соответствующая рекурсивная функция, реализующая эти идеи, может выглядеть так:

 

 

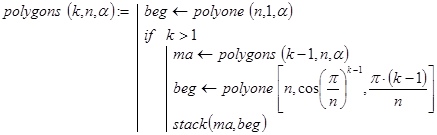
Контрольный пример. 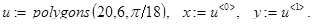 Результат вычислений представлен на рис. 3.6 c неодинаковым масштабом по осям.

 

 Рис. 3.6. k вложенных правильных n-угольников (k=20, n=6)

 

Несколько слов перед формулировкой новой задачи. В основах анализа [8, с. 17-38] операции сложения и умножения над натуральными числами определяются рекурсивным способом, опираясь на аксиомы Пеано “о существовании последующего числа” и “индукции”. Первая из названных аксиом звучит так: “для каждого натурального x имеется и притом только одно натуральное число, называемое его последующим и обозначаемое число x¢ ”. Постараемся промоделировать указанные выше и некоторые иные операции.

 
Моделирование арифметических операций

 

Задача 36. Для целых неотрицательных чисел n, m разрешены операции:

нахождения последующего числа (n+1) и предыдущего числа n-1 (n>0). Промоделировать с помощью рекурсивных функций операции нахождения суммы (n+m), разности (n-m (n³m)), умножения (n×m), возведения в степень n^m (n>0), частного и остатка при делении n на m (n/m).

Решение.

A . Сумма: a + b . Очевидноесоотношение

 

 

задает одновременно и базу рекурсии и правило декомпозиции. По нему и построена следующая рекурсивная программа-функция:

 

 

Контрольный пример:

 

B . Разность: a - b ( a ³ b ). В данном случае база рекурсии и декомпозиция могут быть извлечены из соотношения:

 

 

Соответствующая рекурсивная программа-функция выглядит так.

 

 

Контрольный пример: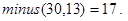

C . Умножение: a × b . Будем считать, что операция сложения уже определена. Тогда соотношение, из которого легко извлекаются база и декомпозиция для данного случая выглядит следующим образом:

 

 

Соответствующая рекурсивная программа-функция может быть записана, например, так:

 

 

Контрольный пример:

 

D . Возведение в степень: a^b ( a ¹ 0). Будем считать, что операция умножения уже определена. Тогда:

 

 

и рекурсивная программа-функция возведения в степень может быть задана так:

 

 

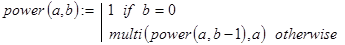
Контрольный пример: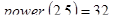  

 

E . Частное и остаток: a / b ( b >0). В данной задаче речь идет об отыскании величин q и r из представления: a=q×b+r (0£r<b, q³0). Будем предполагать, что операция вычитания уже определена, а ответ должен быть возвращен в виде вектора с двумя компонентами: (q r)^T. Если a<b, то q=0 и r=a. Этот факт и определяет базу рекурсии. Если же b>a, то a/b=1+(a-b)/b, что позволяет организовать декомпозицию. Все сказанное учтено в рекурсивной функции divi(q,a,b). В ней первый аргумент q является вспомогательным параметром. При обращениях к divi() он должен определять базовое значение частного, то есть быть равен нулю. Однако проще решать задачу с помощью вспомогательной функции div(a,b), возлагая на неё решение вопроса о правильном значении вспомогательного параметра вызовах divi(). Это довольно типичный случай при обобщениях исходной задачи за счет введения дополнительных параметров.

 

 

 

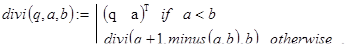
Контрольный пример.

 

Замечание. Моделирование различных операций возможно не только для целых неотрицательных чисел. Их можно было бы определить и для множества всех целых чисел и даже для множества вещественных чисел. Ограничимся рассмотрением одного примера. Напишем рекурсивную программу-функцию нахождения дробной части вещественного числа, если разрешены лишь операции x+1 и x-1. Вот один из возможных достаточно ясных вариантов её определения:

 

 

Контрольный пример.

Синтаксические языковые конструкции

 

Задача 37. Составить программу-функцию проверяющую, является ли данная последовательность символов идентификатором языка Фортран.

Решение. Будем считать, что речь идет о версиях Фортрана, где идентификатор определялся как последовательность из шести заглавных латинских букв и (или) цифр, начинающаяся с буквы и для символов была принята ASCII кодировка. Превратить последовательность символов в вектор соответствующих им ASCII-кодов можно с помощью встроенной функции str2vec(). Например:

 

 

Дополнительное ограничение на первый символ идентификатора (буква, но не цифра) усложняет общую проверку (или буква, или цифра). Чтобы действия были стандартными для всех символов, проверку первого из них будем осуществлять на допустимость отдельно в головной программе. Естественно там же располагать и проверку длины слова, которая должна находиться в пределах от 1 до 6. Тогда в подпрограмме останется решить вполне рекурсивную подзадачу: “если первый символ исходного слова не буква и не цифра, то формируем ответ “не идентификатор”. В противном случае, если длина слова равна единице, то возвращаем ответ “идентификатор”, а иначе укорачиваем слово на первый символ и снова решаем эту же подзадачу. Все сказанное и реализуется головной программой identity(word) и рекурсивной подпрограммой iden(v):

 

 

 

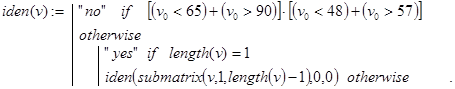
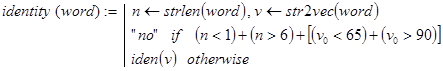
Контрольные примеры.

 

 

Замечание. В любом языке программирования все базовые языковые конструкции (идентификаторы, константы, переменные, выражения, метки, типы и т.п.) определяются рекурсивно. Особенно наглядно это видно, когда они представлены с помощью синтаксических диаграмм [7, c. 685-703] или в форме Бэкуса-Наура. Подобные определения в рамках конкретного языка программирования могут служить наборами тренировочных заданий по написанию рекурсивных программ и даже простейших рекурсивных трансляторов.

Приведем пример. Идентификатор в Паскале определяется, как и в Фортране, но без ограничений на длину последовательности символов. С помощью синтаксической диаграммы это выглядит так, как это указано на рис.3.7., а в форме Бэкуса-Наура следующим образом (значок “::=” читается как “есть по определению”):

<идентификатор>::=<буква>

<идентификатор>::=<идентификатор><буква>

<идентификатор>::=<идентификатор><цифра>

 

 

 Рис. 3.7. Синтаксическая диаграмма идентификатора (Паскаль)

И в том и в другом случаях идентификатор определяется сам через себя.

 

Проблемная ситуация

 

Задача 38. При любом ли натуральном n ли рекурсивная функция

 

равна 1?

Решение. Хотя данная строка и начата со слова “решение”, ответа на поставленный вопрос мы не знаем и, по-видимому, на сегодняшний день его не знает никто. Более того, неизвестно, для любого ли n problem(n) вычисляется за конечное число шагов. Рассмотренную задачу называют 3×n+1 проблемой. Мы включили её в список задач для того, чтобы обратить внимание читателя на следующий факт. Достаточно простые с виду рекурсивные определения функций могут таить в себе глубокие проблемы, решения которых лежат совсем не на поверхности. Тем не менее, конкретные вычисления problem(n) при разных n приводят к одному и тому же значению, равному 1. Ниже приведена рекурсивная программа для проверки истинности утверждения “problem(n)=1” при значениях n из диапазона k1..k2.

 

 

Контрольные примеры.

 

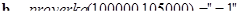
6. Задача Иосифа Флавия

 

С именем известного историка первого века Иосифа Флавия связывают следующую задачу-легенду. В ходе иудейской войны он в составе отряда из 41 воина был загнан римлянами в пещеру. Не желая сдаваться, осажденные воины решили покончить жизнь самоубийством и разработали для этого следующую процедуру. Они выстроились в круг и, начиная отсчет с конкретной позиции, каждый третий должен был убивать себя, пока не останется ни одного человека. Математически одаренный Иосиф считал подобный конец бессмысленным и потому поставил себя и своего друга на такие позиции, что после серии из 39 самоубийств они остались вдвоем, чем и спасли себе жизнь. Что это были за позиции?

Дадим этой задаче-легенде более точную и обобщенную формулировку, освободившись от суицида. При этом будем искать рекурсивные решения двух ниже приведенных задач, различающихся завершением соответствующей процедуры. Подробнее рекурсия как метод решения практических задач обсуждается в следующем параграфе.

 

Задача 1. По окружности в направлении движения часовой стрелки расположены n последовательных натуральных чисел от 1 до n. При перемещении по числам 1, 2, ... каждое k-ое число (k>1) вычеркивается (удаляется). Этот процесс продолжается до тех пор, пока чисел не станет меньше k. Определить оставшиеся числа.

 

Задача 2. По окружности в направлении движения часовой стрелки расположены n последовательных натуральных чисел от 1 до n. При перемещении по числам 1, 2, ... каждое k-ое число (k>1) вычеркивается (удаляется). Этот процесс продолжается до тех пор, пока не останется одно число. Определить его.

A . Решение первой задачи Флавия при k =2.

 

Ниже рассмотрены три варианта A1-A3 решения задачи 1 при k=2, опирающиеся на разные идеи.

A1. Если n=2×s, то после первого прохода по кругу останутся числа: 1, 3, ... 2×s-1 и следующий проход начнется с вычеркивания числа 3. Это все равно, как если бы мы начинали с s последовательных натуральных чисел от 1 до s, но каждое уцелевшее число удваивали и результат уменьшали на 1. Отсюда, если fla1(n) - функция, решающая поставленную задачу, то fla1(1)=1 и

 

 fla1(2×s)=2×fla1(s) - 1 (s³1). (16)

 

Аналогичные рассуждения показывают, что

 

 fla1(2×s+1)=2×fla1(s) + 1 (s³1). (17)

 

Величины fla1(n) назовем числами Флавия. Соотношения (16) и (17) сразу же позволяют написать следующую рекурсивную программу-функцию вычисления значений fla1(n).

 

 

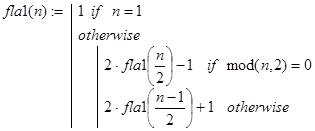
A2. Исследование рекуррентных соотношений (16)-(17) показывает, что

 

 fla1(2^s + q)=2×q+1 (s³0, 0£q<2×s) (18)

 

Отсюда получаем еще один рекурсивный алгоритм для вычисления чисел Флавия (см. ниже). При этом вспомогательная рекурсивная функция power(n,0) вычисляет значение s, удовлетворяющее соотношению (18), то есть уменьшенное на 1 количество цифр двоичного разложения n, а функция fla2(n) непосредственно вычисляет число Флавия для заданного n.

 

 

 

A3. Еще один способ нахождения чисел Флавия дается программой-функцией flavec(v), где v=(1 2 3 ... n)^T - вектор. Подавать такой вектор в качестве аргумента необязательно. Проще обращаться к flavec(v) c помощью функции fla3(n), где по заданному n генерируется соответствующий вектор v. Отметим, что в flavec(v) используется рекурсивный алгоритм непосредственного вычеркивания каждого второго числа. При этом вектор v перестраивается при каждом новом перемещении по кругу.

 

 

Контрольные примеры.

 

1. fla1(6)=5fla2(6)=5fla3(6)=5

2. fla1(11)=7 fla2(11)=7 fla3(11)=7

3. fla1(1000)=997fla2(1000)=997fla3(1000)=997