Вещественный корень f(x)

 

Задача 15. Пусть функция f(x) вещественной переменной x непрерывна на отрезке [a, b] и f(a)×f(b) £ 0. Составить программу нахождения на [a, b] какого-либо вещественного корня f(x).

Решение. Во первых, при перечисленных выше условиях по крайней мере один корень f(x) на [a, b] существует. Во вторых, договоримся о том, как понимать слова “найти корень”? Будем считать, что корень ищется с точностью e > 0, то есть должен быть найден отрезок [a, b] (b – a < 2×e), на котором корень имеется. Тогда в качестве приближенного значения корня может быть взята точка x₀ = (b + a)/2.

 Для отыскания решения многих задач часто используется метод дихотомии, называемый также методом последовательного деления пополам, бисекции или вилки. В некоторых ранее рассмотренных задачах мы уже сталкивались с этим методом. В нашем случае, когда ищется корень уравнения, суть его в следующем. Пусть e > 0 задано. Делим отрезок [a, b] точкой с=(b+a)/2 на две равные части и в качестве нового отрезка [a, b] берем ту из его половин, для которой снова f(a)×f(b) £ 0 и т.д. Ясно, что на некотором шаге будем иметь отрезок [a, b] такой, что b – a < 2×e и f(a)×f(b) £ 0. Следовательно, приближенное решение найдено и оно равно (b + a)/2.

А как записать предложенный алгоритм с использованием рекурсии? Оказывается все достаточно просто.

 

 

Контрольные примеры.

 

 1. y(x):= x³dicho(y, -1, 1, 0.01) = -0.008

2. f(u)=u×(u + sin(u) – 3)×exp(cos(u))

 dicho(f, 1, 3, 0.0001) = 2.18f(2.18)=0

 

Задача 16. Пусть функция f(x) вещественной переменной x непрерывна на отрезке [a, b]. Составить программу нахождения на [a, b] любого вещественного корня f(x). При отсутствии корней, должно быть выдано значение ¥ (10³⁰⁷).

Решение. Отличие постановки этой задачи от предыдущей в том, что здесь априори ничего неизвестно о знаках функции на концах отрезка и, следовательно, корней f(x) уже может и не быть. Однако метод дихотомии с успехом может быть применен и в данном случае. Соответствующий алгоритм может быть записан так.

 

 

Контрольные примеры.

Рассмотрим функции примеров из предыдущей задачи. Имеем:

 

 dichot(y,1,7,0.001)=10³⁰⁷ , dichot(f,2.17,3,0.0001)=2.18 .

Периодическое продолжение

 

Задача 17. Составить программу, которая для функции g(x), определенной при x Î [a,b), строит функцию peri(g,a,b,x), являющуюся периодическим продолжением g(x) на всю действительную ось c периодом w = b – a.

Решение. Нам, очевидно, требуется определить функцию следующего вида.

 

На языке Mathcad это будет выглядеть практически так же:

 

 

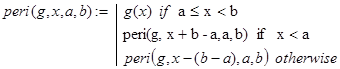
Заметим, что при x находящемся вдали от промежутка [a,b) вычисления значения функции peri() требует значительного количества рекурсивных вызовов. Происходит это по той причине, что за один такой вызов мы продвигаемся в направлении [a,b) лишь на расстояние w=b-a.

Значительно эффективней проводятся вычисления по функции F(g,x,a,b) также являющейся периодическим продолжением g(x) на всю числовую ось.

 

 

Контрольные примеры.

1. Пусть y(x) = x²×sin(x). Тогда:

 

peri(y,1,0,2) = 0.841 peri(y,3,0,2) = 0.841

peri(y,-1,0,2) = 0.841 peri(y,1001,0,2)=0.841

 

2. На рис. 3.4 изображен график функции H(t), являющейся периодическим продолжением функции y(x)= x²×sin(x) для x Î [-10, 0). H(t) построено с помощью программы-функции F(), а график выведен на промежутке [-10,20) с шагом h=0.1.

 t:= -10,-9.9..20 H(t):=perri(y,t,-10,0)

 

Рис. 3.4 Периодическое продолжение функции y(x)= x²×sin(x)

для x Î [-10, 0).

Функция Аккермана

Задача 18. Пусть n и m целые неотрицательные числа. Написать программу, вычисляющую классическую в теории рекурсии функцию Аккермана:

 

 (5)

 

Решение. Вычислить функцию Аккермана, исходя непосредственно из определения (5), удается лишь для некоторых малых n и m. Связано это со сложностью и необычностью рекурсивного определения. В общем случае не только ak() вычисляется через ak(), но и второй из аргументов функции также требует рекурсивного вызова ak(). Соответствующая программа-функция может быть записана так:

 

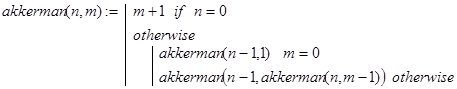
Контрольные примеры.

 

Следующий вариант программы для вычисления функции Аккермана включает в себя лишь один рекурсивный вызов:

 

 

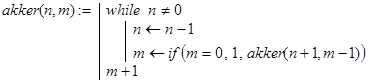
Замечание. Для m=0..4 справедливы соотношения [5, с. 69]:

 

 

Эти формулы могут оказаться полезными при построении контрольных примеров для отладки новых более эффективных вариантов программ вычисления функции Аккермана.

В работе [5, c. 256-260] приведен нерекурсивный вариант алгоритма вычисления значений функции Аккермана.

Функция Маккарти

Задача 19. Функция Маккарти. Показать, что для приведенной ниже рекурсивной программы-функции

 

 

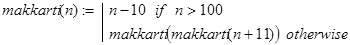
при целочисленных значениях n справедлива формула:

 

 (6)

 

 Решение. Относительно параметра n возможны три случая:

 

 n > 100,90£ n £100, -¥ < n<90.

 

В первом из них в силу базы рекурсии следует, что makkarti(n)=n-10. Во втором случае:

 

 

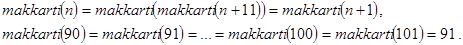
Наконец, всякое начальное n<90 в соответствии с декомпозицией через конечное число рекурсивных вызовов приводит ко второму случаю. Отсюда опять makkarti(n)=91. Таким образом (6) справедливо во всех случаях.

Заметим, что из проведенных рассуждений вытекает, что рассматриваемая функция может быть определена более просто, например, так:

 

 

Функция Кадью

 

Задача 20. Показать, что для приведенной ниже рекурсивной программы-функции

 

 

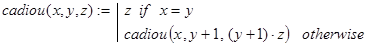
при целочисленных значениях x справедлива формула:

 

(7)

 

 Решение. При y=0 и z=1 имеем z=y!. Далее из характера декомпозиции функции cadiou() ясно, что z=y! остается инвариантом в ходе рекурсивных вызовов. Вместе с условием завершения x=y это и дает z=x! и (7) установлено.

Количество делителей

 

Задача 21. Количество делителей. Составить программу-функцию подсчета для натурального числа n количества всех его делителей.

Решение. Перейдем к более общей задаче. Подсчитаем для натурального числа n количества всех его делителей, меньших или равных заданному натуральному числу x. Пусть dn(n) и dnx(n,x) - соответственно функции для решения исходной и обобщенной задач. Очевидно, что dn(n)=dnx(n,n).

Рекурсивную функцию dnx(n,x), по которой последовательно подвергаются испытанию на делители n все числа от 1 до x включительно, можно определить так:

 

 

Контрольные примеры.

 

 

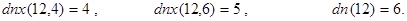
Далее, если n ³2 и dn(n)=2, то число n – простое. Однако проверка n на простоту этим способом весьма неэкономна.

Простые числа

Задача 22. Составить программу-функцию проверяющую, является ли заданное натурально число n простым?

Решение. Пусть рекурсивная функция isprim(n) является решением задачи и

 

Дальнейшие рассуждения являются иллюстрацией использования классического приема “вложения” (Дж. Маккарти, 1962). Перейдем к рассмотрению следующей обобщенной задачи. Пусть a , b , n - натуральные числа и 2 £ a £ b £ n . Верно ли, что заданное n не делится ни на одно целое из отрезка [ a , b ]? Пусть эту задачу решает функция

 

 

 

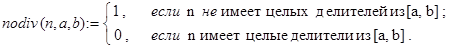
Ниже приведено три рекурсивных варианта реализации этой функции. По первому из них проверке на делитель n последовательно подвергаются числа: a, a+1, … , b; по второму - эти же числа в обратном порядке и, наконец, по третьему - a, b, a+1, b-1, … .

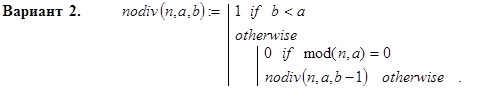
Контрольные примеры.

 

Далее, натуральное число n³2 является простым, если оно не имеет делителей на отрезке , поэтому характеристическая функция isprim(n) через функцию nodiv(n,a,b) может быть выражена так:

 

 

Контрольные примеры.

 

 

Задача 23. Составить программу-функциюpi(x), которая подсчитывает количество простых чисел, не превосходящих заданное число x.

Решение. С помощью функций nodiv() или isprim() рекурсивный вариант функции pi(x) строится достаточно просто, исходя из такого декомпозиционного утверждения. Количество простых чисел, не превосходящих x, составляется из количества простых чисел меньших или равных x-1 плюс значение функции isprim(x). Поэтому:

 

 

Контрольные примеры.

 

 

Задача 24. Составить программу pn(n), которая вычисляет n-ое простое число (n – натуральное).

 Решение. Предварительно напишем рекурсивную подпрограмму-функ-цию minp(m) нахождения наименьшего простого числа, большего или равного m (m – натуральное число). Сделать это можно, например, так:

 

 

Контрольные примеры.

 

 

Тогда искомая функция pn(n) может быть определена так:

 

 

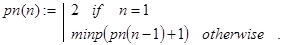
 Контрольные примеры.

 

 

Схема Горнера

 

Задача 25. Составить программу-функцию вычисления значений многочлена по схеме Горнера.

Решение. Пусть f(x) многочлен с вещественными или комплексными коэффициентами и v – вектор этих коэффициентов:

 

 (8)

 (9)

 

Вычисление f(x) в точке x по схеме Горнера проводится от самых внутренних скобок и далее в соответствии с представлением:

 

 

Отсюда ясно, как записать рекурсивный и не рекурсивный варианты алгоритмов вычисления f(x). Нас интересует только первый из них. Параметрами задачи можно считать вектор v и точку a для вычисления f(a). Тривиальный случай – многочлен нулевой степени: f(a) = a₀. Декомпозиция получается из указанной выше расстановки скобок в записи f(x). Соответствующая программа-функция выглядит, например, так.

 

 

Контрольные примеры.

 

 

Замечание. Параметр n – это константа, равная степени многочлена. По вектору v она определяется однозначно. Однако в каждом рекурсивном вызове проводится перевычисление n. Избежать лишней вычислительной работы в подобных ситуациях можно двумя способами. Или определять такие константы заранее вне текста программы-функции или передавать их значения через дополнительные аргументы функции.