Фактор - множество и разбиение.

Определение 1. Разбиением t множества A называется такое семейство t его непустых подмножеств A_i (пишем t = {A_i| iÎI} или t= = {A_i}, I - множество индексов), которое обладает двумя свойствами:

1) каждый элемент множества A принадлежит хотя бы одному из подмножеств A_i , iÎI;

2) ни один элемент множества A не принадлежит двум различным подмножествам A_i Î t.

Если t = {A_i} - разбиение множества, то подмножество A_i Î t называется классом разбиения.

Условия 1) и 2) определения 9.2 равносильны следующим двум:

1) объединение всех подмножеств A_i Î t равно A: ;

2) пересечение различных подмножеств A_i Î t пусто: если A_i ¹ A_j , то A_i Ç A_j = Æ для любых i , j ÎI.

Примеры . 1. Пусть A = {1, 2, 3, 4, 5, 6, 7}, A₁ = {1, 4, 7}, A₂ = {2, 5},  A₃ = {3, 6}. Тогда t = {A₁, A₂, A₃}- разбиение множества A.

2. Пусть A - множество всех учеников первых классов школы № 1 г. Череповца; A₁, A₂, A₃, A₄, A₅ - множества учеников соответственно 1а, 1б, 1г, 1в, 1д классов этой школы (других первых классов в школе № 1 нет). Тогда  t = {A₁, A₂, A₃, A₄, A₅} - разбиение множества A.

Установим связь разбиений с отношениями эквивалентности.

Определение 2. Пусть - отношение эквивалентности на множестве A . Фактор множеством множества A по отношению эквивалентности  называется множество, обозначаемое  и состоящее из всех классов эквивалентности по отношению : .

Примеры. 3. Пусть || - отношение параллельности на множестве A прямых плоскости (см. примеры 8.1, 9.1). Тогда 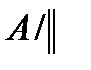- множество всех пучков параллельных прямых плоскости.

3. Пусть - отношение эквивалентности, рассмотренное в примерах 4.4. Здесь имеется только три класса эквивалентности:  и .

Последний пример интересен тем, что фактор множество совпадает с разбиением из примера 10.1. Оказывается это не случайно. Имеют место следующие две теоремы.

Теорема 1. Пусть - отношение эквивалентности на множестве A . Тогда фактор множество  есть разбиение множества A .

Доказательство. Рассмотрим множество . По теореме 9.1 каждый класс эквивалентности не пуст. По той же теореме каждый элемент aÎA принадлежит хотя бы одному из классов эквивалентности, а именно . Поэтому условие 1) определения 1 выполняется.

По теореме 4.3, ни какой элемент из A не принадлежит двум различным классам эквивалентности. Поэтому условие 2) определения 1 тоже выполняется.

Следовательно, - разбиение множества. 

Теорема 2. Пусть t = {A_i| iÎI} - разбиение множества, бинарное отношение t ^* на множестве A определяется формулой:

.

Тогда t ^* является отношением эквивалентности на множестве A и при этом фактор множество совпадает с разбиением t : .

Доказательство. 1. Из определения t ^* следует, что t ^* рефлексивно, симметрично, транзитивно и поэтому t ^* является отношением эквивалентности на A.

3. Докажем теперь, что если aÎ A_i, то = A_i.

Пусть xÎ . Тогда по определению класса эквивалентности x t ^* a. Следовательно, по определению t ^* существует такой класс разбиения A_jÎt , что x , aÎA_j,. Тогда aÎ A_i, aÎA_j. Но, по определению разбиения, разные классы эквивалентности не пересекаются. Поэтому A_i = A_j и xÎ A_i.

Обратно, пусть yÎ A_i. Так как aÎ A_i, то, по определению t ^*, y t ^* a. Тогда по определению класса эквивалентности xÎ .

Таким образом, по определению равенства множеств = A_i.

4. Наконец докажем, что .

Пусть . По определению разбиения для элемента a существует хотя бы один такой класс разбиения A_i Ît, что aÎ A_i. Тогда по 2-й части доказательства = A_i и, отсюда Ît.

Обратно, пусть A_i Ît. Так как A_i ¹ Æ, то имеется хотя бы один элемент aÎ A_i (который принадлежит также ). Тогда по 2-й части доказательства = A_i и .

Следовательно, по определению равенства множеств .

Упражнения:1. Пусть arb Û ab > 0, a, bÎR\{0}. Доказать, что r отношение эквивалентности на R\{0} и найти его классы эквивалентности.

 

Отношение порядка

Определение 1. Бинарное отношение r на множестве A называется отношением порядка, а множество A - упорядоченным, если оно антисимметрично и транзитивно.

Определение 2. Отношение порядка r на множестве A называется отношением строгого порядка, а множество A - строго упорядоченным, если оно антирефлексивно.

Определение 3. Отношение порядка r на множестве A называется отношением нестрогого порядка, а множество A - нестрого упорядоченным, если оно рефлексивно.

Определение 4. Отношение порядка r на множестве A называется отношением линейного порядка, а множество A - линейно упорядоченным, если для любых двух элементов a , bÎA выполняется хотя бы одно из двух a r b или b r a.

Отношение порядка r на A, которое не является линейным, называется частичным порядком, множество называется частично упорядоченным. 

Обычно отношение строго порядка обозначается символами "<" или ">" и читается соответственно "меньше" или "больше", отношение нестрого порядка обозначается символами "£" или "³" и читается соответственно "меньше или равно" или "больше или равно". Тогда определению 14.2 можно записать в следующем виде.

Определение 2 ¢ . Бинарное отношение £ на множестве A называется отношением нестрогого порядка, если

1) "(a ÎA) [a £ a],

2) "(a, b ÎA) [a £ b & b £ a Þ a = b],

3) "(a, b, c ÎA) [(a £ b) & (b £ c) Þ a £ c].

Определение 3 ¢ . Бинарное отношение £ на множестве A называется отношением строгого порядка, если

1) "(a ÎA) [a < a Þ aÎÆ],

2)  "(a, b ÎA) [a < b & b < a Þ a = b],

3) "(a, b, c ÎA) [(a < b) & (b < c) Þ a < c].

Первое свойство в определении 3' равносильно условию антирефлексивности.

На рис. 8-10 изображены графы соответственно частичного не линейно упорядоченного, нестрого не линейно упорядоченного, строго не линейно упорядоченного множеств, а на рис. 11-13 то же, но множества линейно упорядочены. 

4

1

1

1

2

2

2

3

3

4

4

3

Рис. 8

Рис. 9

Рис. 10

1

1

1

2

4

2

2

3

3

4

4

3

Рис. 11

Рис. 12

Рис. 13

1

Примеры. 1. Пусть U - некоторое множество, P(U) - множество всех его подмножеств. Рассмотрим на A = P(U) отношение включения Í. По теоремам 1.1 и 1.3, отношение Í - отношение порядка на A. Этот порядок в случае, когда множество имеет более одного элемента не линейный (проверить).

2. Пусть A = N (множество натуральных чисел). Рассмотрим на A отношение a|b(a делит b). Справедливы свойства:

1) любое натуральное число a делит само себя (рефлексивность);

2) если a делит b и b делит a, то a = b (антисимметричность);

3) если a делит b и b делит c, a то c (транзитивность).

Таким образом, отношение "делит" упорядочивает множество N. Этот порядок - частичный (не линейный), так как, например, 3 не делит 2 и 2 не делит 3.

4. Обычное отношение £ на множестве действительных чисел является отношением линейного порядка.

5. Отношение "делит" есть отношение частичного порядка на множестве A = {1, 2, 3, 4, 6, 12}, элементы которого - все натуральные делители числа 12.

Если a и b - элементы частично упорядоченного множества A. Говорят, что b накрывает a, если a < b и не существует такого элемента с Î A с условием: a < c < b. Если множество A конечно, то a < b тогда и только тогда, когда существует такая цепочка элементов a < a₁ < a₂ <…. < a_n = b , в которой a_i накрывает a_i-1.

Последнее понятие удобно использовать при изображении частично упорядоченных множеств A в виде плоских диаграмм точками. Если b накрывает a, то b располагаем выше a и соединяем b и a прямолинейным отрезком. Если a < b, то b и a соединяются "спадающей" ломаной, соединяющей b и a. Не сравнимые a и b, для которых a и b не связаны отношением £, ломаными не соединяются.

На рис. 14 изображается множество {1, 2, 3, 4, 5, 6, 7}, упорядоченное обычным отношением ; на рис. 15 – множество P ( A ), A ={a , b , c}, упорядоченное отношением Í; на рис. 16 - множество из примера 5 , упорядоченное отношением "делит".

Определение 5. Элемент m упорядоченного множества A называется минимальным (максимальным), если во множестве A не существует элемента, меньшего (большего) m.

Например, на диаграммах 8-10 множество имеет один минимальный и два максимальных элемента

Теорема 1. Любое конечное, непустое, частично упорядоченное множество имеет минимальный и максимальный элементы.

Доказательство. См. ТУ 5.

Определение 5. Пусть B - подмножество частично упорядоченного множества A . Если существует такой элемент m Î A, что для всех b Î B имеем b £ m, то он называется верхней границей множества B , а множество B называется ограниченным сверху. Если существует такой элемент к Î A, что для всех b Î B имеем к £ b, то он называется нижней границей множества B , а множество B называется ограниченным снизу.

Определение 6. Если верхняя граница множества B принадлежит множеству B , то она называется максимумом множества B и обозначается символом Max B. Если нижняя граница множества B принадлежит множеству B , то она называется минимумом множества B и обозначается символом Min B.

Определение 7. Наименьшая из всех верхних границ множества B (если она существует) называется точной верхней границей множества B и обозначается символом Sup B. Наибольшая из всех нижних границ множества B (если она существует) называется точной нижней границей множества B и обозначается символом Inf B.

Изображенные на рис 14, 15, 16 множества являются ограниченными снизу и сверху, имеют максимумы и минимумы. Например, для множества A, изображенного на рис. 1.31, Max B = Sup B = 12, Min B = Inf B =1.

{c}

{ b}

{a }

{a,b,c}

{a,b}

{a,b}

{a,b}

6

4

3

1

1

2

12

1

2

3

4

5

6

7

Рис. 14

Рис. 15

Рис. 16

Æ

Упражнения: 1. Является ли отношение сравнимости действительных чисел по модулю отношением порядка.

2. Перечислить все отношения порядка на множестве {1, 2, 3} и построить их графы. Сколько отношений порядка каждого вида существует?

3. Построить линейный порядок на множестве N ².

4. Доказать, что сужение отношения порядка является отношением порядка.

5. Доказать теорему 1.

6. Доказать, что любое частично упорядоченное конечное множество можно вполне упорядочить, сохраняя на нем частичный порядок.