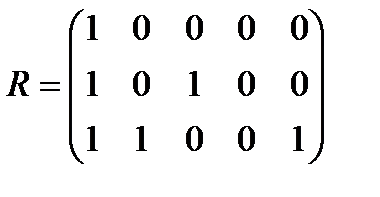Бинарные отношения и способы их задания. Матрица отношений. Граф отношения

Алгебра и теория чисел

Толстиков А.В.

Курс 1 . Семестр 1 . Лекция 2.

Бинарные отношения и оттображения

План

1. Бинарные отношения и способы их задания. Матрица отношений. Граф отношения.

2. Алгебра отношений. Обратное бинарное отношение. Композиция бинарных отношений.

1. Отношение эквивалентности.
2. Классы эквивалентности.
3. Отношение порядка Функциональные отношения. Отображения.
4. Виды отображений.
5. Обратное отображение.

 

 

Литература.

1. Данилов А.Н., Толстиков А.В. Вводные главы алгебры и математического анализа. –Вологда, 1986. –С. 24-36.

2. Куликов Л.Я. Алгебра и теория чисел. -М.: Высшая школа, 1978. –С. 48-54.

5. Ляпин Е.С. Алгебра и теория чисел. -М.:Просвещение, 1974. –С. 11-18.

4. Биргоф Г., Барти Т. Современная прикладная алгебра. - М.: Мир, 1976. –С. 39-54.

5. Матрос Д.Ш., Поднебесная Г.Б. Элементы абстрактной и компьютерной алгебры. -М.:Изд. центр Акдемия, 2004. -С. 9-12.

 

 

Бинарные отношения и способы их задания. Матрица отношений. Граф отношения

Определение 1. Бинарным отношением между элементами множеств A и B называется любое подмножество r декартова произведения A´B: r Í A´B.

Бинарное отношение обозначается тройкой множеств (A, B, r), или одним символом r , если известно о каких множествах A и B идет речь. Бинарное отношение r Í A´B называется также соответствием между множествами A и B .

Подмножества r =Æ и r=A´B называются соответственно пустым и универсальным бинарными отношениями между элементами множеств A и B .

По определению бинарное отношение r состоит из пар, если (a , b) Î r , то говорят, что элементы находятся в отношении r или связаны отношением r . Вместо записи (a , b) Î r используется также запись a r b.

Множество всех первых компонент a пар (a , b) Î r называется областью определения бинарного отношения r и обозначается символом D(r). Множество всех вторых компонент b пар (a , b) Î r называется областью значений бинарного отношения r и обозначается символом E(r).

Бинарное отношение считается заданным, если указана тройка множеств (A, B, r), где r Í A´B. Используются следующие способы задания бинарных отношений.

1. Перечислением пар, входящих в бинарное отношение.

Пример 1. A = {1, 2, 3}, B = {4, 6}, r  = {(2, 4), (3, 6)}.

2. Указанием характеристического свойства, которым обладают пары, входящие в бинарное отношение.

Пример 2. A = {2, 4, 6}, B = {2, 3, 4, 5, 6}, r  = {(a, b)½aÎB, bÎA, a делится на b}.

3.  Табличный способ. При табличном представлении бинарного отношения r Í A´B строят таблицу, обозначая ее столбцы элементами множества B, а строки - элементами множества A. В таблице отмечают те пары элементов, которые находятся в отношении r.

Например, табличное представление отношения из примера 5.2 имеет вид:

B

A

	2	3	4	5	6
2	+
4	+		+
6	+	+			+

Если множество A = (a₁, a₂,… , a_n) имеет n элементов, а множество B = (b₁, b₂,… , b_m) - m элементов, то бинарное отношение r задается в виде матрицы R = (r_ij) размерности n´m (таблицы), которая состоит из нулей и единиц и называется матрицей бинарного отношения. При этом r_ij = 1 тогда и только тогда, когда (a_i, b_j) Îr. Например, для указанного выше бинарного отношения r, указанна матрица R отношения.

2

44

3

5

6

A

4

6

2

B

r

Рис. 1

4. Представление бинарного отношения орграфом (стрелками). Отметим, что орграфом называется плоская фигура, состоящая из конечного числа точек - вершин (узлов) орграфа и линий, соединяющих некоторые из его вершин и называемых дугами орграфа.

Для изображения бинарного отношения rÍA´B между элементами конечных множеств A и B в виде орграфа элементы множеств A и B изображаются точками плоскости, а пары (a , b)Î r изображаются стрелками, соединяющими точки a и b .

-3

y

x

3

3

-3

0

Рис. 2

Например, представление в виде графа отношения из примера 2 изображено на Рис. 1.

 5. Графическийспособ задания бинарных отношений. Пусть rÍA´B , где A Í R , B Í R. На плоскости выберерем прямоугольная система координат xOy, на осях Ox и Oy изображаем соответственно множества A и B. Пары (a , b)Î r изображаются точками плоскости xOy с координатами (a , b). Множество точек плоскости называется графиком бинарного отношения rÍA´B.

Например, бинарное отношение r  = {(x , y)½xÎA , yÎB, x² + y² = 9}, A = R , B = R, изображается графически окружностью (см. Рис. 2).