Определение 1. Отображение f множества X в Y называется отображением множества X на Y,
или сюръективным, или сюръекцией, если для любого yÎ
Y найдется такой элемент xÎ
X,
что f(
x) =
y .
Таким образом, f: X®Y сюръекция тогда и только тогда, когда E(f) = Y .
Например, отображение f: R®[0, +¥), f: xax2, является сюръекцией, см. также рис. 6, 7 . Отметим, что отображения на рис 2, 3 не являются таковыми.
Определение 2. Отображение f множества X в Y называется взаимно однозначным отображением множества X в Y , или инъективным, или инъекцией, или вложением, если для любых x1, x2 Î X из x1 ¹ x2 следует, что f(x1) ¹ f(x2).
Например, отображение
f:
R\{0}®
R,
f:
xa1/
x, является инъекцией, см. также рис. 7, 8, 9. Отметим, что отображения на рис.2,3 , 6 не являются таковыми.
Определение 3. Отображение f множества X в Y называется взаимно однозначным отображением множества X на Y , или биективным, или биекцией, если оно одновременно сюръективно и инъективно.
Иными словами биективное отображение взаимно однозначно и является отображением X на Y. Взаимно однозначное отображение множества X на Y обозначается также символом f: X«Y .
В геометрии взаимно однозначные отображения множества X на себя называются преобразованиями множества. В математическом анализе взаимно однозначные отображения множества X на Y называются взаимно однозначными соответствиями между X и Y.
Например, отображение f: (0,+¥)®R, f: xalg x, является биекцией, см. также рис. 7., 9. Отметим, что отображения на рис 1., 1., 6., 8 не являются таковыми.
Теорема 1. 1. Композиция  двух сюръекций f и g есть сюръекция.
двух сюръекций f и g есть сюръекция.
2. Композиция  двух инъекций f и g - инъекция.
двух инъекций f и g - инъекция.
3. Композиция  двух биекций f и g - биекция.
двух биекций f и g - биекция.
Доказательство. Композиция  двух отображений f: X®Y , g: Y®W есть отображение X®W. Если f и g сюръекции, то f(X) = Y , g(Y) = W. Поэтому
двух отображений f: X®Y , g: Y®W есть отображение X®W. Если f и g сюръекции, то f(X) = Y , g(Y) = W. Поэтому  и
и  - сюръекция.
- сюръекция.
Пусть x1, x2 Î X и x1 ¹ x2. Пусть f и g инъекции. Тогда f(x1) ¹ f(x2). Отсюда 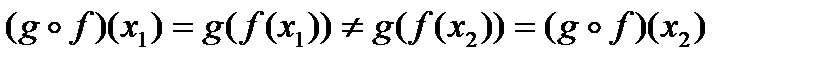 и
и  - инъекция.
- инъекция.
Третье утверждение теоремы следует из первых двух по определению 3.
8. Обратное отображение
Определение 1. Отображение f: X®Y называется обратимым, если обратное для его бинарное отношение f -1 является отображением множества Y в X. Тогда обратное бинарное отношение f -1 называется обратным отображением для отображения f и обозначается тем же символом f -1.
Например, для отображения
f: (0,+¥)®
R,
f:
xalg
x, обратное отображение
f -1:
R®(0, +¥),
f -1:
xa10
x. Отображения на рис. 7. и 9 обратимы (см. также рис. 10).
Отметим, что не каждое отображение обратимо. Например, отображения представленные на рис. 6., 8 не обратимы.
Теорема 1. Пусть отображение f: X®Y - обратимо, f -1 – обратное отображение. Тогда y = f(x) тогда и только тогда, когда x = f -1(y) для любых xÎ X и yÎ Y .
Доказательство. По определению обратного бинарного отношения (x, y) Î f тогда и только тогда, когда (y, x) Î f -1 . В силу обозначений из этого следует утверждение теоремы.
Теорема 2. Пусть отображение f: X®Y - обратимо. Тогда 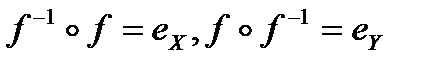 .
.
Доказательство. Следует из определений 5, 6 и теоремы 2.
Теорема 3. Отображение f: X®Y - обратимо тогда и только тогда, когда оно биективно.
Доказательство. (Þ) Пусть отображение f: X®Y обратимо и f -1: Y®X обратное ему отображение. По определению отображения для любого y Î Y существует единственный элемент xÎ X такой, что x = f -1(y) и по теореме 2 y = f(x). По определению 2.1 f - сюръекция.
Доказывая, что f биекция предположим противное. Пусть найдутся такие два элемента x1, x2 Î X , x1 ¹ x2 , что f(x1) = f(x2), y1= f(x1), y2= f(x2). Тогда y1 = y2 и по теореме 2 x1= f -1(y1) = f -1(y2) = x2, а это противоречит предположению.
(Ü) Пусть отображение f: X®Y - биективно, f -1 - обратное бинарное отношение для f. По определению 2.1 для каждого y Î Y существует такой элемент xÎX, что y = f(x), т.е. такой, что (y, x)Îf -1. Покажем, что такой элемент xÎ X единственный. Действительно, допустим, что существуют два такие элемента x1, x2 Î X , x1 ¹ x2 , (y, x1)Îf -1, (y, x2)Îf -1. Тогда по определению обратного бинарного отношения (x1, y)Îf , (x2, y)Îf и f(x1) = y = f(x2), а это противоречит тому, что f - биективно.
Если f -1: Y ® X обратное отображение для отображения f: X®Y, то область определения Y отображения f -1 равна множеству значений отображения f, D(f -1) = E(f), и наоборот E(f -1) = D(f). Если области определений отображений f и f -1 изображаются на оси Ox, то графики этих отображений симметричны относительно биссектрисы первого и второго координатных углов, т.е. относительно прямой y==x .
Например, для функции sin: [-p/2,p/2]®[-1,1] обратной является функция arcsin: [-1,1]® [-p/2,p/2]. По теореме 3 для любых xÎ[-p/2,p/2]и yÎ[-1,1] справедливы тождества arcsin(sin x) = x и sin(arcsin y) = y.
Упражнения: 1. Даны функции cos x, tg x, ctg x, x2, log2 x . Какие из этих функций являются отображениями R в R , сюръекциями, инъекциями, биекциями?
Сузить их области отправления и прибытия так, чтобы они стали обратимыми, найти обратные функции и построить их графики.
В каждом случае написать тождества теоремы 3.4.
3.2. Доказать теорему 3.3.
3.3. Доказать, что графики функций y = f(x) и y = f-1(x) симметричны относительно прямой y = x.

 двух сюръекций f и g есть сюръекция.
двух сюръекций f и g есть сюръекция. двух инъекций f и g - инъекция.
двух инъекций f и g - инъекция. двух биекций f и g - биекция.
двух биекций f и g - биекция. двух отображений f: X®Y , g: Y®W есть отображение X®W. Если f и g сюръекции, то f(X) = Y , g(Y) = W. Поэтому
двух отображений f: X®Y , g: Y®W есть отображение X®W. Если f и g сюръекции, то f(X) = Y , g(Y) = W. Поэтому  и
и  - сюръекция.
- сюръекция.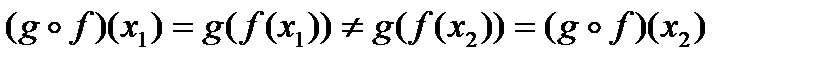 и
и  - инъекция.
- инъекция.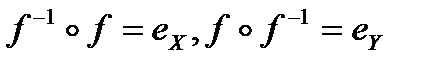 .
.

