ПОСТАНОВКА ЗАДАЧ РАСЧЕТА ЭЛЕКТРОМАГНИТНОГО ПОЛЯ ЭЛЕКТРОТЕХНИЧЕСКОГО УСТРОЙСТВА

Математическим описанием непрерывных в пространстве и во времени процессов распределения тепла, электромагнитного поля, полей механических деформаций в технических объектах и системах являются дифференциальные уравнения в частных производных (уравнения математической физики). Различают стационарные (не меняющиеся во времени) и нестационарные (переменные, меняющиеся во времени) процессы. Стационарные процессы описываются эллиптическими уравнениями, а нестационарные – уравнениями параболического и гиперболического типов.

Эти уравнения для электромагнитных полей относительно характеристик поля (векторов напряженности электрического и магнитного полей  и ; векторов электрической и магнитной индукции 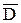 и ; векторного магнитного потенциала , скалярного электрического потенциала j) получают из преобразования уравнений Максвелла [3, 4, 5, 36], описывающих электромагнитные процессы ЭУ. Уравнения Максвелла

                       ,                                                                             

                              ,                                                                                   

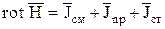                              div  = 0,                                                                                                

                              div  = r,                                                                                            

                              ,                                                                                               

                          ,                                                                                         

                              ,                                                                            

где - вектор плотности сторонних токов;  - вектор плотности тока проводимости, вызванного в проводящей среде изменением электромагнитного поля во времени и движением в ней этой среды со скоростью ;  =  - вектор плотности тока электрического смещения; m и e - относительная магнитная и диэлектрическая проницаемости материала; m0 = 4p×10-7 Гн/м - магнитная постоянная; e0 = 8,85×10-12 Ф/м - электрическая постоянная; g - удельная электрическая проводимость; r - объемная плотность заряда.

Уравнения Максвелла дополняются уравнениями, связывающими основные силовые характеристики поля с их потенциалами: = rot , = - grad j_эм и   = - grad j.

Система уравнений Максвелла совместно с краевыми условиями на внешних границах и условиями сопряжения на внутренних границах расчетной области представляет собой модель электромагнитного поля электротехнического устройства и позволяет однозначно определять в каждой точке пространства в любой момент времени значения векторов , ,  и  при заданных начальных данных в момент времени t0.

Стационарные задачи

Наиболее часто используемые эллиптические уравнения – это уравнения Лапласа и Пуассона, которыми в теории электромагнетизма описываются задачи электростатики и магнитостатики. Простейшим эллиптическим уравнением является уравнение Лапласа

                                                Du =0,

где лапласиан (оператор Лапласа) D = . Этот оператор может быть применен к скалярным и векторным функциям. В декартовой системе координат (рис. 1.1)  уравнение Лапласа имеет вид

                    = 0,

где j (x, y, z) – скалярная функция.

Рис. 1.1 Декартова и цилиндрическая система координат

В цилиндрической системе координат (рис. 6.1) оно выглядит следующим образом:

                 = 0,

где j (R, a, z) [17].

Уравнением Dj = 0 описывается электростатическое поле в диэлектрике либо электрическое поле постоянного тока, и j - скалярный потенциал электрического поля.

К уравнениям эллиптического типа относится уравнение Пуассона, которое для линейных изотропных (m_х = m_y = m_z = m = const) сред имеет вид:

                            ,

где  - векторный магнитный потенциал (ВМП), 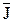 - вектор плотности тока,       m_а = mm₀ - абсолютная магнитная проницаемость среды моделирования.

Если речь идет о нелинейных средах моделирования, т.е. m ¹ const, то из уравнений Максвелла получим 

                              rot

или

                 .

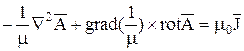Вектор-потенциал  есть величина векторная и в декартовой системе координат , вектор плотности тока . Тогда уравнение Пуассона разбивается на три уравнения относительно скалярных величины А_x, А_y, А_z:

                                        ,

                                            ,

                                            .

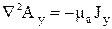Если в модели ЭУ принять, что ток, а следовательно, и векторный магнитный потенциал имеют только z-составляющую, то получим плоскопараллельную или осесимметричную задачу. Для плоскопараллельного магнитного поля в декартовой системе координат можно записать уравнение Пуассона

                                   .

Решив данное уравнение и зная распределение векторного магнитного потенциала по области моделирования, можно найти распределение составляющих вектора магнитной индукции и результирующего значения (модуля) вектора магнитной индукции по выражениям

                               B_x = ¶A_z/¶y; B_y = - ¶A_z/¶x; B_r= ,

полученным из нижеследующего выражения

                                      .

Для того чтобы уравнения Лапласа-Пуассона имели единственное решение, они дополняются граничными (краевыми) условиями. На замкнутой границе Г модели ЭУ могут быть заданы следующие краевые условия [32].

1. Граничные условия первого рода (Дирихле) – на границе Г задается значение искомой функции, т.е. j = f₁ (x, y, z), где точки с декартовыми координатами (x, y, z) принадлежат границе Г. Условие j = 0 является однородным.

2. Граничные условия второго рода (Неймана). Для них задается изменение искомой функции по нормали  к границе Г, т.е dj /dn= f₂ (x, y, z), где точки с координатами (x, y, z) принадлежат границе Г. Условие dj/dn = 0 является однородным.

3. Граничные условия третьего рода dj /dn + f₃ (j) = f₄ (x, y, z), где точки с координатами (x, y, z) принадлежат границе Г.

На границе модели могут быть заданы смешанные краевые условия, т.е. сочетание вышеприведенных – первого, второго и третьего рода.