Двумерный симплекс-элемент

Метод конечных элементов основан на аппроксимации непрерывной функции (потенциала, температуры и т.д.) дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей, которые называются конечными элементами. В качестве функции элемента чаще всего используется полином. Классификацию КЭ можно провести в соответствии с порядком этих полиномов. Рассматриваются три группы элементов: симплекс-, комплекс- и мультиплекс-элементы [13, 33].

Симплекс-элементам соответствуют полиномы содержащие константу и линейные члены. Полином

представляет собой симплексную функцию для двумерного треугольника с тремя узлами.

Комплекс-элементам соответствуют полиномы, содержащие константу, линейные члены, а также члены второго и более высокого порядка. Форма комплекс-элемента может быть такой же как и форма симплекс-элемента (например, треугольник), но комплекс-элементы имеют дополнительные граничные узлы. Интерполяционный полином для треугольного комплекс-элемента с шестью узлами (три промежуточных на трех сторонах) имеет вид

                  + .

Для мультиплекс-элементов также используются полиномы с членами высокого порядка, но их границы должны быть параллельны координатным осям, что необходимо для достижения непрерывности при переходе от одного элемента к другому. Классический пример такого КЭ – прямоугольник. Границы симплекс- и комплекс-элементов не имеют таких ограничений.

Двумерный симплекс-элемент показан на рис. 1.2. Классическое его описание приведено в [33]. Это треугольник с прямолинейными сторонами и тремя узлами, по одному в каждой вершине. Как правило, используется последовательная нумерация узлов против часовой стрелки, начиная от некоторого i-го узла, который выбирается произвольно. Узловые значения скалярной величины  обозначаются через ,  и , а координаты трех узлов - через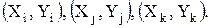

Интерполяционный полином имеет вид

                                                                       (1.1)

Рис. 1.2. Двумерный симплекс-элемент

В узлах выполняются следующие условия:

                          при , ,

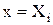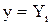                          при , ,

                    при , .

Подстановка этих условий в формулу (1) приводит к системе уравнений

                                   ,

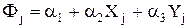                         ,                                 (1.2)                   

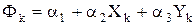                         ,                                                     решая которую, получаем

,

,

.                    

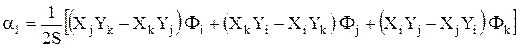Определитель системы связан с площадью треугольника S соотношением

                              .                                           (1.3)
 Подставляя значения ,  и 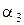 в (1.1), можно преобразовать выражение для  к виду:

 = [N_i, N_j, N_k] 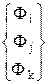= ,            (1.4)

где m = i, j, k – номера узлов. Для каждого узла функция формы (пробная функция) выглядит следующим образом:

     ,

     ,

      ,                         

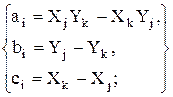
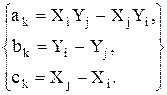
Вычислим значение  в i-м узле:

    .    Выражение в скобках представляет собой величину определителя в формуле (1.3), поэтому в узле с номером i

                                    (2S) = 1.                                        

Можно доказать, что  равно нулю во втором и третьем узлах, так же как и во всех точках прямой, проведенной через эти узлы.

Скалярная величина  определяется внутри элемента функциями формы, линейными по x и y. Это означает, что градиенты этой величины в направлениях x и y будут постоянны. Градиент в направлении x определяется соотношением

                        ,   (1.5)  

но

               ,      ,                                                          

поэтому

                                 . (1.6)
Так как для КЭ , ,  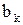- постоянны (они фиксированы, как только заданы узловые координаты) и , , - это узловые значения искомой функции j, которые не зависят от координат пространства, частная производная в формуле (1.6) имеет постоянное значение по элементу. Постоянство градиента внутри каждого элемента означает, что необходимо использовать очень малые по величине элементы, чтобы аппроксимировать быстро меняющуюся функцию .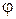

Следует отметить два полезных свойства треугольного симплекс-элемента. Первое свойство заключается в том, что функция 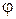 изменяется линейно между двумя любыми узлами. Так как узлы определяют границы элемента,  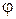меняется линейно вдоль каждой из трех его сторон. Отсюда следует второе полезное свойство: любая линия, вдоль которой  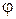принимает одинаковые значения, есть прямая, пересекающая две стороны элемента. Исключением будет случай, когда во всех узлах значения  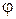одинаковые. Приведенные два свойства позволяют легко определять линии уровня скалярной величины внутри КЭ.