 |
Главная |
Уравнения метода конечных элементов.
|
из
5.00
|
Задачи теории поля
Задачи теории поля описываются дифференциальными уравнениями в частных производных. Дифференциальное уравнение для каждого из таких физических процессов представляется квазистационарным уравнением [33] в декартовой системе координат
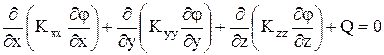 (1.7)
(1.7)
с граничными условиями 

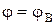 на
на 
и (или)
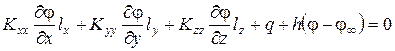 (1.8)
(1.8)
на 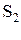 . Объединение
. Объединение 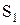 и
и 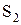 образует полную границу модели. Коэффициенты
образует полную границу модели. Коэффициенты 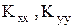 и
и 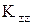 , а также величина q могут быть функциями x, y и z, но предполагаются независимыми от
, а также величина q могут быть функциями x, y и z, но предполагаются независимыми от 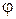 . Величины lx, ly и lz в формуле (1.8) - направляющие косинусы вектора нормали к поверхности модели. Уравнение (1.7) применимо как к изотропным, так и к анизотропным телам. Координатные оси, однако, должны быть параллельны главным осям инерции в анизотропных областях.
. Величины lx, ly и lz в формуле (1.8) - направляющие косинусы вектора нормали к поверхности модели. Уравнение (1.7) применимо как к изотропным, так и к анизотропным телам. Координатные оси, однако, должны быть параллельны главным осям инерции в анизотропных областях.
Уравнение для одномерного и двумерного случаев может быть получено из формулы (1.7) с учетом того, что 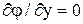 и (или)
и (или) 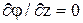 . Если на той части границы, где
. Если на той части границы, где 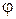 не определено (на
не определено (на 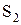 ), обе величины q и h равны нулю, равенство (1.8) сводится к следующему условию:
), обе величины q и h равны нулю, равенство (1.8) сводится к следующему условию:
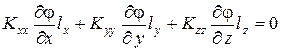 .
.
Важной двумерной задачей является задача о безвихревом течении жидкости. В этом случае 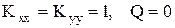 и уравнение (1.7) сводится к уравнению:
и уравнение (1.7) сводится к уравнению:
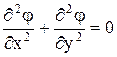 (1.9)
(1.9)
с граничными условиями 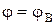 и
и 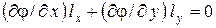 . Если полевая функция
. Если полевая функция 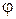 задана на непроницаемых границах области (на границах, по нормали к которым не происходит течения жидкости), то уравнение (1.9) определяет линии тока при безвихревом течении жидкости. С другой стороны, если полевая функция определена на тех частях границы, по нормали к которым течет жидкость, то уравнение (1.9) описывает эквипотенциальные линии, которые ортогональны линиям тока.
задана на непроницаемых границах области (на границах, по нормали к которым не происходит течения жидкости), то уравнение (1.9) определяет линии тока при безвихревом течении жидкости. С другой стороны, если полевая функция определена на тех частях границы, по нормали к которым течет жидкость, то уравнение (1.9) описывает эквипотенциальные линии, которые ортогональны линиям тока.
Дифференциальное уравнение для ограниченного потока грунтовых вод также содержится в уравнении (1.7). В этом случае
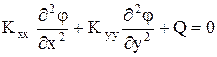 ,
,
а граничные условия имеют вид 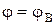 и (или)
и (или)
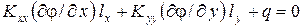 .
.
Коэффициенты 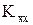 и
и 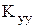 определяют проницаемость почвы, Q-источник (или сток) воды, а полевая функция
определяют проницаемость почвы, Q-источник (или сток) воды, а полевая функция 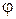 - пьезометрический напор. Величина q соответствует просачиванию воды через водоносный слой вдоль части его границы.
- пьезометрический напор. Величина q соответствует просачиванию воды через водоносный слой вдоль части его границы.
Другие важные физические задачи, которые описываются уравнением (1.7), связаны с рассмотрением электростатического и магнитостатического полей.
С вариационной точки зрения решение уравнения (1.7) с граничными условиями (1.8) эквивалентно нахождению минимума функционала [33]:
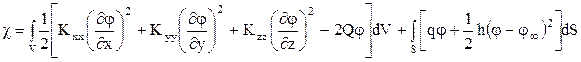 . (1.10) Минимизация функционала (6.10) должна быть осуществлена на множестве узловых значений {Ф} . Введем две матрицы:
. (1.10) Минимизация функционала (6.10) должна быть осуществлена на множестве узловых значений {Ф} . Введем две матрицы:
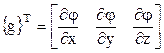 (1.11)
(1.11)
и
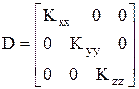 (1.12) Соотношение (6.10) может быть теперь записано в виде
(1.12) Соотношение (6.10) может быть теперь записано в виде
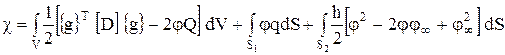 (1.13)
(1.13)
Так как функции от 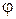 не являются непрерывными во всей области, вместо них введем в рассмотрение функции
не являются непрерывными во всей области, вместо них введем в рассмотрение функции 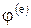 , определенные на отдельных конечных элементах. Интегралы в (6.13) разбиваются на интегралы по отдельным элементам, что дает сумму
, определенные на отдельных конечных элементах. Интегралы в (6.13) разбиваются на интегралы по отдельным элементам, что дает сумму
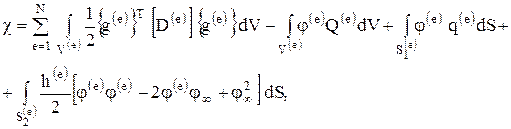 (1.14)
(1.14)
где N - общее число элементов. Последнее соотношение может быть символически записано как
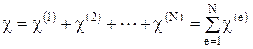 ,
,
где 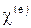 - вклад отдельного элемента в
- вклад отдельного элемента в 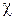 . Минимизация
. Минимизация 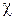 требует выполнения соотношения
требует выполнения соотношения
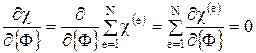 . (6.15)
. (6.15)
Учитывая соотношение (4):
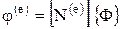 ,
,
можно вычислить величину (6.11), которая вместе с (1.4) может быть подставлена в (1.14). Запишем выражение для 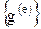 :
:
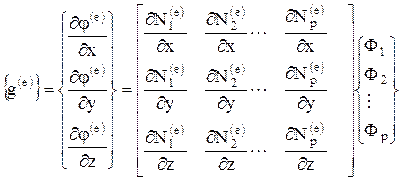 , (1.16)
, (1.16)
или
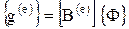 , (1.17) где [B] содержит информацию o производных от функций формы. Использование формул (1.4) и (1.17) позволяет записать интегралы по элементам в (1.14) в виде
, (1.17) где [B] содержит информацию o производных от функций формы. Использование формул (1.4) и (1.17) позволяет записать интегралы по элементам в (1.14) в виде
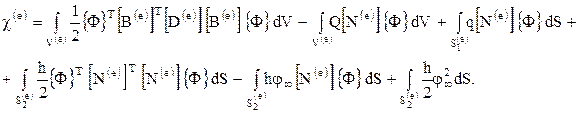 (1.18) Величины Q, q, j¥ и h - известные коэффициенты. Они внесены под знак интеграла, потому что могут изменяться внутри элемента. Дифференцирование (1.18) по {Ф} представляет собой простую операцию, если пользоваться правилами дифференцирования, приведенными в [33], и ее составляющие примут вид
(1.18) Величины Q, q, j¥ и h - известные коэффициенты. Они внесены под знак интеграла, потому что могут изменяться внутри элемента. Дифференцирование (1.18) по {Ф} представляет собой простую операцию, если пользоваться правилами дифференцирования, приведенными в [33], и ее составляющие примут вид
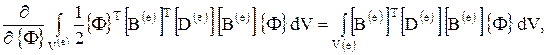
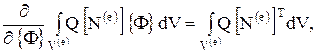
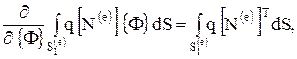
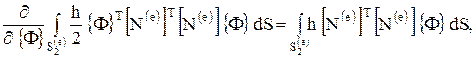
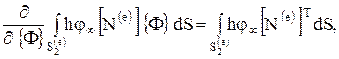
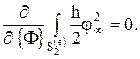
Вклад отдельного элемента 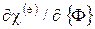 в общую сумму в
в общую сумму в 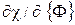 равен
равен
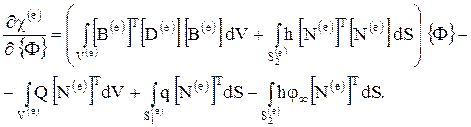
Эта совокупность интегралов может быть записана в компактной форме:
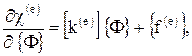 (1.19)
(1.19)
где
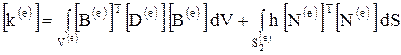
и
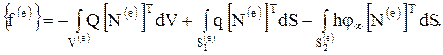
Окончательная система уравнений получается после подстановки выражения (1.19) в (1.15):

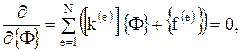 (1.20)
(1.20)
или
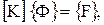
где 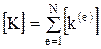 ,
,
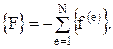 .
.
Затем из матриц элементов (1.20) составляется глобальная матрица относительно узлов элементов расчетной сети суммированием соответствующих матриц элементов, тем самым формируется глобальная система линейных алгебраических уравнений
[ U ]{Ф} = {F}, (1.21)
где [U] - ленточная матрица коэффициентов ums и m = 1, ..., q; s = 1, ..., q; q – число узлов триангуляционной (расчетной)сети; {Ф} - матрица-столбец узловых значений искомой функции Фm (векторного магнитного потенциала Аm), которые и подлежат определению; {F} - матрица-столбец свободных составляющих глобальной СЛАУ. Решается система уравнений (1.21) прямым или итерационным методом.
|
из
5.00
|
Обсуждение в статье: Уравнения метода конечных элементов. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

