Линейный гомополимер .

Примем n (l, x или s) в качестве переменной, характеризующей меру разброса степени полимеризации (распределения) в популяции, т.е. в образце полимера или пробе реакционной массы.

Если величина n дискретная переменная, то описывается частотной функцией

f_n = D F_n = F_n – F_{n - h}                   (8.1)

где h º D n – постоянный интервал между дискретными значениями n, а

 - функция распределения при дискретномn.

Если величина n непрерывная переменная, то описывается функцией плотности

                                                           (8.2)

где 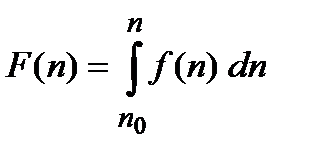 - функция распределения при непрерывном (n).

Распределение характеризуется формой, шириной и средней величиной n.

Так, приводится выражение для расчета среднего значения молекулярных масс любого порядка усреднения

                                                    (8.3)

где i – номер фракции, М _i – молекулярная масса i - той фракции, N_i – число макромолекул в i – той фракции.

При q= 1 получаем из (3) выражение для среднечисловой молекулярной массы

                                                        (8.4)

при q = 2 получаем выражение для среднемассовой молекулярной массы

                                                             (8.5)

 

а при q = 3 – выражение для z – средней молекулярной массы

                                     (8.6)

1/a

Зная параметр a из уравнения Марка-Хувинка([ h ] = kM ^a), нетрудно рассчитать и средневязкостную молекулярную массу:

 

(8.7)

 

 

Чем шире ММР, тем больше различаются между собой средние молекулярные массы, причем

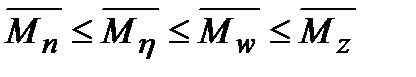                                                (8.8)

Показатель дисперсии (коэффициент полидисперсности) полимеров определяют как соотношение среднемассовой и среднечисловой молекулярных масс

                                                             (8.9)

При графическом изображении распределений различают три вида распределений: нормальное (рис. 1, кривая 1), Пуассона (кривая 2) и логарифмическое (кривая 3).

 

Рис. 8.1. Сравнение трёх распределений f_n с одним и тем же значением

1 – нормальное; 2 – Пуаcсона;      3 – логарифмическое

Различают моменты двух типов:

а) относительно начального значения распределения (n = 0); при этом статистический момент k-того порядка принимает выражения в случае n дискретной переменной

                                                       (8.10)

а в случае n непрерывной переменной

                                                 (8.11)

б) относительно среднего значения распределения (n = ), причём при дискретной переменной n статистический момент k – того порядка принимает вид

^

                                                                (8.12)

 

где                   - распределение, нормированное путём деления на размер популяции;

^

при непрерывной переменной n

 

                                                                      (8.13)

 

где                       - распределение, нормированное путём деления на размер популяции.

 

В выражениях (10) - (13) показатель k – целое число.

Для обозначения статистических моментов распределения концентраций примем f_n = c ( n ) – концентрация молекул произвольной длины n (число звеньев).

Тогда статистический момент порядка k распределения концентраций можно записать

при n дискретной

                                              (8.14)

при n непрерывной

                                           (8.15)

где Р( n ) – концентрация макромолекул длины n (функция молекулярно-числового распределения).

Практическое значение имеют первые четыре момента распределения:

 

 - момент нулевого порядка, равный концентрации мономер

 

ных звеньев;

                        - момент первого порядка, равный концентрации мономерных звеньев

- момент второго порядка;

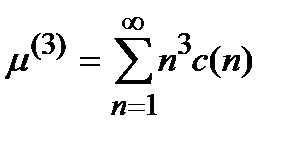
- момент третьего порядка.

 

Эти моменты позволяют через соотношения определять

среднечисловую степень полимеризации

                         (8.16)

среднемассовую степень полимеризации

                         (8.17)

Z-среднюю степень полимеризации

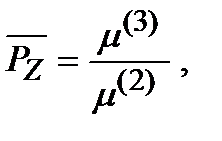                                  (8.18)

коэффициент полидисперсности, характеризующий ширину ММР

                                                       (8.19)

числовую функцию распределения полимера по молекулярным массам (числовое ММР)

                                                  (8.20)

массовую функцию распределения полимера по молекулярным массам (массовое ММР)

-                                                (8.21)

- доля всех мономерных звеньев, приходящихся на молекулы степени полимеризации l.

Любой статистический момент k-того порядка массового распределения можно определить по формуле

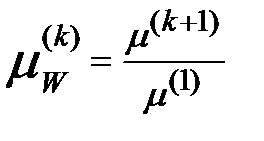                                                            (8.22)

Приведённая выше простая связь ММР с распределением концентраций с( l ) в реакционной системе справедлива только при проведении гомофазных процессов в однородных условиях. Если условия неоднородны (неравномерность перемешивания, градиент температур в зоне реакции), концентрации будут зависеть как от длины цепей ( l ), так и от координаты внутри реактора. Поэтому для расчёта ММР полимера, образующегося в неоднородных условиях, необходимо вычислить распределения концентраций компонентов произвольной степени полимеризации в различных точках реактора. Если полимер образуется в нескольких фазах одновременно (например, синтез новолачного фенолоформальдегидного полимера после расслоения реакционной системы на водную и олигомерную фазы), то ММР продуктов будет определяться концентрациями с( l ) в каждой из фаз.