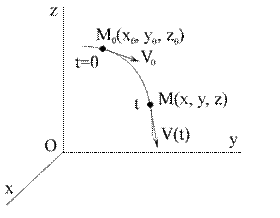|
Главная |
Вторая задача динамики
|
из
5.00
|
По заданной массе и действующей на точку силе можно определить уравнения движения этой точки.
Рассмотрим решение этой задачи в декартовой системе координат. В общем случае сила 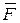 является функцией многих переменных. Проецируя (1.2) на декартовы оси, получим
является функцией многих переменных. Проецируя (1.2) на декартовы оси, получим
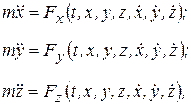 (1.5)
(1.5)
если рассматривать случай зависимости силы только времени, координат и скорости.
Законы движения материальной точки представляют собой систему трех линейных дифференциальных уравнений второго порядка относительно неизвестных функций х( t ), у( t ), z ( t ), где независимым параметром является время t .
Общий интеграл этих уравнений содержит шесть произвольных постоянных. Функции, удовлетворяющие дифференциальным уравнениям движения точки и содержащие шесть произвольных постоянных интегрирования, называются общим решением дифференциальных уравнений движения свободной точки и записываются в виде
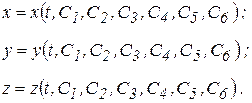
В каждой конкретной задаче постоянные интегрирования определяются из начальных условий задачи:
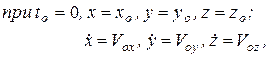 (1.6)
(1.6)
|
Рис. 1.5 |
где 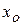 ,
, 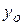 ,
, 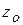 - координаты движущейся точки;
- координаты движущейся точки; 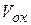 ,
, 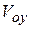 ,
,  - проекции ее скоростей (рис. 1.5).
- проекции ее скоростей (рис. 1.5).
Подчинив найденные первые и вторые интегралы дифференциальных уравнений (1.5) начальным условиям задачи (1.6), вычисляют все шесть постоянных интегрирования. Начальные условия задачи определяют единственное решение системы дифференциальных уравнений.
Интегрировать уравнения движения (1.5) можно с помощью определенных интегралов. Тогда нижние пределы интегрирования будут соответствовать значениям интегрируемых величин в начальный момент времени, т.е. начальным условиям задачи, верхние пределы интегрирования будут соответствоватьзначению интегрируемых величин при текущем времени t.
Основные виды прямолинейного движения точки
При прямолинейном движении скорость и ускорение точки все время направлены вдоль траектории точки. Совместим ось Ox с траекторией движущейся точки, тогда дифференциальное уравнение прямолинейного движения точки, согласно (1.5), имеет вид
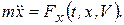 (1.5а)
(1.5а)
Начальные условия задачи задают в виде:
при 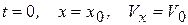 .
.
Наиболее простыми и интересными примерами прямолинейного движения материальной точки являются примеры, когда сила зависит от одного параметра.
Рассмотрим конкретные примеры на составление и интегрирование дифференциального уравнения (1.5а). Эти примеры позволят выявить некоторые особенности в решениях таких задач.
Постоянная сила
Пример 4. В результате полученного толчка тело весом mg начало скользить вниз с начальной скоростью 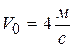 по шероховатой поверхности, расположенной под углом
по шероховатой поверхности, расположенной под углом 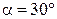 к горизонту (рис. 1.6). Определить путь, пройденный телом за время
к горизонту (рис. 1.6). Определить путь, пройденный телом за время 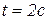 , если коэффициент трения скольжения тела по поверхности равен
, если коэффициент трения скольжения тела по поверхности равен 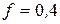 .
.
|
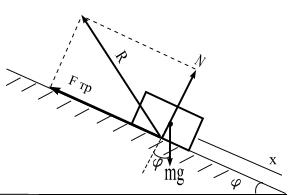
Рис. 1.6 |
Решение. Направим ось х вдоль наклонной поверхности (рис. 1.6). Совместим начало отсчета на оси х с положением тела в начальный момент времени.
Начальная скорость 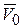 направлена вдоль оси х вниз, следовательно, начальные условия задачи имеют вид
направлена вдоль оси х вниз, следовательно, начальные условия задачи имеют вид
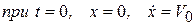 .
.
Тело не является свободным. Мысленно отбросим наклонную поверхность и заменим ее действие на тело реакцией 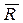 . Реакция шероховатой поверхности
. Реакция шероховатой поверхности 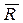 имеет две составляющие: нормальную
имеет две составляющие: нормальную 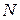 и силу трения
и силу трения 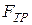 (
( 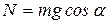 и направлена перпендикулярно поверхности, сила
и направлена перпендикулярно поверхности, сила 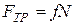 направлена в сторону, противоположную предполагаемому движению).
направлена в сторону, противоположную предполагаемому движению).
Запишем закон движения (1.5а):
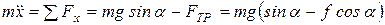 ;
;
и после сокращения на m , получим
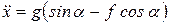 . (а)
. (а)
Согласно определению ускорения 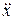 =
= 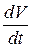 , тогда (а) запишем как
, тогда (а) запишем как
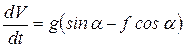 . (б)
. (б)
Получили линейное дифференциальное уравнение с неразделенными переменными. Для разделения переменных помножим правую и левую части уравнения (б) на dt,
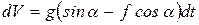 .
.
Проинтегрируем правую и левую части последнего уравнения с учетом заданных начальных условий ( 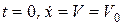 ). Нижние пределы интегрирования правой и левой части уравнения соответствуют значениям интегрируемых величин при t = 0, верхние пределы интегрирования – соответствуютзначениям интегрируемых величин при текущем времени t, т.е.
). Нижние пределы интегрирования правой и левой части уравнения соответствуют значениям интегрируемых величин при t = 0, верхние пределы интегрирования – соответствуютзначениям интегрируемых величин при текущем времени t, т.е.
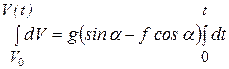 .
.
Вычислим интегралы
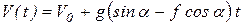 .
.
Для определения уравнения движения тела используем подстановку 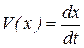 , получим
, получим
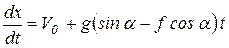 .
.
Разделяя переменные
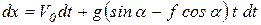 .
.
Проинтегрируем полученное уравнение с учетом заданных начальных условий (t = 0, x = 0):
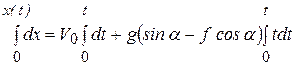 .
.
Вычисляя, получим
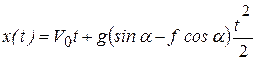 .
.
Подставив заданное значение 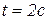 и
и  = 4
= 4 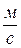 , получим путь, пройденный телом за 2с:
, получим путь, пройденный телом за 2с:
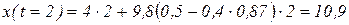 м.
м.
|
из
5.00
|
Обсуждение в статье: Вторая задача динамики |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы