 |
Главная |
Евклидово пространство
|
из
5.00
|
Определение. Линейное пространство R называется евклидовым, если имеется правило, которое позволяет для каждых двух векторов  построить действительное число, называемое скалярным произведением векторов
построить действительное число, называемое скалярным произведением векторов 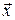 и
и  и обозначаемое (
и обозначаемое ( 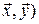 , причём это правило удовлетворяет следующим условиям:
, причём это правило удовлетворяет следующим условиям:

Если  -скалярный квадрат.
-скалярный квадрат.
Определение: Длиной вектора  в евклидовом пространстве называется квадратный корень из скалярного квадрата этого вектора, то есть
в евклидовом пространстве называется квадратный корень из скалярного квадрата этого вектора, то есть  .
.
Если  - любое действительное число, а
- любое действительное число, а  - любой вектор евклидова пространства, то
- любой вектор евклидова пространства, то  .
.
Определение: Вектор, длина которого равна 1, называется нормированным.
Если  - ненулевой вектор, то вектор
- ненулевой вектор, то вектор  - нормированный вектор или орт вектора
- нормированный вектор или орт вектора  .
.
Для любых векторов  и
и  в евклидовом пространстве выполняется неравенство Коши-Буняковского:
в евклидовом пространстве выполняется неравенство Коши-Буняковского:

Из неравенства Коши-Буняковского следует, что:
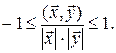
Угол  , определяемый равенством
, определяемый равенством 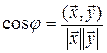 и принадлежащий
и принадлежащий  , называется углом между векторами
, называется углом между векторами  и
и  .
.
Если  и
и  - ненулевые векторы, а
- ненулевые векторы, а  , то
, то  . В этом случае говорят, что векторы
. В этом случае говорят, что векторы  и
и  ортогональны.
ортогональны.
Для произвольных векторов  и
и  евклидова пространства имеют место следующие важные соотношения:
евклидова пространства имеют место следующие важные соотношения:
1.  - неравенство треугольника.
- неравенство треугольника.
2. Пусть  - угол между векторами
- угол между векторами  и
и  , тогда
, тогда  (теорема косинусов).
(теорема косинусов).
Если 
 , то
, то  .
.
Ортогональный базис
Определение: Базис  евклидова пространства называется ортогональным, если
евклидова пространства называется ортогональным, если  при
при  .
.
Справедлива следующая теорема: во всяком евклидовом пространстве имеется ортогональный базис.
Если ортогональный базис состоит из нормированных вектор, то этот базис называется ортонормированным. Для ортонормированного базиса  выполняются равенства:
выполняются равенства:  .
.
Любой вектор  евклидова пространства, заданный в ортонормированном базисе, определяется равенством:
евклидова пространства, заданный в ортонормированном базисе, определяется равенством:
 .
.
Длина вектора  находится по формуле:
находится по формуле: 
Если  ,
,  , то
, то 
Два вектора  и
и  линейно зависимы (коллинеарны) тогда и только тогда, когда:
линейно зависимы (коллинеарны) тогда и только тогда, когда:  .
.
Условие ортогональности векторов  и
и  имеет вид:
имеет вид:
 .
.
Угол между двумя векторами  и
и  находится по формуле:
находится по формуле:
 .
.

Квадратичные формы
Определение: Квадратичной формой действительных переменных  называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени.
называется многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени.
Если n=2, то квадратичная форма имеет вид:
 .
.
Если количество переменных n=3, то:




В дальнейшем все необходимые формулировки и определения приведём к квадратичной форме 3-х переменных.
Матрица  , у которой
, у которой  называется матрицей квадратичной формы f(
называется матрицей квадратичной формы f(  ), а соответствующий определитель – определителем этой квадратичной формы. Так как А – симметрическая матрица (
), а соответствующий определитель – определителем этой квадратичной формы. Так как А – симметрическая матрица (  ), то корни
), то корни 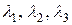 характеристического уравнения:
характеристического уравнения:

являются действительными числами.
Пусть

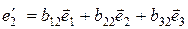

нормированные собственные векторы, соответствующие характеристическим числам  в ортонормированном базисе
в ортонормированном базисе  . В свою очередь векторы
. В свою очередь векторы  также образуют ортонормированный базис.
также образуют ортонормированный базис.
Матрица  является матрицей перехода от базиса
является матрицей перехода от базиса  к базису
к базису  .
.
Формулы выражения старых координат через новые при переходе к новому ортонормированному базису имеют вид:
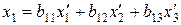

 .
.
Преобразовав с помощью этих формул квадратичную форму 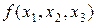 , получаем квадратичную форму
, получаем квадратичную форму  =
=  , не содержащую членов с произведениями
, не содержащую членов с произведениями 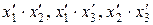 .
.
Принято говорить, что квадратичная форма  приведена к каноническому виду с помощью ортогонального преобразования В.
приведена к каноническому виду с помощью ортогонального преобразования В.
Пример:Привести к каноническому виду квадратичную форму 
В этом примере a 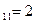 ,
,  ,
,  , характеристическое уравнение имеет вид:
, характеристическое уравнение имеет вид:  .
.  , имеем
, имеем  . Получаем следующие характеристические числа
. Получаем следующие характеристические числа  .
.
Для определения координат собственных векторов получаем системы линейных уравнений:
1) для 

 . Если
. Если  , где с - любое число, то
, где с - любое число, то  . Поэтому характеристическому числу
. Поэтому характеристическому числу  соответствует семейство собственных векторов
соответствует семейство собственных векторов  .
.
2) для 
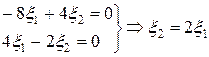 . Если
. Если  , где
, где  - любое число, то
- любое число, то  . Таким образом, характеристическому числу
. Таким образом, характеристическому числу  соответствует семейство собственных векторов
соответствует семейство собственных векторов 
Нормированные собственные векторы:


Матрица перехода к новому базису (матрица ортогонального преобразования) имеет вид:

Формулы преобразования координат:



Баранова Ирина Михайловна
ЛИНЕЙНАЯ АЛГЕБРА
Конспект лекций для студентов всех направлений подготовки бакалавров
Подписано в печать Формат 60х84 1/6
Объем 2 печ. л.
Тираж экз. Заказ №
ФГБОУ ВПО « Брянская государственная инженерно-технологическая академия»
Ред. – изд. отдел, тел. 64-95-62
Подразделение ОП
|
из
5.00
|
Обсуждение в статье: Евклидово пространство |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

