 |
Главная |
П.2 Матрица линейного преобразования
|
из
5.00
|
Пусть в n-мерном линейном пространстве R , базис которого  , задано линейное преобразование А. Так как
, задано линейное преобразование А. Так как  - векторы пространства R, то каждый из них можно разложить единственным способом по векторам базиса:
- векторы пространства R, то каждый из них можно разложить единственным способом по векторам базиса:
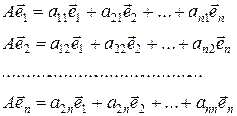
Определение: Матрица  называется матрицей линейного преобразования А в базисе
называется матрицей линейного преобразования А в базисе  . Столбцы этой матрицы составлены из коэффициентов в формулах преобразования базисных векторов. Линейное преобразование А, имеющее невырожденную матрицу преобразования А, называется невырожденным.
. Столбцы этой матрицы составлены из коэффициентов в формулах преобразования базисных векторов. Линейное преобразование А, имеющее невырожденную матрицу преобразования А, называется невырожденным.
Возьмём в пространстве R какой-нибудь вектор  . Так как
. Так как  , то и вектор
, то и вектор 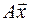 можно разложить по векторам базиса:
можно разложить по векторам базиса:
 =
= 
Координаты  вектора
вектора  выражаются через координаты
выражаются через координаты  вектора
вектора  по формулам:
по формулам:

Если  , то
, то  , а
, а  .
.
Замечание. Эти n равенств можно назвать линейным преобразованием А в базисе  . Коэффициенты в формулах этого линейного преобразования являются элементами строк матрицы А. Если линейным преобразованием Y = BX вектор
. Коэффициенты в формулах этого линейного преобразования являются элементами строк матрицы А. Если линейным преобразованием Y = BX вектор  переводится в Y, а преобразованием Z = AY вектор Y переводится в Z , то результат последовательного применения двух линейных преобразований B и А равносилен одному линейному преобразованию С с матрицей преобразования С=АВ; это преобразование переводит вектор Х в вектор Z.
переводится в Y, а преобразованием Z = AY вектор Y переводится в Z , то результат последовательного применения двух линейных преобразований B и А равносилен одному линейному преобразованию С с матрицей преобразования С=АВ; это преобразование переводит вектор Х в вектор Z.
Пример. В 4  -мерном линейном пространстве рассматривается линейное преобразование А. Записать это преобразование в координатной форме, если:
-мерном линейном пространстве рассматривается линейное преобразование А. Записать это преобразование в координатной форме, если:
 ,
,  ,
,  ,
,  .
.
Матрица преобразования имеет вид:
 , следовательно, преобразование А в координатной форме записывается так:
, следовательно, преобразование А в координатной форме записывается так:  ,
,  ,
,  ,
,  .
.
П.3 Характеристические числа и собственные векторы линейного
преобразования
Пусть R – заданное n-мерное линейное пространство.
Определение: Ненулевой вектор  называется собственным вектором линейного преобразования А, если найдётся такое число
называется собственным вектором линейного преобразования А, если найдётся такое число  , что выполняется равенство
, что выполняется равенство  . Само число
. Само число  называется характеристическим числом линейного преобразования А, соответствующим вектору
называется характеристическим числом линейного преобразования А, соответствующим вектору  .
.
Если линейное преобразование А в базисе  имеет матрицу
имеет матрицу
 , то характеристическими числами линейного преобразования А служат действительные корни
, то характеристическими числами линейного преобразования А служат действительные корни  уравнения n-степени, которое можно записать:
уравнения n-степени, которое можно записать:

Это уравнение называется характеристическим уравнением, а его левая часть – характеристическим многочленом линейного преобразования А. Собственным вектором  , соответствующим характеристическому числу
, соответствующим характеристическому числу  , является любой вектор
, является любой вектор  , координаты которого удовлетворяют системе линейных однородных уравнений:
, координаты которого удовлетворяют системе линейных однородных уравнений:

Пример. Найти характеристические числа и собственные векторы линейного преобразования А, определяемого уравнениями:

Матрица преобразования:  , характеристическое уравнение имеет вид
, характеристическое уравнение имеет вид
 ,
, 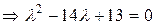
Характеристические числа 
Для определения координат собственных векторов получаем системы линейных уравнений:
1) для 

 . Если
. Если  , где
, где  - любое число, то
- любое число, то  . Поэтому характеристическому числу
. Поэтому характеристическому числу  соответствует семейство собственных векторов
соответствует семейство собственных векторов  .
.
2) для 

 . Если
. Если  , где
, где  - любое число, то
- любое число, то  . Таким образом, характеристическому числу
. Таким образом, характеристическому числу  соответствует семейство собственных векторов
соответствует семейство собственных векторов 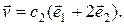
|
из
5.00
|
Обсуждение в статье: П.2 Матрица линейного преобразования |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

