Метод наименьших квадратов и его применения.

Задача приближения функции возникает при решении многих задач, а иногда и как самостоятельная. Например, если известна некоторая функция, которая задана аналитически или таблично, но получение значений этой функции сопряжено с большим объемом вычислений, то можно поставить задачу приближения этой функции другой функцией, близкой к исходной, но более удобной для расчетов. Например, замена функции многочленом позволяет получать простые формулы численного дифференцирования и интегрирования. Возникает также и другая задача – восстановление аналитического вида функции на некотором отрезке по заданным на нём значениям функции в дискретном множестве точек. Замена таблицы приближающей функцией позволяет получать ее значения в промежуточных точках. Теория приближения функций является важным вспомогательным аппаратом при численном решении дифференциальных уравнений.

В общем случае при постановке задачи приближения необходимо решить следующие вопросы.

Во-первых, требуется определить, какой класс приближающих функций необходимо выбрать. Здесь все зависит от вида приближаемой функции и целей, для которых в дальнейшем будет использоваться приближающая функция. Широко используются следующие классы функций: многочлены, тригонометрические функции, показательные и логарифмические функции и др.

Во-вторых, необходимо выбрать критерий близости исходной и приближающей функций. В качестве критерия можно выбрать, например, точное совпадение приближаемой и приближающей функций – задача интерполирования. Но при большом количестве узлов он является неудобным и сложным, так как потребует нахождения либо многочлена большой степени, либо другой громоздкой функции с графиком, проходящим через все табличные точки.

Часто с помощью какой-либо простой функции с проходящим около табличных точек графиком удается добиться эффекта сглаживания ошибок и получить достаточно точное приближение. В общем случае, необходимо добиться того, чтобы отклонение приближающей функции от приближаемой в табличных точках было минимально

Но использовать в качестве критерия близости сумму отклонений не имеет смысла, т. к. при сложении разности будут компенсировать друг друга. Поэтому, учитывая также и то, что величина погрешности в экспериментальных точках может быть разной, необходимо минимизировать среднее значение суммы абсолютных погрешностей в заданных точках. Если приближаемая функция y = f(x) задана таблицей своих значений: y_j  = f(x_j), j = 1, 2, ..., n, и имеется некоторая приближающая функция Ф(х), определенная для всех значений x_j, то данный критерий запишется следующим образом:

Это условие было предложено Эджвортом. В современной литературе этот способ аппроксимации носит название равномерное приближение. Однако приближение функций по этому способу в широкое употребление не вошло.

Вместо среднего значения модуля отклонения используется среднее квадратическое отклонение эмпирической и теоретической величины в соответствии с выражением:

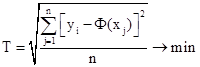
Если же приближаемая функция y = f (x) задана аналитически, т. е. она считается известной в любой точке x отрезка [a; b], то близость между y и приближающей функцией Ф(x) понимается в интегральном смысле:

Такой выбор критерия близости и используется в методе наименьших квадратов.

Метод наименьших квадратов был предложен в начале XIX столетия К. Гауссом (1794–95) и независимо от него А. Лежандром (1805–06). Первоначально этот метод использовался для обработки результатов астрономических и геодезических наблюдений. Строгое математическое обоснование и установление границ содержательной применимости метода наименьших квадратов были даны А. А. Марковым и А. Н. Колмогоровым. Сейчас этот метод представляет собой один из важнейших разделов математической статистики и широко используется для статистических выводов в различных областях науки и техники.

Сущность обоснования метода наименьших квадратов (по Гауссу) заключается в допущении, что «убыток» от замены точного (неизвестного) значения физической величины её приближённым значением X, вычисленным по результатам наблюдений, пропорционален квадрату ошибки:

(X – μ)², где μ – оцениваемая величина.

В этих условиях оптимальной оценкой естественно признать такую лишённую систематической ошибки величину X, для которой среднее значение "убытка" минимально. Именно это требование и составляет основу метода наименьших квадратов.

Рассмотрим частный случай зависимости наблюдаемой величины  от искомых параметров :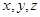

.

В дискретных значениях аргумента  получим n значений , где  - ошибка измерения величины l в момент .

Обозначим:

 .

Теперь для определения искомых x, y, z будем иметь систему n уравнений:

                                 .

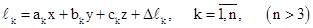Критерий  будет выглядеть следующим образом:

                                 .

Построим систему нормальных уравнений:

,

                                          ,

                                          .

Выполнив дифференцирование, получим

                                          ,

                                          ,

                                          .

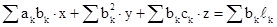Имеем систему, состоящую из трех линейных уравнений с тремя неизвестными, которую легко тем или иным способом решить.

       Для обозначения сумм произведений или квадратов Гаусс предложил применять прямые скобки следующим образом

, и т.д.

В этих обозначениях нормальные уравнения примут вид

,

,

.

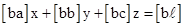Основное свойство нормальных уравнений - симметричность матрицы системы:

Решить эту систему можно используя, например, формулы Крамера, или один из матричных способов.

Покажем численный пример применения МНК для аппроксимации результатов эксперимента линейным уравнением первой степени.

В результате эксперимента получены семь значений искомой функции Y при семи значениях аргумента X. Используя метод наименьших квадратов, найти функциональную зависимость между Х и У в виде линейной функции у = ах + b. Построить график этой функции. Отметить экспериментальные значения.

 Решение: Построим корреляционное поле по данным семи наблюдений.

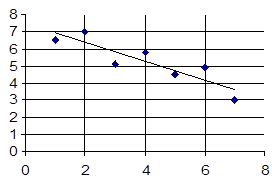Получили точки определяющие линию регрессии У на Х. Характер изменения функции У позволяет предположить, что зависимость между У и Х близка к линейной вида у = ах + b.

Коэффициенты "a и b" уравнения найдём, выполнив необходимые вычисления:

Расчеты сведем в таблицу. В правом столбце этой таблицы записаны суммы по её строкам.

Номер измерения	1	2	3	4	5	6	7	Сумма
Х	1	2	3	4	5	6	7	28
У	6,5	7,0	5,1	5,8	4,5	4,9	3,0	36,8
х2	1	4	9	16	25	36	49	140
х∙y	6,5	14	15,3	23,2	22,5	29,4	21	131,9
	6,90	6,35	5,80	5,26	4,71	4,16	3,62	36,80
	1,54	3,04	0,02	0,29	0,57	0,13	5,09	10,70
	0,16	0,42	0,50	0,29	0,04	0,54	0,38	2,34

Нормальные уравнения для этого случая будут иметь вид:

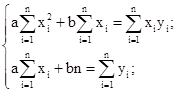
Из этих уравнений имеем:

Т.о. линейная зависимость У от Х имеет вид: .

По этому уравнению вычислены теоретические значения величины .

Прямая линия зависимости У от Х построена вместе с ломаной линией по двум точкам:

При х = 1.      у = 7,443 – 0,5464·1 = 6,897.

При х = 7.  у = 7,443 – 0,5464·7 = 3,618.

Определив сумму квадратов отклонений измеренной величины "у" от её средних значений и сумму квадратов отклонений этой величины от её значений, полученных по уравнению регрессии , можно оценить качество полученного уравнения по коэффициенту детерминации:

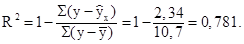
Это означает, что зависимость переменной "у" от переменной "х" определяется полученным уравнением регрессии на 78,1%, а вариация величины "у" на оставшиеся 21,9% объясняется другими факторами.