П2.2.2. Методы сглаживания временного ряда (выделение неслучайной составляющей)

Методы выделения неслучайной составляющей в траектории, отражающей поведение временного ряда, подразделяются на два типа.

Методы первого типа (аналитические) основаны на допущении, что известен общий вид неслучайной составляющей в разложении (1.1.1)

f(t) = c₁f_тр(t) + c₂j(t) +c₃y(t).                           (П2.8)

Например, если известно, что неслучайная составляющая временного ряда описывается линейной функцией времени f(t) = q₀ + q₁t, где q₀ и q₁ - некоторые неизвестные параметры модели, то задача ее выделения (задача элиминирования случайных остатков или задача сглаживания временного ряда) сводится к задаче построения хороших оценок  и  для параметров модели.

Методы второго типа (алгоритмические) не связаны ограничительным допущением о том, что общий аналитический вид искомой функции (П2.8) известен исследователю. В этом смысле они являются более гибкими, более привлекательными. Однако «на выходе» задачи они предлагают исследователю лишь алгоритм расчета оценки  для искомой функции f(t) в любой наперед заданной точке t и не претендуют на аналитическое представление функции (П2.8).

Аналитические методы выделения (оценки) неслучайной составляющей временного ряда. Эти методы реализуются в рамках моделей регрессии, в которых в роли зависимой переменной выступает переменная x_t, а в роли единственной объясняющей переменной - время t. Таким образом, рассматривается модель регрессии вида

x_t = f(t, q) + e _t, t = 1,…, T,

в которой общий вид функции f(t, q) известен, но неизвестны значения параметров q = (q₀, q₁,…, q _m). Оценки параметров  строятся по наблюдениям . Выбор метода оценивания зависит от гипотетического вида функции f(t, q) и стохастической природы случайных регрессионных остатков e _t.

Алгоритмические методы выделения неслучайной составляющей временного ряда (методы скользящего среднего). В основе этих методов элиминирования случайных флуктуаций в поведении анализируемого временного ряда лежит простая идея: если «индивидуальный» разброс значений члена временного ряда x_t около своего среднего (сглаженного) значения a характеризуется дисперсией s², то разброс среднего из N членов временного ряда (x₁ + x₂ +…+ x_T) / N около того же значения a будет характеризоваться гораздо меньшей величиной дисперсии, а именно дисперсией, равной s² / N. А уменьшение меры случайного разброса (дисперсии) и означает как раз сглаживание соответствующей траектории. Поэтому выбирают некоторую нечетную «длину усреднения» N = 2m + 1, измеренную в числе подряд идущих членов анализируемого временного ряда. А затем сглаженное значение   временного ряда x_t вычисляют по значениям x_{t - m}, x_{t - m+1},…, x_t, x_t+1,…, x_t+m по формуле

                          (П2.9)

где w_k (k = -m, - m + 1,…, m) - некоторые положительные «весовые» коэффициенты, в сумме равные единице, т.е. w_k > 0 и . Поскольку, изменяя t от m + 1 до T - m, мы как бы «скользим» по оси времени, то и методы, основанные на формуле (П2.9), принято называть методами скользящей средней (МСС).

Очевидно, один МСС отличается от другого выбором параметров m и w_k.

Определение параметров w_k основано на следующей процедуре. В соответствии с теоремой Вейерштрасса любая гладкая функция f(x) при самых общих допущениях может быть локально представлена алгебраическим полиномом подходящей степени p. Поэтому берем первые 2m + 1 членов временного ряда x₁,…, x_2m+1, строим с помощью МНК полином 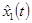 степени p, аппроксимирующий поведение этой начальной части траектории временного ряда, и используем этот полином для определения оценки  сглаженного значения f(t) временного ряда в средней (т.е. (m + 1)-й) точке этого отрезка ряда, т.е. полагаем 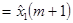. Затем «скользим» по оси времени на один такт и таким же способом подбираем полином  той же степени p к отрезку временного ряда x₂,…, x_m+2 и определяем оценку сглаженного значения временного ряда в средней точке сдвинутого на единицу отрезка временного ряда, т.е. 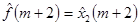, и т.д.

В результате мы найдем оценки для сглаженных значений  анализируемого временного ряда при всех t, кроме t = 1,…, m и t = T,… T - m + 1.

Подбор наилучшего (в смысле критерия МНК) аппроксимирующего полинома к траектории анализируемого временного ряда приводит к формуле вида (П2.9), причем результат не зависит от того, для какого именно из «скользящих» временных интервалов был осуществлен этот подбор.

Метод экспоненциально взвешенного скользящего среднего (метод Брауна [ Brown (1963)]). В соответствии с этим методом оценка сглаженного значения 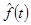 в точке t определяется как решение оптимизационной задачи вида

                              (П2.10)

где 0 < l < 1. Следовательно, веса l ^k в критерии Q(f) обобщенного («взвешенного») МНК уменьшаются экспоненциально по мере удаления наблюдений x_{t - k} в прошлое.

Решение оптимизационной задачи (П2.10) дает:

                       (П2.11)

В отличие от обычного МСС здесь скользит только правый конец интервала усреднения и, кроме того, веса экспоненциально уменьшаются по мере удаления в прошлое. Формула (П2.11) дает оценку сглаженного значения временного ряда не в средней, а в правой конечной точке интервала усреднения.