 |
Главная |
П2.2.3. Подбор порядка аппроксимирующего полинома с помощью метода последовательных разностей
|
из
5.00
|
Реализация алгоритмических методов выделения неслучайной составляющей временного ряда связана с необходимостью подбора порядка p локально-аппроксимирующего полинома. Эта же задача возникает и при реализации аналитических методов выделения неслучайной составляющей. При решении этой задачи широко используется так называемый метод последовательных разностей членов анализируемого временного ряда, который основан на следующем математическом факте: если анализируемый временной ряд xt содержит в качестве своей неслучайной составляющей алгебраический полином f(t) = q0 + q1t + q p tp порядка p, то переход к последовательным разностям порядка p + 1, исключает неслучайную составляющую, оставляя элементы, выражающиеся только через остаточную случайную компоненту e t.
Обсудим способ подбора порядка p полинома, представляющего собой неслучайную составляющую f(t) в разложении анализируемого временного ряда xt. Заметим, прежде всего, что если мы знаем, что среднее значение наблюдаемой случайной величины x равно нулю (Ex = 0), то выборочным аналогом ее дисперсии является величина  , где x I, i = 1, 2,…, T - наблюденные значения этой случайной величины. Если же Ex ¹ 0, то выборочным аналогом дисперсии будет статистика
, где x I, i = 1, 2,…, T - наблюденные значения этой случайной величины. Если же Ex ¹ 0, то выборочным аналогом дисперсии будет статистика  , так что величина
, так что величина  будет давать в этом случае существенно завышенные оценки для Dx. Возвращаясь к последовательному переходу к разностям Dk xt, k = 1, 2,…, p + 1, отметим, что при всех k < p + 1 средние значения этих разностей будут отличны от нуля, так как будут выражаться не только через остатки e t, но и через коэффициенты q0, q1,…, q p и степени t. И только для k ³ p + 1 можно утверждать, что:
будет давать в этом случае существенно завышенные оценки для Dx. Возвращаясь к последовательному переходу к разностям Dk xt, k = 1, 2,…, p + 1, отметим, что при всех k < p + 1 средние значения этих разностей будут отличны от нуля, так как будут выражаться не только через остатки e t, но и через коэффициенты q0, q1,…, q p и степени t. И только для k ³ p + 1 можно утверждать, что:
E(Dk xt) = 0 и  .
.
С учетом этих замечаний можно сформулировать следующее правило подбора порядка сглаживающего полинома p, называемое методом последовательных разностей.
Последовательно для k = 1, 2,… вычисляем разности Dk xt (t = 1,…, T - k), а также величины
 (П2.12)
(П2.12)
Анализируем поведение величины  в зависимости от k. Величина
в зависимости от k. Величина  как функция k будет демонстрировать явную тенденцию к убыванию до тех пор, пока k не достигнет величины p + 1. Начиная с этого момента величина (П2.12) стабилизируется, оставаясь (при дальнейшем увеличении p) приблизительно на одном уровне. Поэтому значение k = k0, начиная с которого величина
как функция k будет демонстрировать явную тенденцию к убыванию до тех пор, пока k не достигнет величины p + 1. Начиная с этого момента величина (П2.12) стабилизируется, оставаясь (при дальнейшем увеличении p) приблизительно на одном уровне. Поэтому значение k = k0, начиная с которого величина  стабилизируется, и будет давать завышенный на единицу искомый порядок сглаживающего полинома, т.е. p = k0 - 1.
стабилизируется, и будет давать завышенный на единицу искомый порядок сглаживающего полинома, т.е. p = k0 - 1.
Этот метод привлекателен своей простотой, но его практическое применение требует определенной осторожности. Последовательные значения  не являются независимыми, и часто обнаруживается тенденция их медленного убывания (а иногда возрастания) без видимой сходимости к постоянному значению. Кроме того, процесс перехода к разностям имеет тенденцию уменьшать относительное значение любого систематического движения, кроме сезонных эффектов с периодом, близким к временному интервалу, так что сходимость отношения
не являются независимыми, и часто обнаруживается тенденция их медленного убывания (а иногда возрастания) без видимой сходимости к постоянному значению. Кроме того, процесс перехода к разностям имеет тенденцию уменьшать относительное значение любого систематического движения, кроме сезонных эффектов с периодом, близким к временному интервалу, так что сходимость отношения  не доказывает, что ряд первоначально состоял из полинома плюс случайный остаток, а только то, что он может быть приближенно представлен таким образом. Однако для нас этот метод ценен лишь тем, что он дает верхний предел порядка полинома p, который целесообразно использовать для элиминирования неслучайной составляющей.
не доказывает, что ряд первоначально состоял из полинома плюс случайный остаток, а только то, что он может быть приближенно представлен таким образом. Однако для нас этот метод ценен лишь тем, что он дает верхний предел порядка полинома p, который целесообразно использовать для элиминирования неслучайной составляющей.
П2.3. Модели стационарных временных рядов и их идентификация. Модели авторегрессии порядка p (AR(p)-модели)
В П2.2 рассматривался класс стационарных временных рядов, в рамках которого подбирается модель, пригодная для описания поведения случайных остатков исследуемого временного ряда (1.1.1). Здесь рассматривается набор линейных параметрических моделей из этого класса и методы их идентификации. Таким образом, речь здесь идет не о моделировании временных рядов, а о моделировании их случайных остатков e t, получающихся после элиминирования из исходного временного ряда xt его неслучайной составляющей (П2.8). Следовательно, в отличие от прогноза, основанного на регрессионной модели, игнорирующего значения случайных остатков, в прогнозе временных рядов существенно используется взаимозависимость и прогноз самих случайных остатков.
Введем обозначения. Так как здесь описывается поведение случайных остатков, то моделируемый временной ряд обозначим e t, и будем полагать, что при всех t его математическое ожидание равно нулю, т.е. Ee t, º 0. Временные последовательности, образующие «белый шум», обозначим d t.
Описание и анализ, рассматриваемых ниже моделей, формулируется в терминах общего линейного процесса, представимого в виде взвешенной суммы настоящего и прошлых значений белого шума, а именно:
 (П2.13)
(П2.13)
где b0 = 1 и 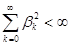 .
.
Таким образом, белый шум представляет собой серию импульсов, в широком классе реальных ситуаций генерирующих случайные остатки исследуемого временного ряда.
Временной ряд e t можно представить в эквивалентном (П2.13) виде, при котором он получается в виде классической линейной модели множественной регрессии, в которой в качестве объясняющих переменных выступают его собственные значения во все прошлые моменты времени:
 (П2.14)
(П2.14)
При этом весовые коэффициенты p1, p2,… связаны определенными условиями, обеспечивающими стационарность ряда e t. Переход от (П2.14) к (П2.13) осуществляется с помощью последовательной подстановки в правую часть (П2.14) вместо e t -1, e t -2,… их выражений, вычисленных в соответствии с (П2.14) для моментов времени t - 1, t - 2 и т.д.
Рассмотрим также процесс смешанного типа, в котором присутствуют как авторегрессионные члены самого процесса, так и скользящее суммирование элементов белого шума:

Будем подразумевать, что p и q могут принимать и бесконечные значения, а также то, что в частных случаях некоторые (или даже все) коэффициенты p или b равны нулю.
Рассмотрим сначала простейшие частные случаи.
Модель авторегрессии 1-го порядка - AR(1) (марковский процесс). Эта модель представляет собой простейший вариант авторегрессионного процесса типа (П2.14), когда все коэффициенты кроме первого равны нулю. Соответственно, она может быть определена выражением
e t = a e t -1 + d t, (П2.15)
где a - некоторый числовой коэффициент, не превосходящий по абсолютной величине единицу (|a| < 1), а d t - последовательность случайных величин, образующая белый шум. При этом e t зависит от d t и всех предшествующих d, но не зависит от будущих значений d. Соответственно, в уравнении (П2.15) d t не зависит от e t -1 и более ранних значений e . В связи с этим, d t называют инновацией (обновлением).
Последовательности e, удовлетворяющие соотношению (П2.15), часто называют также марковскими процессами. Это означает, что
Ee t º 0, (П2.16)
r(e t, e t±k) = a k, (П2.17)
De t =  , (П2.18)
, (П2.18)
cov(e t, e t±k) = a kDe t. (П2.19)
Одно важное следствие (П2.19) состоит в том, что если величина |a| близка к единице, то дисперсия e t будет намного больше дисперсии d. А это значит, что если соседние значения ряда e t сильно коррелированы, то ряд довольно слабых возмущений d t будет порождать размашистые колебания остатков e t.
Основные характеристики процесса авторегрессии 1-го порядка следующие.
Условие стационарности ряда (П2.15) определяется требованием к коэффициенту a: |a| < 1,
или, что то же, корень z0 уравнения 1 - a z = 0 должен быть по абсолютной величине больше единицы.
Автокорреляционная функция марковского процесса определяется соотношением (П2.17):
r(t) = r(e t, e t±t) = a t. (П2.20)
Отсюда же, в частности, следует простая вероятностная интерпретация параметра a: a = r(e t, e t±1),
т.е. значение a определяет величину корреляции между двумя соседними членами ряда e t.
Из (П2.20) видно, что степень тесноты корреляционной связи между членами последовательности (П2.15) экспоненциально убывает по мере их взаимного удаления друг от друга во времени.
Частная автокорреляционная функция rчаст(t) = r(e t, e t+t | e t+1 = e t+2=…= e t+t-1 = 0) может быть подсчитана с помощью формул (П2.4)–(П2.5). Непосредственное вычисление по этим формулам дает следующий простой результат: значения частной корреляционной функции rчаст(t) равны нулю для всех t = 2, 3,…. Это свойство может быть использовано при подборе модели: если вычисленные выборочные частные корреляции  статистически незначимо отличаются от нуля при t = 2, 3,…, то использование модели авторегрессии 1-го порядка для описания поведения случайных остатков временного ряда не противоречит исходным статистическим данным.
статистически незначимо отличаются от нуля при t = 2, 3,…, то использование модели авторегрессии 1-го порядка для описания поведения случайных остатков временного ряда не противоречит исходным статистическим данным.
Спектральная плотность 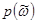 марковского процесса (П2.15) может быть подсчитана с учетом известного вида автокорреляционной функции (П2.20):
марковского процесса (П2.15) может быть подсчитана с учетом известного вида автокорреляционной функции (П2.20):

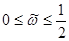
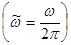 .
.
В случае значения параметра a близкого к 1, соседние значения ряда e t близки друг к другу по величине, автокорреляционная функция экспоненциально убывает оставаясь положительной, а в спектре преобладают низкие частоты, что означает достаточно большое среднее расстояние между пиками ряда e t. При значении параметра a близком к –1, ряд быстро осциллирует (в спектре преобладают высокие частоты), а график автокорреляционной функции экспоненциально спадает до нуля с попеременным изменением знака.
Идентификация модели, т.е. статистическое оценивание ее параметров a и  по имеющейся реализации временного ряда xt (а не его остатков, которые являются ненаблюдаемыми), основана на соотношениях (П2.16)-(П2.19) и может быть осуществлена с помощью метода моментов. Для этого следует предварительно решить задачу выделения неслучайной составляющей
по имеющейся реализации временного ряда xt (а не его остатков, которые являются ненаблюдаемыми), основана на соотношениях (П2.16)-(П2.19) и может быть осуществлена с помощью метода моментов. Для этого следует предварительно решить задачу выделения неслучайной составляющей  , что позволит оперировать в дальнейшем остатками
, что позволит оперировать в дальнейшем остатками
 (П2.21)
(П2.21)
Затем подсчитывается выборочная дисперсия 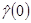 остатков по формуле
остатков по формуле
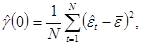
где 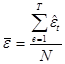 , а «невязки» (остатки) вычислены по формуле (П2.21).
, а «невязки» (остатки) вычислены по формуле (П2.21).
Оценку  параметра a получаем с помощью формулы (П2.18), подставляя в нее вместо коэффициента корреляции его выборочное значение, т.е.
параметра a получаем с помощью формулы (П2.18), подставляя в нее вместо коэффициента корреляции его выборочное значение, т.е.  .
.
Наконец, оценка  параметра
параметра  основана на соотношении (П2.19), в котором величины De t и a заменяются оценками, соответственно,
основана на соотношении (П2.19), в котором величины De t и a заменяются оценками, соответственно,  и
и  :
: 
Модели авторегрессии 2-го порядка – AR (2) (процессы Юла). Эта модель, как и AR(1), представляет собой частный случай авторегрессионного процесса, когда все коэффициенты p j в правой части (П2.14) кроме первых двух, равны нулю. Соответственно, она может быть определена выражением
e t = a1e t-1+ a2e t-2+ d t, (П2.22)
где последовательность d1, d2,… образует белый шум.
Условия стационарности ряда (П2.22) (необходимые и достаточные) определяются как: 
В рамках общей теории моделей те же самые условия стационарности получаются из требования, чтобы все корни соответствующего характеристического уравнения лежали бы вне единичного круга. Характеристическое уравнение для модели авторегрессии 2-го порядка имеет вид: 
Автокорреляционная функция процесса Юла подсчитывается следующим образом. Два первых значения r(1) и r(2) определены соотношениями

а значения для r(t), t = 3, 4,… вычисляются с помощью рекуррентного соотношения r(t) = a1r(t - 1) + a2r(t - 2).
Частная автокорреляционная функция временного ряда, сгенерированного моделью авторегрессии 2-го порядка, обладает следующим отличительным свойством: r част(t) = 0 при всех t = 3, 4,…
Спектральная плотность  процесса Юла может быть вычислена с помощью формулы:
процесса Юла может быть вычислена с помощью формулы: 
Идентификация модели авторегрессии 2-го порядка основана на соотношениях, связывающих между собой неизвестные параметры модели a1, a2 и  со значениями различных моментов «наблюдаемого» временного ряда e t.
со значениями различных моментов «наблюдаемого» временного ряда e t.
По значениям  вычисляются оценки
вычисляются оценки  и
и  , соответственно, дисперсии De t и автокорреляций r(1) и r(2). Это делается с помощью соотношений (П2.2) и (П2.3):
, соответственно, дисперсии De t и автокорреляций r(1) и r(2). Это делается с помощью соотношений (П2.2) и (П2.3):

После этого можно получить оценки 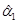 и
и  из соотношений
из соотношений

Наконец, оценку параметра  получаем с помощью
получаем с помощью

Модели авторегрессии p - го порядка – AR ( p ) ( p ³ 3). Эти модели, образуя подмножество в классе общих линейных моделей, сами составляют достаточно широкий класс моделей. Если в общей линейной модели (П2.14) полагать все параметры p j, кроме первых p коэффициентов, равными нулю, то мы приходим к определению AR(p)-модели:
 (П2.23)
(П2.23)
где последовательность случайных величин d1, d2,… образует белый шум.
Условия стационарности процесса, генерируемого моделью (П2.23), также формулируются в терминах корней его характеристического уравнения
1 - a1z - a2z2-…- a p zp = 0.
Для стационарности процесса необходимо и достаточно, чтобы все корни характеристического уравнения лежали бы вне единичного круга, т.е. превосходили бы по модулю единицу.
Автокорреляционная функция процесса (П2.23) может быть вычислена с помощью рекуррентного соотношения по первым p ее значениям r(1),…, r(p). Это соотношение имеет вид:
r (t) = a1r(t - 1) + a2r(t - 2) +…+ a p r(t - p), t = p + 1, p + 2,... (П2.24)
Частная автокорреляционная функция процесса (П2.23) будет иметь ненулевые значения лишь при t £ p; все значения rчаст(p) при t > p будут нулевыми. Это свойство частной автокорреляционной функции AR(p)-процесса используется, в частности, при подборе порядка в модели авторегрессии для конкретных анализируемых временных рядов. Если, например, все частные коэффициенты автокорреляции, начиная с порядка k, статистически незначимо отличаются от нуля, то порядок модели авторегрессии естественно определить равным p = k - 1.
Спектральная плотность процесса авторегрессии p -го порядка определяется с помощью формулы:

Идентификация модели авторегрессии p -го порядка основана на соотношениях, связывающих между собой неизвестные параметры модели и автокорреляции исследуемого временного ряда. Для вывода этих соотношений последовательно подставляются в (П2.24) значения t = 1, 2,…, p. Получается система линейных уравнений относительно a1, a2,…, a p:
 (П2.25)
(П2.25)
называемая уравнениями Юла–Уокера [Yule (1927)], [Walker (1931)]. Оценки  для параметров a k получим, заменив теоретические значения автокорреляций r(k) их оценками
для параметров a k получим, заменив теоретические значения автокорреляций r(k) их оценками  и решив полученную таким образом систему уравнений. Оценка параметра
и решив полученную таким образом систему уравнений. Оценка параметра  получается из соотношения
получается из соотношения  заменой всех участвующих в правой части величин их оценками.
заменой всех участвующих в правой части величин их оценками.
Заключение
Разнообразные содержательные задачи экономического анализа требуют использования статистических данных, характеризующих исследуемые экономические процессы и развернутых во времени в форме временных рядов. При этом одни и те же временные ряды используются для решения разных содержательных проблем.
Литература
1. Айвазян С.А., Мхитарян В.С. (1998) Прикладная статистика и основы эконометрии. – М.: ЮНИТИ, 1998.
2. Бокс Дж., Дженкинс Г. (1974) Анализ временных рядов. Прогноз и управление. - М.: Мир, 1974. - Вып. 1, 2.
3. Большев Л.Н., Смирнов Н.В. (1965) Таблицы математической статистики. - М.: Наука, 1965.
4. Дженкинс Г., Ватс Д. (1971, 1972) Спектральный анализ и его применения. - М.: Мир, 1971, 1972. - Вып. 1,2.
5. Джонстон Дж. (1980) Эконометрические методы. - М.: Статистика, 1980.
|
из
5.00
|
Обсуждение в статье: П2.2.3. Подбор порядка аппроксимирующего полинома с помощью метода последовательных разностей |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

