Показатели рядов динамики

При изучении явления во времени перед исследователем встает проблема описания интенсивности изменения и расчета средних показателей динамики. Решается она путем построения соответствующих показателей.

Для характеристики интенсивности изменения во времени такими показателями будут:

1) абсолютный прирост,
2) темпы роста,
3) темпы прироста,
4) абсолютное значение одного процента прироста.

Расчет показателей динамики представлен в следующей таблице.

Таблица 1

Показатель	Базисный	Цепной
Абсолютный прирост *	Yi-Y0	Yi-Yi-1
Коэффициент роста (Кр)	Yi : Y0	Yi : Yi-1
Темп роста (Тр)	(Yi : Y0)×100	(Yi : Yi-1)×100
Коэффициент прироста (Кпр )**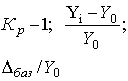
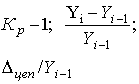
Темп прироста (Тпр)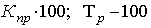
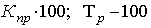
Абсолютное значение одного процента прироста (А)

^*
**

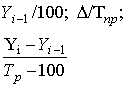
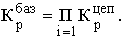
В случае, когда сравнение проводится с периодом (моментом) времени, начальным в ряду динамики, получают базисные показатели. Если же сравнение производится с предыдущим периодом или моментом времени, то говорят о цепных показателях.

Относительные показатели структуры характеризуют состав изучаемой совокупности, доли, удельные веса в общем итоге.

Удельный вес частей совокупности находится по формуле:

      Ci
     d = —– • 100%,

                 n

где:
              d – удельный вес;

    Ci – значение итого (от 1 до n) показателя;

    n – всего показателей совокупности.

Средние показатели. Средняя является обобщающей характеристикой совокупности единиц по качественно однородному признаку.

В статистике применяются различные виды средних: арифметическая, квадратичная, геометрическая и структурные средние: мода, медиана. Кроме моды и медианы, средние исчисляются в двух формах: простой и взвешенной. Выбор формы средней зависит от исходных данных и содержания определяемого показателя.

В данной работе будут рассчитаны: средняя арифметическая простая и средняя геометрическая.

Средняя арифметическая простая равна сумме значений признака деленной на их число:
             Уx    Ci + Ci + …      
     X = –— = –—–—–—–—.

    n           n

Где X – значение показателя (признака);
            n – число единиц показателя (признака).

Средняя арифметическая простая применяется в случаях, когда варианты представлены индивидуально в виде их перечня в любом порядке или ранжированного ряда.

Средний абсолютный прирост (средняя скорость роста) определяется как средняя арифметическая из показателей скорости роста за отдельные периоды времени:

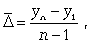
где y_n - конечный уровень ряда; y₁ - начальный уровень ряда.

Средний коэффициент роста ( 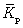) рассчитывается по формуле средней геометрической из показателей коэффициентов роста за отдельные периоды:

где К_р1 , К_р2 , ..., К_{р n-1} - коэффициенты роста по сравнению с предыдущим периодом; n - число уровней ряда.

Средний коэффициент роста можно определить иначе:

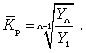
Средний темп роста , %. Это средний коэффициент роста, который выражается в процентах:

Средний темп прироста 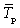, %. Для расчета данного показателя первоначально определяется средний темп роста, который затем уменьшается на 100%. Его также можно определить, если уменьшить средний коэффициент роста на единицу:

 = 95,4 – 100 = - 4,6%

Среднее абсолютное значение 1% прироста можно рассчитать по формуле

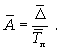
Показатели вариации

Показатели вариации — числовые характеристики статистического распределения, демонстрирующие степень рассеяния наблюдаемых значений измеряемого показателя относительно их среднего значения.

Чем выше показатели вариации, тем больший наблюдается разброс в значениях измеряемого показателя, и тем менее надежны результаты измерений. И наоборот: чем ниже показатели вариации, тем плотнее группируются наблюдаемые значения вблизи среднего значения, и тем достовернее результаты эксперимента.

К показателям вариации в статистике относятся:

· Размах вариации;

· Среднее линейное отклонение;

· Дисперсия;

· Среднее квадратическое отклонение;

· Коэффициент вариации.

Размах вариации вычисляется по формуле:

Среднее линейное отклонение рассчитывается по формуле:

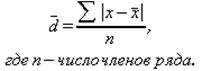
Дисперсия представляет собой средний квадрат отклонений вариантов от их средней величины, и вычисляется по формуле:

Среднее квадратическое отклонение равно квадратному корню из дисперсии, и рассчитывается как:

Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:

По величине коэффициента вариации можно судить о степени вариации признаков совокупностей. Чем больше его величина, тем больше разброс значений вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя. Совокупность считается количественно однородной, если коэффициент вариации не превышает 33%.