 |
Главная |
Нормализатор множества в группе. Центр группы
|
из
5.00
|
п.1 . В отличие от смежных классов. Классы сопряженных элементов не все равномощны. При вычисление их мощностей решающую роль играет понятие нормализатора.
Пусть M – подмножество, H –подгруппа группы G . Нормализатором множества M в подгруппе H называется множество:
NH(M)=  ,
, 
которое, как легко проверить, является подгруппой в H. Если не указано, в какой подгруппе H берется нормализатор, то это означает, что он берется во всей группе G. Очевидно, подгруппа тогда и только тогда нормальна в группе, когда её нормализатор совпадает со всей группой.
Теорема 1.4.1. Если M – подмножество, H – подгруппа группы G, то мощность класса подмножеств, сопряженных с M элементами из H, равна индексу  В частности,
В частности,
 .
.
Доказательство. Отобразим множества Mx, x Î H, на правые смежные классы группы H по подгруппе N = NH(M), полагая
(Mx)φ = Nx для xÎH .
Отображение φ однозначно, так как из Mx = My следует Nx = Ny . Отображение φ переводит разные элементы в разные , так как из Nx = Ny следует Mx = My. Наконец, φ – отображение на, так как каждое Nx имеет прообраз Mx. ■
Пусть M – подмножество, H – подгруппа группы G. Мы назвали нормализатором M в H совокупность тех элементов из H, которые перестановочны с множеством M в целом. Можно рассмотреть также множество тех элементов из H, которые перестановочны с M поэлементно, то есть
CH(M)=  .
.
Это множество называется централизатором множества M в подгруппе H. Если M состоит из одного элемента, то, конечно, его нормализатор и централизатор в H совпадают. Если не указано, в какой подгруппе H берется централизатор, то это означает, что он берется во всей группе G.
Централизатор всей группы G называется её центром и обозначается Z(G),
Z(G)=  .
.
Очевидно, что группа тогда и только тогда абелева, если она совпадает со своим центром. Ясно, что единица е всегда лежит в центре. Если других центральных элементов группа не содержит, то она называется группа с тривиальным центром. Заметим ещё, что любая подгруппа центра нормальна в группе.
Теорема 1.4.2. Пусть  , где p – простое число. Тогда центр Z(G) группы G нетривиальный, то есть содержит неединичные элементы.
, где p – простое число. Тогда центр Z(G) группы G нетривиальный, то есть содержит неединичные элементы.
Доказательство. Ранее было показано (см. 3), что любая группа G разбивается на не пересекающие классы сопряженных элементов. Среди классов будут одноэлементные образованные элементами центра, причем их число неравно нулю, так как единица е группы G образуют одноэлементный класс.
Пусть число элементов центра равно t. Все элементы, не принадлежащие центру Z(G), порождают классы сопряженных элементов. Обозначим  , классы сопряженных элементов содержащие более одного элемента. Число элементов в каждом таком классе есть индекс централизатора любого элемента класса (по теореме 1.4.1. учитывая, что нормализатор и централизатора одного элемента совпадают):
, классы сопряженных элементов содержащие более одного элемента. Число элементов в каждом таком классе есть индекс централизатора любого элемента класса (по теореме 1.4.1. учитывая, что нормализатор и централизатора одного элемента совпадают):

 .
.
Следовательно, по теореме Лагранжа  , где
, где  .
.
Тогда  , из этого равенства следует, что t делиться на p и так как
, из этого равенства следует, что t делиться на p и так как  , то
, то 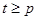 таким образом централизатор Z(G) группы G нетривиален. ■
таким образом централизатор Z(G) группы G нетривиален. ■
Далее докажем одно несложное утверждение которое понадобиться в дальнейшем.
Предложение 1.4.3. Фактор группа некоммутативной группы G по её центру Z(G) не может быть циклической.
Доказательство (от противного). Действительно, если G / Z(G) циклическая, то в смежном классе по Z являющимися образующим элементом этой циклической группы. Выберем некоторый элемент а. Подгруппа, порождающая этим элементом вместе с элементами из Z(G) совпадает со всей группой G. Из перестановочности между собой названных элементов следует коммутативность самой группы G –противоречие с условием. ■
Из доказанной выше теоремы 1.4.2 и предложения 1.4.3 вытекает следующее утверждение.
Теорема 1.4.4. Любая группа G порядка p2, где p – простое число, коммутативна.
Доказательство(от противного). Пусть G – не коммутативная группа, так как G является p -группой (конечная группа P является p -группой, если 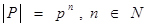 ), то её центр не единичен, то есть
), то её центр не единичен, то есть  . Рассмотрим G / Z(G). Порядок G / Z(G) равен p по теореме Лагранжа, следовательно, G / Z ( G ) – циклическая (см. следствие 2 теоремы Лагранжа) – противоречие с предложением 1.4.3. Таким образом G – коммутативна. ■
. Рассмотрим G / Z(G). Порядок G / Z(G) равен p по теореме Лагранжа, следовательно, G / Z ( G ) – циклическая (см. следствие 2 теоремы Лагранжа) – противоречие с предложением 1.4.3. Таким образом G – коммутативна. ■
п.2. Рассмотрим конструкцию, позволяющую по заданным группам строить новые группы. Одна из самых простых, но важных конструкций состоит в следующем.
Пусть A , B – группы, легко проверить, что множество 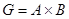 всех упорядоченных пар (a , b)где
всех упорядоченных пар (a , b)где  ,
, 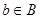 с бинарной операцией
с бинарной операцией  является группой. Она называется прямым произведением (внешним) групп A и B . При аддитивной записи групп, естественно говорить о прямой сумме
является группой. Она называется прямым произведением (внешним) групп A и B . При аддитивной записи групп, естественно говорить о прямой сумме  .
.
Теорема 1.4.5. Пусть G – группа с нормальными подгруппами A и B. Если 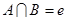 и AB = G, то
и AB = G, то  .
.
Доказательство .Из равенства AB = G следует, что любой элемент  записывается в виде g = ab, где
записывается в виде g = ab, где 
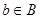 . Пусть ещё G = a1b1,
. Пусть ещё G = a1b1, 
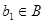 . Тогда
. Тогда  ,
, 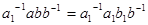 и
и  . Следовательно,
. Следовательно, 
 и мы пришли к выводу, что запись
и мы пришли к выводу, что запись  однозначна.
однозначна.
Далее, так как 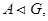 то коммутатор
то коммутатор  ; так как
; так как  , то
, то  , то есть, получаем
, то есть, получаем  и, стало быть
и, стало быть  .
.
Определим теперь отображение φ из  . Полагая
. Полагая  для любого
для любого 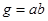 . Проверим закон сохранения операции. Согласно выше сказанному:
. Проверим закон сохранения операции. Согласно выше сказанному:


Это отображение является сюрьективным, ибо G = AB. Более того, отображение φ является взаимно однозначным так как если ab = a1b1 при  ,
, 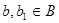 то, как это мы показали, выше a1= a , b1= b и, следовательно,
то, как это мы показали, выше a1= a , b1= b и, следовательно,  таким образом φ – удовлетворяет всем свойствам изоморфного отображения групп. ■
таким образом φ – удовлетворяет всем свойствам изоморфного отображения групп. ■
Группу G, удовлетворяющую условиям теоремы 1.4.5 принято называть (внутренним) прямым произведением своих подгрупп A , B. Отличие от внешнего прямого произведения состоит в том, что G содержит в качестве прямых множителей сами группы A , B, а не просто их изоморфные копии 
 ,
, 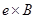 .
.
Последние определение прямого произведения (внутреннего). Можно заменить следующим ему эквивалентным. Группа G есть прямое произведение своих подгрупп  , если
, если
1) Элементы из любых двух подгрупп Hi и Hj,  , перестановочны между собой.
, перестановочны между собой.
2) Всякий элемент g и G однозначно записываются в виде произведения
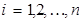
 где
где 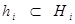 ,
,
|
из
5.00
|
Обсуждение в статье: Нормализатор множества в группе. Центр группы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

