Теоремы о гомоморфизмах

Пусть G – группа и P – другая группа. Пусть каждому элементу a Î G сопоставлен некоторый элемент из S, то есть, дано отображение G и S. Отображение φ называется гомоморфным или гомоморфизмом G в S, если произведение элементов из G соответствует произведение их образов, то есть

φ( a₁a₂)= φ(a₁)φ(a₂), где φ(a) – образ a Î G при отображение φ.

Предложение 1.5.1.Гомоморфным образом φ(G) группы G является группой. Образом единицы группы G является единица образа, и взаимно обратным элементом G соответствуют взаимно обратные образы.

Доказательство. φ(ab)= φ(a)φ(b) означает, что произведение двух элементов из φ(G)Î φ(G). Ассоциативность следует из ассоциативности в G и S. Равенство φ(a)=φ(1a)=φ(1)φ(a) показывает, что φ(1) есть левая единица для φ(G). А φ(а^–1)φ(а)=φ(а^–1а)=φ(1) показывает, что φ(а^–1) есть левый обратный элемент для φ(а) в φ(G). Это достаточно для заключения, что φ(G) есть группа (так как φ(а)=φ(а 1)=φ(а)φ(1) и φ(а)φ(а^–1)=φ(аа^–1)=φ(1)). ■

Гомоморфизм G в S, при котором различным элементам из G сопоставляется различные элементы в S.

Всякое изоморфное отображение группы G на себя называется автоморфизмом. Если в группе G выбран некоторый элемент а, то отображение, переводящее всякий элемент х этой группы в элемент

а^–1ха, то есть трансформирование всей группы элементов а, будет автоморфизмом группы G. Действительно, из а^–1ха=а^–1ya следует x = y, то есть отображение взаимно однозначно. Равенство х=а^–1(аха^–1)а

показывает, что при этом отображении всякий элемент группы будет образом некоторого элемента. Из соотношения a^–1xa· a^–1ya = a^–1(xy)a

следует изоморфизм рассматриваемого отображения. Такой автоморфизм группы G называется её внутренним автоморфизмом.

Пусть φ – гомоморфное отображение группы G на группу S. Множество всех элементов из G, имеющих один и тот же образ х Î S, называется полным прообразом элемента х и обозначается φ^–1(х). Полный прообраз единицы группы S называется ядром гомоморфизма.

Предложение 1.5.2. Ядро гомоморфизма φ группы G на группу S является нормальной подгруппой группы G.

Доказательство. Введем обозначение H для ядра. Если a Î H, то

a^–1Î H, ибо

φ(a^–1)=(φ(a))^–1=1. Если a Î H и b Î H, то ab Î H, ибо φ(ab)= φ(a)φ(b)=1·1=1. Наконец, если a Î H и c Î G, то c^–1ac Î H, ибо

φ(c^–1ac)= φ(c)^–1φ(a)φ (c)= φ(c)^–11φ(c)=1. ■

Предложение 1.5.3.В условиях предложения 1.5.2. полные прообразы элементов из S является классами смежности по ядру гомоморфизма.

Доказательство. Если a и b принадлежат одному классу смежности по H, то b = za при z Î H, тогда φ(b)=φ( z)·φ(a)=1·φ(a)=φ(a). Обратно, если φ(a)= φ(b), то φ(ab^-1)=1, так что ab^-1Î H , a Î Hb и b Î Hb. ■

Теорема 1.5.4. (первая теорема о гомоморфизме) Гомоморфный образ группы изоморфен её факторгруппе по ядру гомоморфизма.

Доказательство. Между образами при гомоморфизме и элементами факторгруппы имеется взаимно однозначное соответствие, в силу предложения 1.5.3. Оно сохраняется при умножении, ибо

φ((Ha)·(Hb))= φ(Ha)·φ(Hb).

Остается доказать любая ли нормальная подгруппа может быть принята за ядро гомоморфизма. Ответ положительный, так как отображение группы G на факторгруппу G / H по нормальной подгруппе H, заключающиеся в том, что каждому элементу группы G сопоставляется содержащий его класс смежности, есть гомоморфизм, и его ядро совпадает с H (это следует из определения умножение классов смежности как элементов факторгруппы). ■

Предложение 1.5.5. H и K подгруппы группы G и , тогда 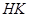 является подгруппой группы ,  и .

Доказательство. Пусть  причем  тогда рассмотрим (hk)^–1= k^-1h^-1 (по одному из основных свойств группы):

, причем , так как  поэтому,  таким образом, для каждого элемента 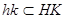 существует обратный .

Пусть , причем ,  тогда

 где  и поэтому , то есть условие замкнутости выполняется, таким образом, в силу предложения 1.1.1. можем считать, что HK является подгруппой группы G.

Кроме того, так как для любого , то Hk = kH , следовательно, HK = KH . Далее для любого элемента  имеем . Откуда . ■

Теорема 1.5.6 (об изоморфизме). Пусть G – группа и H и K две его подгруппы. Причём 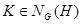 тогда  и .

Доказательство. Покажем что подгруппа  нормальна в K . Тогда для : 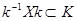, так как  и 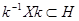,  и по условию , следовательно,  для любого k из K и значит 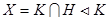. Кроме, того, по предыдущему предложению имеем HK = KH подгруппа группы G и .

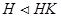Существует сюръективный гомоморфизм , сопоставленный каждому  смежный класс  группы 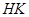 по подгруппе H. Несложно видеть  является ядром гомоморфизма, таким образом, по теореме 1.5.4. получаем:

. ■