 |
Главная |
Вторая и третья теорема Силова
|
из
5.00
|
Максимальная по вложению p-подгруппа конечной группы G называется силовской p -подгруппой группы G. Из доказанной теоремы вытекает в частности, что силовские p-подгруппы конечной группы, это в точности подгруппы порядка pt где pt – максимальная степень p делящий порядок группы.
Теорема 2.2.1. (вторая теорема Силова)
(Сопряженность) Все силовские p – подгруппы группы G сопряжены.
Доказательство.Пусть P – силовская подгруппа, если 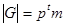 , где НОД( p , m )=1, то
, где НОД( p , m )=1, то 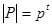 . Пусть, Δ как и раньше класс подгрупп, сопряженных с P элементами из G. Покажем, что если Q симметрическая p – подгруппа, то Q ÎΔ. Из теоремы 1.4.1. имеем
. Пусть, Δ как и раньше класс подгрупп, сопряженных с P элементами из G. Покажем, что если Q симметрическая p – подгруппа, то Q ÎΔ. Из теоремы 1.4.1. имеем
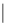 Δ
Δ 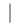 =
= 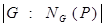 .
.
По теореме Лагранжа, получаем
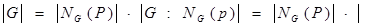 Δ
Δ 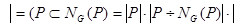 Δ
Δ 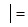
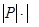 Δ
Δ 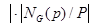 , НОД(
, НОД( 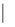 Δ
Δ 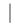 , p ), откуда
, p ), откуда 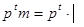 Δ
Δ 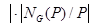 и, следовательно, разобьем Δ на подклассы подгрупп сопряженных между собой элементами из Q: Δ=Δ1È∆2… È∆k
и, следовательно, разобьем Δ на подклассы подгрупп сопряженных между собой элементами из Q: Δ=Δ1È∆2… È∆k
Если подгруппа S ÎΔi, то 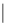 Δ
Δ 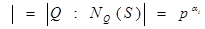 ,
, 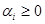 .
.
Следовательно, 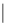 Δ
Δ 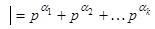 .
.
Отсюда так какНОД( 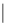 Δ
Δ 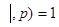 , то существует i такое что
, то существует i такое что 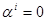 и Δi={S}. Таким образом, Sq = S и, значит,
и Δi={S}. Таким образом, Sq = S и, значит, 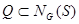 . Тогда по предложению 1.5.5.
. Тогда по предложению 1.5.5. 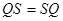 подгруппа группы G,
подгруппа группы G, 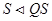 . Применяя теорему 1.5.6 (об изоморфизме) получаем:
. Применяя теорему 1.5.6 (об изоморфизме) получаем: 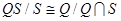 . Откуда получаем
. Откуда получаем 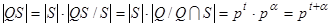 . Следовательно, по теореме Лагранжа порядок G делиться
. Следовательно, по теореме Лагранжа порядок G делиться 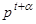 , но t – максимальная степень числа p, поэтому α=0 и
, но t – максимальная степень числа p, поэтому α=0 и 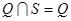 . Отсюда следует
. Отсюда следует 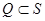 и значит Q = S (так как
и значит Q = S (так как 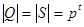 ). И так
). И так 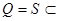 Δ, что и требовалось доказать.
Δ, что и требовалось доказать.
Теорема 2.2.2. (третья теорема Силова)
(Количество) Количество силовских p-подгрупп группы G сравнимо с 1 по модулю p и делит порядок G.
Доказательство.Пусть P – силовская p-подгруппа, Δ – класс всех подгрупп сопряженных с p элементами из G.
По теореме 2.2.1. (вторая теорема Силова) Δ совпадает с множеством всех силовских p-подгрупп так как
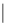 Δ
Δ 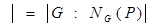 , по теореме Лагранжа
, по теореме Лагранжа
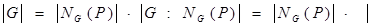 Δ
Δ 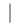 , то есть порядок G делиться на порядок Δ.
, то есть порядок G делиться на порядок Δ.
Разобьем Δ на подклассы подгрупп сопряженных между собой элементами из P:Δ={P}ÈΔ1È…ÈΔs, если подгруппа R ÎΔ, то |Δ|= 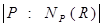 и, следовательно, |Δi|=
и, следовательно, |Δi|= 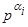 ,
, 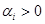 . Если
. Если 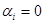 Δi={R} и
Δi={R} и 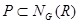 . В силу предложения 1.5.5. получаем что RP = PR подгруппы группы G и
. В силу предложения 1.5.5. получаем что RP = PR подгруппы группы G и 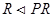 .
.
Далее по теореме 1.5.6. (об изоморфизме) получаем 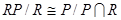 , следовательно,
, следовательно, 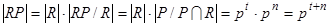 так как t – максимальная степень числа p, то n =0, отсюда следует
так как t – максимальная степень числа p, то n =0, отсюда следует 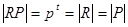 . Противоречие с тем что
. Противоречие с тем что 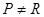 , поэтому
, поэтому 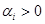 и, следовательно, имеем:
и, следовательно, имеем:
|Δ|= 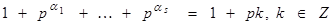 , таким образом, порядок |Δ |=1 (mod p). Теорема доказана. ■
, таким образом, порядок |Δ |=1 (mod p). Теорема доказана. ■
Теорема 2.2.3. Справедливо следующее утверждение:
i) Силовская р-подгруппа Р группы G нормальна в G тогда и только тогда, когда она единственна.
ii) Конечная группа G порядка 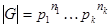 является прямым произведением своих силовских
является прямым произведением своих силовских 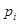 -подгрупп
-подгрупп 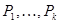 в точности тогда, когда все эти подгруппы нормальны в G.
в точности тогда, когда все эти подгруппы нормальны в G.
Доказательство:(i) Все силовские подгруппы, отвечающие данному простому делителю р порядка 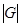 , по второй теореме Силова сопряжены. Условие единственности Р означает, что
, по второй теореме Силова сопряжены. Условие единственности Р означает, что 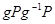 для любого элемента
для любого элемента 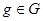 то есть
то есть 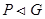 .
.
(ii) Докажем вначале
Необходимость. Пусть 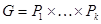 , где
, где 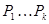 – силовские подгруппы группы G. Тогда в силу теоремы 1.4.5
– силовские подгруппы группы G. Тогда в силу теоремы 1.4.5 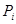 нормальна в G как любой прямой множитель.
нормальна в G как любой прямой множитель.
Достаточность. Пусть теперь 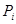 нормальна в G и
нормальна в G и 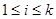 , то есть каждая силовская подгруппа
, то есть каждая силовская подгруппа 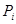 единственна в G. Заметим, во первых, что если
единственна в G. Заметим, во первых, что если 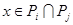 ,
, 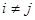
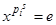 ,
, 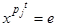 и, следовательно, x = e. Стало быть,
и, следовательно, x = e. Стало быть, 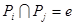 отсюда для любых
отсюда для любых 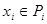 ,
, 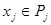 учитывая, что
учитывая, что 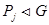 .
.
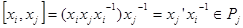 . С другой стороны, так как
. С другой стороны, так как 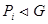 , то
, то
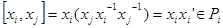 , отсюда следует,
, отсюда следует, 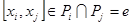 то есть элементы
то есть элементы 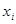 и
и 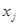 перестановочны.
перестановочны.
Пусть единичный элемент 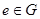 записан в виде
записан в виде 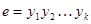 , где
, где 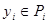 – элемент порядка
– элемент порядка 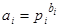 . Обозначив
. Обозначив 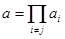 и воспользовавшись перестановочностью
и воспользовавшись перестановочностью 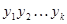 , получим
, получим
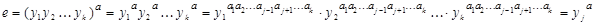 (1)
(1)
Учитывая, что 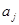 – это порядок элемента
– это порядок элемента 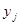 . Из последнего равенства (1) получаем
. Из последнего равенства (1) получаем 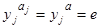 , так как
, так как 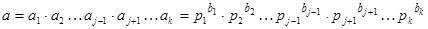 и
и 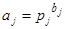 взаимно просто, то
взаимно просто, то 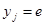 . Это верно при любом j, и, значит равенство
. Это верно при любом j, и, значит равенство 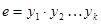 возможно лишь при
возможно лишь при 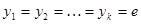 .
.
С другой стороны каждый элемент 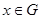 порядка
порядка 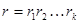 ,
, 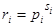 записывается в виде,
записывается в виде,
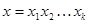 ,
, 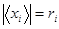 ,
, 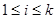 . (2)
. (2)
Достаточно положить 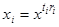 , где показатели определяются условиями
, где показатели определяются условиями
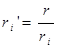 ,
, 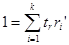 .
.
Предположим теперь, что х допускает другую запись в виде произведения 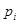 – элементов
– элементов 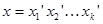 , то есть справедливо равенство
, то есть справедливо равенство 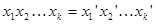 .
.
Домножим обе части равенства справа на 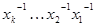 , получим
, получим
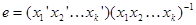
В силу перестановочности 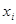 и
и 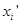 будем иметь
будем иметь
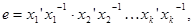
как было показано выше, влечет равенства 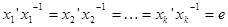 , то есть
, то есть 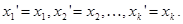
Таким образом, каждый элемент группы G записывается и притом единственным образом в виде (2), то есть смотри 4 п. 2 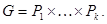 ■
■
2.3 Описание групп порядка pq
Теорема Силова часто дает весьма существенную информацию о данной конечной группе, а группы не очень большие позволяет описать полностью.
Пусть 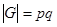 , p и q простые числа.
, p и q простые числа.
1. Рассмотрим первый случай, когда p = q, то есть порядок 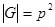 . Тогда по теореме 1.4.4. G – абелева.
. Тогда по теореме 1.4.4. G – абелева.
2. Пусть p и q по-прежнему простые числа, но 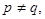 p < q.
p < q.
Тогда в группе G по первой теореме Силова существует силовские подгруппы порядка p и q, которые по следствию 2. теоремы Лагранжа будут являться циклическими.
Пусть 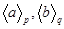 – силовские p- и q- подгруппы соответственно. По третьей теореме Силова число силовских q- подгрупп в G равно
– силовские p- и q- подгруппы соответственно. По третьей теореме Силова число силовских q- подгрупп в G равно
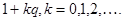 и делит pq. Откуда следует, что
и делит pq. Откуда следует, что 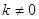 и подгруппа
и подгруппа 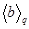 – единственна. В силу теоремы 2.2.3. (i):
– единственна. В силу теоремы 2.2.3. (i): 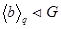 . Аналогично число силовских p-подгрупп равно
. Аналогично число силовских p-подгрупп равно 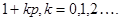 и делит pq. Здесь возможно два случая:
и делит pq. Здесь возможно два случая: 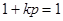 и
и 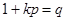 .
.
а) Силовская 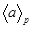 – единственна, тогда она нормальна в G. Применяя туже теорему 2.2.3., но уже пункт (ii), получаем, что
– единственна, тогда она нормальна в G. Применяя туже теорему 2.2.3., но уже пункт (ii), получаем, что 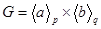 . По теореме 1.1.3.
. По теореме 1.1.3. 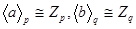 , следовательно,
, следовательно, 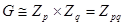 таким образом, в этом случае
таким образом, в этом случае 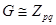 . ■
. ■
в) 1+ kp = q, то есть имеется q силовских p-подгрупп. Из условия 1+ kp = q следует 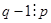 или
или 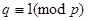 . В силу второй теоремы силова подгруппы
. В силу второй теоремы силова подгруппы 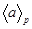 и
и 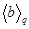 сопряжены. Пусть
сопряжены. Пусть
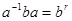 (1)
(1)
Если r =1, то 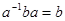 или ba = ab. Из последнего равенства следует, что
или ba = ab. Из последнего равенства следует, что 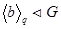 и значит, как и выше
и значит, как и выше 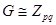 . Пусть
. Пусть 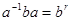 и r >1 тогда выясним, какое может быть r удовлетворяющее равенству (1). Из равенства (1) индукцией по x получаем
и r >1 тогда выясним, какое может быть r удовлетворяющее равенству (1). Из равенства (1) индукцией по x получаем 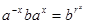 , откуда
, откуда
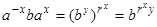 , (2)
, (2)
для всех целых x , y.
При x = p , y =1 из равенства (2) будем иметь вид 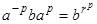 так как
так как 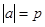 , то получаем
, то получаем 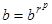 или
или 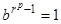 . Известно, что если элемент х группы G имеет порядок n, то
. Известно, что если элемент х группы G имеет порядок n, то 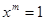 тогда и только тогда когда
тогда и только тогда когда 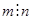 . Следовательно,
. Следовательно, 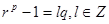 , то есть
, то есть 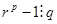 или
или 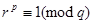 .
.
Кроме того, из равенства (2) можно получить более общую формулу умножения. Домножим равенство (2) слева на ах: 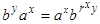 далее полученное равенство домножаем слева az:
далее полученное равенство домножаем слева az: 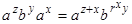 из полученного равенства умножаем, справа на элемент bt получаем
из полученного равенства умножаем, справа на элемент bt получаем
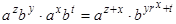 (3)
(3)
Обратно покажем, что если 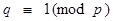 ,
, 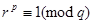 и r не сравнимо с 1 по (mod q) то формула (3) определяет неабелеву группу порядка pq.
и r не сравнимо с 1 по (mod q) то формула (3) определяет неабелеву группу порядка pq.
 Таким образом с помощью теоремы Силова мы описали все возможные типы групп порядка pq, при условии, что p < q их оказалось два – абелев и неабелев, причем второй существует только при условии
Таким образом с помощью теоремы Силова мы описали все возможные типы групп порядка pq, при условии, что p < q их оказалось два – абелев и неабелев, причем второй существует только при условии 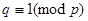 .
.
|
из
5.00
|
Обсуждение в статье: Вторая и третья теорема Силова |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

