Глава II . Теоремы Силова

Первая теорема Силова

Лемма 2.1.1. Пусть G конечная абелева группа порядка m и p –простое число, делящее m. Тогда G содержит подгруппу порядка p.

Для доказательства данного утверждения нам потребуется некоторые дополнительные понятия.

Пусть G – определена как и выше и a – некоторый элемент группы G натуральное число m такое, что a^m = e называется показателем элемента a . Среди показателей минимальным является порядок элемента a. ■

Лемма 2.1.2.Все показатели элемента делится на его порядок.

Доказательство.Пусть n – порядок элемента a, то есть aⁿ = e, m >0 другой показатель элемента. Тогда по теореме о деление с остатком получаем m = nq + r , 0≤ r ≤ n -1 и a^m = a^{nq + r} =( aⁿ ) ^q ∙ a^r = e ∙ a^r = a^r, так как 0≤ r ≤ n -1 то r может равняться только нулю и поэтому m = nq и, очевидно, m делится n. Лемма доказана. ■

Показатель группы G называется такое натуральное число m, что x^m = e для любого x Î G. Порядок группы принадлежит и числу его показателей.

Теперь возвратимся к доказательству Леммы 2.1.1. По условию леммы порядок группы G делиться на p. Если n делиться p, то в силу доказанного выше, в G существует элемент x такой что  делиться на p. Пусть , s Îℤ, тогда x^s≠ e x^ps =( x^s ) ^p = e, то есть элемент x^s имеет порядок p. И, следовательно, порожденная им циклическая подгруппа < x > тоже будет иметь порядок p. Лемма 2.1.1. доказана. ■

Теорема 2.1.3 ( первая теорема Силова). Пусть G – конечная группа порядка n , p – простое число. Тогда

a) (Существование) Для каждой степени p^α (α≥1) делящий n, в G существует подгруппа порядка p^α.

b) (Вложение) Если p^α делит порядок G, то каждая подгруппа порядка

p^α–1из G вложена в некоторую подгруппу порядка p^α из G.

Доказательство. а) Доказательство проведем индукцией по n.

1. При n =1 теорема очевидна (очевидна также теорема n =2, n =3).

2. Предположим, что теорема верна для всех групп порядков меньше n.

Далее рассмотрим два случая:

(i) Если Z центр группы G и порядок Z делиться на p. Тогда по лемме 2.1.1. так как Z – абелева группа и его порядок, делиться на p, то в Z существует подгруппа порядка p. То есть существует z Î Z такое, что , но любая подгруппа центра является нормальной подгруппой, следовательно 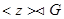. Рассмотрим фактор группу .

По теореме 1.2.1 (Лагранжа)  или

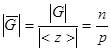 и, следовательно, порядок  делиться на  поэтому по индукционному предположению в  существует подгруппа  порядка , тогда полный прообраз подгруппы , подгруппа P в группе G, по теореме 1.2.1. (Лагранжа) будем иметь порядок :  следовательно, P – искомая подгруппа. (i) – доказано.

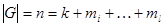(ii) Порядок k центра Z не делиться на p, то есть НОД( k , p )=1, тогда разобьем G на классы сопряженных элементов. Класс одноэлементен если состоит из элементов центра. Пусть , тогда , где  – не одноэлементные классы сопряженных элементов обозначим . Следовательно,  так как по условию  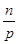и НОД( k , p )=1, то хотя бы одно из чисел  также должно быть взаимно просто с p.

По теореме 1.4.1. получаем, что если ,то мощность класса сопряженных с g элементов:

,

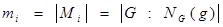учитывая что  – взаимно просто с p по теореме Лагранжа получаем, что  делиться на р^α по индукционному предложению так как порядок N_G ( g ) меньше порядка G, то в N_G ( g ) содержится подгруппа порядка p^α. Вместе с (ii) доказано и а).

b) Пусть  и порядок . Обозначим Δ– класс подгрупп сопряженных с P элементами из группы G. Рассмотрим два случая.

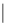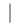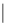(i) Порядок Δ и P взаимно просты, то есть НОД( Δ , P 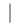)=1 по теореме 1.4.1. 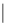Δ 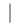= в силу теоремы Лагранжа, получаем:  и,  следовательно, Δ 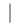отсюда следует, так как порядок G делится на 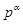,  и НОД( Δ , )=1, то  поэтому по пункту а): существует подгруппа  группы , . Откуда получаем, что полный прообраз подгруппы подгруппа H имеет

p^{α -1} ·p = p^α и .

(ii)

(iii) Порядок Δ делиться на p.

Пусть Δ={P}ÈΔ₁È…ÈΔ_m,Δ– это разбиение на подклассы подгрупп сопряженных с P . Если порядок Δ= m +1, то

Δ= ,

Δ=

(Обозначим Δ₁ – подклассы подгрупп сопряженных с P₁, Δ₂ – подклассы подгрупп сопряженных с P₂ и т. д.). Тогда если Q_iÎΔ_i, то

Δ 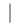= – по теореме 1.4.1. так как по теореме Лагранжа

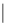, то Δ_i 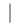= p^α, где 0≤α≤α-1.

Откуда 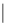Δ = и по условию порядок Δ делиться на p. Следовательно, должно существовать i – такое, что α _i =0 и Δ_i =1, значит, в подклассе Δ_i лежит только одна подгруппа. Пусть Δ_i={Q}, тогда для любого p Î P: p^–1Pp = Q то есть P нормализует Q и . Далее применяя предложение 1.5.5 получаем, что PQ подгруппа группы G, причем . Применяя теорему 1.5.6. (об изоморфизме) имеем . Отсюда по теореме Лагранжа следует . Учитывая, что Q сопряжено с P получаем: , где β >0 (так как если β=0, то  и, следовательно , что неверно).

Сейчас применим к подгруппе PQ внутренний, автоморфизм группы G, который пересекает подгруппу Q в Q^g = P. Получаем, что образ подгруппы PQ при этом автоморфизме будет являться подгруппа.

,

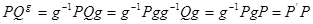причем P будет являться нормальной подгруппой группы P ^’ P. Рассмотрим фактор группу P ^' P / P, 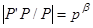, >0. Следовательно, P ^' P / P существует, по пункту а) подгруппа  порядка p. Тогда полный прообраз подгруппы  подгруппа H и будет являться искомой подгруппой порядка 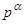. Пункт b) теоремы доказан полностью. ■