 |
Главная |
Теорема о разрешимости сравнения
|
из
5.00
|
Рассмотрим сравнение:

| (2.7) |
где  ,
, 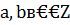 ,
, 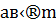 . Если
. Если 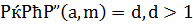 и
и 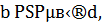 то сравнение не имеет решения.
то сравнение не имеет решения.
Пусть теперь  , тогда будем иметь:
, тогда будем иметь: 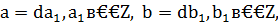
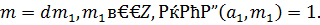
Поэтому получим: 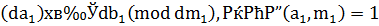 . Так как по определению НОД число
. Так как по определению НОД число 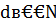 , то из последнего сравнения получим:
, то из последнего сравнения получим:
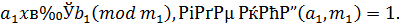
Таким образом, полагая в (1), что НОД 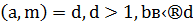 , мы пришли к сравнению такого же вида, но с условием:
, мы пришли к сравнению такого же вида, но с условием: 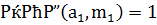 . Исследуем этот случай.
. Исследуем этот случай.
Теорема 1. Пусть дано сравнение (2.7) и НОД  . Тогда сравнение (2.7) имеет единственное решение.
. Тогда сравнение (2.7) имеет единственное решение.
Доказательство. Так как НОД  , то класс вычетов
, то класс вычетов  по mod m принадлежит мультипликативной группе классов вычетов, взаимно простых с mod m. Поэтому (по свойству группы) уравнение
по mod m принадлежит мультипликативной группе классов вычетов, взаимно простых с mod m. Поэтому (по свойству группы) уравнение 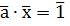 имеет единственное решение
имеет единственное решение  , где
, где 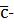 класс вычетов по mod m, взаимно простых с m. Значит, для
класс вычетов по mod m, взаимно простых с m. Значит, для 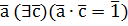 , но тогда
, но тогда 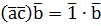 , отсюда
, отсюда 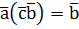 . Обозначим через
. Обозначим через  класс вычетов
класс вычетов 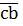 no mod m, тогда получим, что для
no mod m, тогда получим, что для 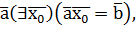 следовательно,
следовательно, 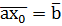 , a
, a  верное сравнение, то есть класс
верное сравнение, то есть класс  является решением сравнения (2.7). Это решение единственно, так как существует единственный класс
является решением сравнения (2.7). Это решение единственно, так как существует единственный класс 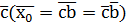 . Теорема 1 доказана.
. Теорема 1 доказана.
Пример 1. 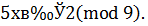 НОД (5,9) = 1, следовательно, сравнение имеет одно решение. Найдем его способом «подбора», то есть перебирая все числа из полной системы вычетов по mod m: {0, 1, 2, 3, 4, 5, б, 7, 8} (m = 9).
НОД (5,9) = 1, следовательно, сравнение имеет одно решение. Найдем его способом «подбора», то есть перебирая все числа из полной системы вычетов по mod m: {0, 1, 2, 3, 4, 5, б, 7, 8} (m = 9).
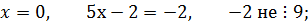
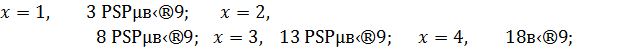
следовательно,  удовлетворяет сравнению, поэтому решением будет класс вычетов
удовлетворяет сравнению, поэтому решением будет класс вычетов 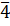 по mod m или, по-другому,
по mod m или, по-другому, 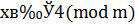 .
.
А так как данное сравнение имеет 1 решение, то остальные числа 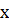 : 5, 6, 7, 8 проверять уже не надо.
: 5, 6, 7, 8 проверять уже не надо.
Ответ: 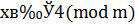 .
.
Заметим, что для нахождения решения сравнения первой степени с одной переменной (если оно есть) существует несколько способов:
1) подбора;
2) преобразования коэффициентов;
3) Эйлера (с помощью функции Эйлера);
4) цепных дробей.
Если модуль m является простым числом, то есть 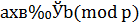 , число
, число 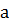 не делится на
не делится на  , то сравнение имеет единственное решение. Следовательно, множество классов вычетов
, то сравнение имеет единственное решение. Следовательно, множество классов вычетов 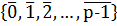 образует поле по отношению сложения и умножения классов вычетов. Его обозначают через
образует поле по отношению сложения и умножения классов вычетов. Его обозначают через 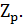
Пример 2. Вычислить остаток при делении 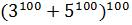 на 15.
на 15.
Решение. 1 способ. Сравнение 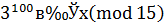 для применения теоремы Эйлера сократим на 3 (очевидно,
для применения теоремы Эйлера сократим на 3 (очевидно, 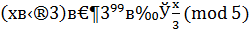 .
.
Так как 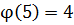 , то по теореме Ферма показатель 99 можно уменьшить по модулю 4. Получаем, что из
, то по теореме Ферма показатель 99 можно уменьшить по модулю 4. Получаем, что из 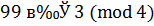 следует:
следует:
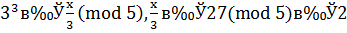 .
.
Умножаем на 3 обе части сравнения и модуль: 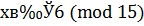 , т.е.
, т.е.
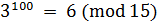 .
.
Аналогично вычисляем 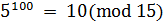 . Отсюда почленным сложением сравнений найдем:
. Отсюда почленным сложением сравнений найдем: 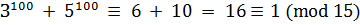 . Затем, возводя в 100-ю степень обе части сравнения, получаем
. Затем, возводя в 100-ю степень обе части сравнения, получаем 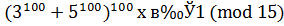 .
.
Ответ: 1.
2 способ. Сравнение 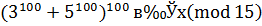 рассмотрим отдельно по модулям 3 и 5 (делители 15). Так как
рассмотрим отдельно по модулям 3 и 5 (делители 15). Так как 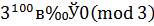 и
и 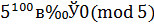 , то
, то
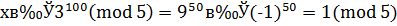 ,
,
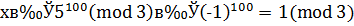 .
.
Среди целых чисел от 0 до 14 (возможные остатки при делении на 15) только 1, 6, 11 сравнимы с 1 по модулю 5. А среди этих трех только 1 сравнима с 1 по модулю 3, т.е.  . Тогда
. Тогда 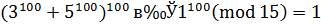 .
.
3 способ. Число 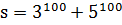 не делится на 3 (первое слагаемое делится, а второе не делится) и не делится на 5. Так как 3 и 5 есть простые числа, то
не делится на 3 (первое слагаемое делится, а второе не делится) и не делится на 5. Так как 3 и 5 есть простые числа, то  с ними взаимно просто и взаимно просто с 15. По теореме Эйлера
с ними взаимно просто и взаимно просто с 15. По теореме Эйлера
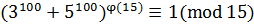 ,
, 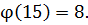
Ответ: 1.
Пример 3. Разложить 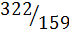 в цепную дробь. Проверить разложение, свернув цепную дробь последовательным вычислением подходящих дробей.
в цепную дробь. Проверить разложение, свернув цепную дробь последовательным вычислением подходящих дробей.
Решение. Найдём элементы цепной дроби как частные в алгоритме Евклида:
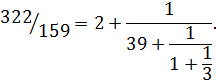
Сделаем сокращённую запись: 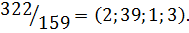
Пусть  обозначает
обозначает  элемент цепной дроби,
элемент цепной дроби, 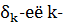 ю подходящую дробь,
ю подходящую дробь, 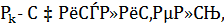
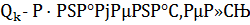
 подходящей дроби. Будем вычислять подходящие дроби по рекуррентной формуле
подходящей дроби. Будем вычислять подходящие дроби по рекуррентной формуле
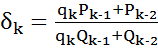 ,
,
используя схему:
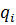
| 2 | 39 | 1 | 3 | |
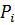
| 1 | 2 | 79 | 81 | 322 |
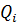
| 0 | 1 | 39 | 40 | 159 |
Как видно, последняя подходящая дробь совпадает с исходным числом.
Замечание. Непосредственное сворачивание конечной цепной дроби «снизу вверх» обычно громоздко:
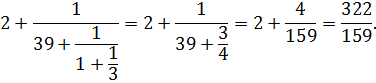
Задачи для самостоятельного решения.
Задача 1. Сократите дробь 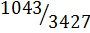 , применяя алгоритм Евклида.
, применяя алгоритм Евклида.
Задача 2. Сколько натуральных чисел взаимно просто с 520 и не превосходит это число? (решить с помощью функции Эйлера)
Задача 3. Решить сравнение 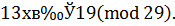
Задача 4. Найти все целочисленные решения уравнения 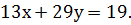
|
из
5.00
|
Обсуждение в статье: Теорема о разрешимости сравнения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

