Примеры использования закона распределения Pearson Type V

 

Варианты применения: Время выполнения какой-либо задачи (График функции плотности принимает форму, подобную форме графика плотности логнормального распределения, но может иметь большой острый “выступ” ближе к х=0)

Числовые характеристики закона распределения Pearson Type V

 

Параметр формы α > 0, масштабный параметр β > 0

Область[0,∞)

Среднее 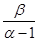для α > 1

 

Дисперсия 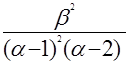для α > 2

 

Мода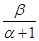

Оценка максимального правдоподобия

При наличии данных Х 1, Х 2, …, Х n подборка распределения gamma( 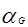, 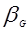) к 1/Х 1, 1/Х 2, …, 1/Х n , в результате дает оценки по методу максимального правдоподобия  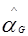и 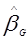. Оценки максимального правдоподобия для PT5(α,β) составляют 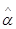=  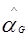и =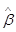

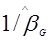
Примечания1. Тогда и только тогда X~ PT5(α,β), когда Y=1/X~gamma( 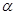,1/ 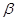). Поэтому распределение Пирсона типа V называют обращенным гамма - распределением.

2. Заметьте, среднее и дисперсия существуют только для определенных значений параметров формы.

Получение выборки с распределением Pearson Type V

Текст программы на C++

//kursml.cpp : main project file.

#include "stdafx.h"

#include "Pearson5.h"

using namespace System;

using namespace Variates;

using namespace System::IO;

int main(array<System::String ^> ^args)

{

TextWriter ^tr = File::CreateText(L"numbers.txt");

for(int i=0;i<100;i++)

{

tr->WriteLine((Pearson5::Sample(1,1).ToString());

}

tr->Close();

return 0;

}

Pearson5.h

#pragma once

#include "Rng.h"

#include "Gamma.h"

using namespace System;

namespace Variates

{

public ref class Pearson5 : public Rng

{

private:

double m_alpha;

double m_beta;

public:

Pearson5(double alpha, double beta) : m_alpha(alpha), m_beta(beta)

{}

virtual double Sample() override

{

return Sample(m_alpha, m_beta);

}

static double Sample(double alpha, double beta)

{

return 1 / Gamma::Sample(alpha, 1 / beta);

}

//FG(x) функция распределения случайной велечины с распределением GAMMA(gamma,1/beta)

virtual double DistributionFunction(double x) override

{return Pearson5::DistributionFunction(x, m_alpha, m_beta);}

//функция распределения F(x)

static double DistributionFunction(double x, double alpha, double beta)

{if (x > 0)

{return 1 - Gamma::DistributionFunction(1/x, alpha, 1/beta);//F(x)=1-FG(1/x)

}

else {return 0;}

}

virtual double DensityFunction(double x) override

{return Pearson5::DensityFunction(x, m_alpha, m_beta);}

//плотность f(x)

static double DensityFunction(double x, double alpha, double beta)

{if (x > 0)

{return Math::Pow(x, -(alpha + 1)) * Math::Exp(-beta / x) / Math::Pow(beta, -alpha) / Gamma::GammaFunction(alpha);}

else {return 0;}

}

};

}

Полученный по этой функции ряд представлен следующими значениями: (Объем выборки равен 43. Это ограничение обусловлено последующим использованием пакета Mathcad, в котором общее число элементов матрицы не должно превышать числа 600)

1,4898437906868

0,155118334154153

0,61232084606753

2,93030830346735

0,805146083946738

9,56457213164303

1,27783343504077

0,251137603293805

3,5276740403232

1,87120717537695

1,32530533009446

0,580380148657655

2,75653644757967

1,17443969975235

40,4251902165006

0,819370739897353

0,76435890601386

0,294787757136549

7,05592655012343

2,66917981096155

8,79281345418844

0,580093474185326

1,39633930229403

2,53700526140079

0,770494926092603

1,93265448451382

1,18590055703106

1,0792114387216

0,82818491346851

1,7150955462617

2,95934460597946

2,25523634892915

0,235192957404532

1,90816102397495

0,459223533552272

1,2301015212362

0,461599593338555

5,8725267553485

0,405012588940358

0,697295973424586

1,10547514222875

5,24774803293084

0,650277052201361