 |
Главная |
Постановка эксперимента
|
из
5.00
|
Для проведения исследований выбрана функция  +rnd, где
+rnd, где  – линейная функция, y1(x)=0.1+0.055x;
– линейная функция, y1(x)=0.1+0.055x; 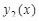 – гармоническая функция, y2(x)=2sin(x); rnd – шум. Переменная
– гармоническая функция, y2(x)=2sin(x); rnd – шум. Переменная  принимает значения от 0 до 42 с шагом, равным единице. Таким образом, длина N ряда
принимает значения от 0 до 42 с шагом, равным единице. Таким образом, длина N ряда  , равна 43. При этом длина окна
, равна 43. При этом длина окна  , число L-мерных векторов
, число L-мерных векторов  . Отдельно на рабочем листе MS Excel 2003 рассчитаны значения функций
. Отдельно на рабочем листе MS Excel 2003 рассчитаны значения функций  ,
, 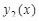 , rnd и
, rnd и  . При этом ряду
. При этом ряду  линейной функции, или тренда, соответствуют значения Gy1={gy10,gy11,…,gy142}={ 0.1, 0.155,..,2.41}. Ряд
линейной функции, или тренда, соответствуют значения Gy1={gy10,gy11,…,gy142}={ 0.1, 0.155,..,2.41}. Ряд  гармонической составляющей – Gy2={gy20,gy21,…,gy242}={ 0, 1.68,..,-1.83}, Rnd={1.84, 2.87,..,0.827} и G={1.94, 4.71,..,1.4}. Элементы ряда
гармонической составляющей – Gy2={gy20,gy21,…,gy242}={ 0, 1.68,..,-1.83}, Rnd={1.84, 2.87,..,0.827} и G={1.94, 4.71,..,1.4}. Элементы ряда  копируются в траекторную матрицу A на рабочем листе Mathcad 14.0. Сформированная матрица A является ганкелевой размером 22×22. Следует отметить, что размеры матрицы при ручном вводе ограничены возможностями Mathcad и не должны превышать 600 позиций. Сингулярные числа при сингулярном разложении траекторной матрицы A с применением функции svds() по формуле (4) принимают следующие значения: λ1=58.997; λ2=24.184; λ3=23.729. Остальные значения λ4,…,λ22 представляют убывающую последовательность: 5.404,…,0.228.
копируются в траекторную матрицу A на рабочем листе Mathcad 14.0. Сформированная матрица A является ганкелевой размером 22×22. Следует отметить, что размеры матрицы при ручном вводе ограничены возможностями Mathcad и не должны превышать 600 позиций. Сингулярные числа при сингулярном разложении траекторной матрицы A с применением функции svds() по формуле (4) принимают следующие значения: λ1=58.997; λ2=24.184; λ3=23.729. Остальные значения λ4,…,λ22 представляют убывающую последовательность: 5.404,…,0.228.
Сингулярное разложение в пакете Mathcad 14.0 реализуется с помощью функции svd() по формуле (6), формируется обобщенная матрица AS, включающая левые и правые сингулярные вектора. Левые и правые сингулярные вектора разделяются по формулам  и
и  соответственно.
соответственно.
Диагональная матрица ds сингулярных чисел определена по формуле (5). Для контроля правильности выполненных вычислений определяется равенство
 . (9)
. (9)
Для последующих расчетов определяются скалярные значения собственных чисел по формулам с использованием функции submatrix(). Например, для  (обозначение ds0 в пакете Mathcad)
(обозначение ds0 в пакете Mathcad)
 , (10)
, (10)
для  (обозначение ds1 в пакете Mathcad)
(обозначение ds1 в пакете Mathcad)
 и т. д. (11)
и т. д. (11)
Левые сингулярные вектора определяются из матрицы U аналогично с использованием функции submatrix():
 , (12)
, (12)
 и т. д. (13)
и т. д. (13)
Правые сингулярные вектора определяются в пакете Mathcad по формуле
 . (14)
. (14)
Элементарные матрицы Xi определены по формуле
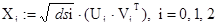 . (15)
. (15)
Таблица 5.1 – Исходные данные для исследования временного ряда
| Составляющие исходного ряда F(x)j | Потенциалы составляющих исходного ряда | |||||
| F(x)j | Тренд ax + b | Гармоника с·sinx | Шум rnd | φT | φS | φN |
| F(x)0 | 0.1+0.055x | 2sin(x) | rnd | 53.965 | 54.29958803 | 55.72192 |
| F(x)1 | 0.1+0.055x | 2sin(x) | 10rnd | 53.965 | 54.29958803 | 557.2192 |
| F(x)2 | 0.1+0.055x | 20sin(x) | rnd | 53.965 | 542.9958803 | 55.72192 |
| F(x)3 | 0.1+0.055x | 20sin(x) | 10rnd | 53.965 | 542.9958803 | 557.2192 |
| F(x)4 | 10(0.1+0.055x) | 2sin(x) | rnd | 539.65 | 54.29958803 | 55.72192 |
| F(x)5 | 10(0.1+0.055x) | 2sin(x) | 10rnd | 539.65 | 54.29958803 | 557.2192 |
| F(x)6 | 10(0.1+0.055x) | 20sin(x) | rnd | 539.65 | 542.9958803 | 55.72192 |
| F(x)7 | 10(0.1+0.055x) | 20sin(x) | 10rnd | 539.65 | 542.9958803 | 557.2192 |
Таблица 5.2 – Собственные числа при сингулярном спектральном анализе временных рядов F(x)j
| λi | F(x)0 | F(x)1 | F(x)2 | F(x)3 | F(x)4 | F(x)5 | F(x)6 | F(x)7 |
| λ1 λ2 λ3 λ4 λ5 λ6 λ7 λ8 λ9 λ10 λ11 λ12 λ13 λ14 λ15 λ16 λ17 λ18 λ19 λ20 λ21 λ22 | 58.997 24.184 23.729 5.404 5.331 4.454 4.112 4.01 3.807 3.768 3.482 3.422 3.086 2.903 2.373 2.24 1.895 1.859 1.566 1.499 1.361 0.228 | 330.15 54.463 53.732 46.596 46.365 43.26 40.101 38.279 37.603 35.482 34.728 34.278 29.542 28.412 23.721 22.454 18.883 18.838 15.537 15.097 13.484 2.384 | 223.425 222.2 57.172 5.416 5.35 4.443 4.102 4.01 3.798 3.757 3.488 3.426 3.089 2.909 2.382 2.24 1.877 1.858 1.56 1.494 1.357 0.25 | 341.176 241.956 231.45 54.212 53.4 44.113 40.123 38.356 37.702 35.491 34.692 34.329 30.376 29.281 23.91 22.49 18.965 18.889 15.569 15.08 13.554 2.392 | 324.008 24.177 23.928 20.601 5.364 5.315 4.408 4 3.821 3.721 3.501 3.415 3.116 2.83 2.395 2.245 1.922 1.891 1.553 1.508 1.358 0.226 | 584.944 54.45 53.799 46.612 46.361 43.463 41.141 40.081 37.987 37.556 34.953 34.267 29.906 28.273 23.596 22.454 18.847 18.601 15.643 15.088 13.586 2.354 | 333.228 222.05 212.455 20.592 5.378 5.335 4.408 4.009 3.819 3.707 3.498 3.408 3.118 2.839 2.407 2.253 1.93 1.896 1.563 1.504 1.361 0.244 | 590.12 241.876 237.353 54.179 53.45 44.394 41.084 40.101 37.999 37.62 34.924 34.289 30.824 29.121 23.802 22.481 18.879 18.641 15.694 15.082 13.672 2.364 |
|
из
5.00
|
Обсуждение в статье: Постановка эксперимента |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

