 |
Главная |
Пространства суммируемых функций.
|
из
5.00
|
Среди различных классов нормированных пространств, встречающихся в анализе, один из важнейших - это пространство суммируемых функций. Далее будем рассматривать именно эти нормированные пространства.
Определение. Пусть  – некоторое фиксированное измеримое множество из
– некоторое фиксированное измеримое множество из  . Пространством
. Пространством  , где
, где  ,называется нормированное пространство, элементами которого служат функции
,называется нормированное пространство, элементами которого служат функции  , измеримые и почти всюду конечные на
, измеримые и почти всюду конечные на  , для которых выполняется
, для которых выполняется 
Функции, эквивалентные друг другу на  , не различаются, а считаются за один и тот же элемент пространства
, не различаются, а считаются за один и тот же элемент пространства  . В частности, нулевой элемент в
. В частности, нулевой элемент в  – это совокупность всех функций, равных нулю почти всюду.
– это совокупность всех функций, равных нулю почти всюду.
Сложение элементов в  и умножение их на числа определяются как обычные сложение и умножение функций. Точнее, поскольку каждый элемент в
и умножение их на числа определяются как обычные сложение и умножение функций. Точнее, поскольку каждый элемент в  – это класс эквивалентных между собой функций, то для того, чтобы сложить два таких класса, нужно брать в них по представителю и потом суммой этих классов называют класс, содержащий сумму выбранных представителей. Результат не будет зависеть от выбора представителей в данных классах.
– это класс эквивалентных между собой функций, то для того, чтобы сложить два таких класса, нужно брать в них по представителю и потом суммой этих классов называют класс, содержащий сумму выбранных представителей. Результат не будет зависеть от выбора представителей в данных классах.
Определение. Число  называется нормой функции
называется нормой функции 
Будут выполняться все свойства нормы:
1.  и
и  почти всюду;
почти всюду;
2. 
3. 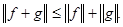
Первое свойство cледует из определения нормы и того, что 
Второе – из свойства интеграла: постоянный множитель можно выносить за знак интеграла. Третье свойство вытекает из неравенства Минковского: для любых функций 

Определение. Функция  называется ограниченной почти всюду, если существует неотрицательное число
называется ограниченной почти всюду, если существует неотрицательное число 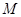 такое, что почти всюду выполняется неравенство
такое, что почти всюду выполняется неравенство  . (*)
. (*)
Определение. Пространством  называется нормированное пространство, элементами которого служат почти всюду ограниченные функции
называется нормированное пространство, элементами которого служат почти всюду ограниченные функции  . Нормой
. Нормой  называется наименьшая из констант, удовлетворяющих неравенству (*).
называется наименьшая из констант, удовлетворяющих неравенству (*).
Для  выполняется почти всюду неравенство
выполняется почти всюду неравенство  .
.
Через  будем обозначать линейное пространство измеримых функций, заданных на R.
будем обозначать линейное пространство измеримых функций, заданных на R.
Среди линейных операторов, действующих в пространстве 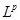 , рассмотрим следующие.
, рассмотрим следующие.
Определение. Оператор 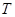 , действующий из пространства
, действующий из пространства 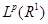 (
(  ) в
) в  , называется оператором слабого типа ( p , p ), если
, называется оператором слабого типа ( p , p ), если


 , где
, где 
 - мера множества, и оператором типа ( p , p ), если
- мера множества, и оператором типа ( p , p ), если 
 .
.
По определению оператор типа  является ограниченным, что равносильно его непрерывности.
является ограниченным, что равносильно его непрерывности.
Предложение 1. Любой оператор типа  есть оператор слабого типа
есть оператор слабого типа 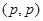 .
.
Доказательство.
Нужно доказать, что 
 .
.
Воспользуемся неравенством Чебышева:  .
.
Возьмем любое положительное число  . По неравенству Чебышева
. По неравенству Чебышева
 . Но по условию
. Но по условию  .
.
Учитывая последнее соотношение, имеем  , что и требовалось доказать.
, что и требовалось доказать.
|
из
5.00
|
Обсуждение в статье: Пространства суммируемых функций. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

