 |
Главная |
Интерполяционная теорема Рисса – Торина
|
из
5.00
|
И ее применение.
Прежде чем рассмотреть теорему Рисса – Торина и ее приложение, приведем определения и докажем факты, связанные с теорией банаховых пространств, которые понадобятся для этого.
Определение. Последовательность  метрического пространства Х называется фундаментальной, если
метрического пространства Х называется фундаментальной, если  .
.
Верно следующее утверждение.
Утверждение. Если последовательность  сходится, то она фундаментальная.
сходится, то она фундаментальная.
Обратно верно не всегда.
Определение. Метрическое пространство  называется полным, если в нем любая фундаментальная последовательность сходится.
называется полным, если в нем любая фундаментальная последовательность сходится.
Определение. Если пространство  , порожденное нормой, является полным, то линейное нормированное пространство называется банаховым.
, порожденное нормой, является полным, то линейное нормированное пространство называется банаховым.
Определение. Пусть  – банахово пространство,
– банахово пространство,  – подпространство в
– подпространство в 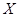 .
.  называется всюду плотным в Х, если
называется всюду плотным в Х, если  , т.е.
, т.е. 
 , такая, что
, такая, что  .
.
Утверждение 4 . Пусть оператор  , где
, где  плотно в
плотно в  – банахово пространство. Тогда оператор
– банахово пространство. Тогда оператор 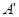 можно распространить на
можно распространить на  , т.е. существует оператор
, т.е. существует оператор 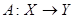 , такой, что
, такой, что  и
и  .
.
Доказательство.
Возьмем  из
из  . По определению существует последовательность
. По определению существует последовательность  из
из  такая, что
такая, что  стремится к
стремится к  , при
, при  стремящемся к
стремящемся к  .
.
Докажем, что  из
из  будет фундаментальной последовательностью. Тогда, т.к.
будет фундаментальной последовательностью. Тогда, т.к. 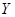 полное, последовательность
полное, последовательность  будет сходящейся.
будет сходящейся.
Возьмем произвольное положительное число  . Найдем номер
. Найдем номер  , для которого выполняется
, для которого выполняется  .Тогда
.Тогда

 . Следовательно, последовательность
. Следовательно, последовательность  фундаментальная.
фундаментальная.
Пусть  стремится к
стремится к  . Определим оператор
. Определим оператор  равенством
равенством  .
.
а) Проверим корректность определения оператора  .
.
Итак,  стремится к
стремится к  ,
,  стремится к
стремится к  . Возьмем другую последовательность
. Возьмем другую последовательность  , имеющую в пределе
, имеющую в пределе  . Тогда
. Тогда  будет стремится к некоторому элементу
будет стремится к некоторому элементу  .Составим новую последовательность
.Составим новую последовательность  Ее пределом будет
Ее пределом будет  . Пусть соответствующая последовательность
. Пусть соответствующая последовательность  стремится к
стремится к  . Из последней можно выбрать две подпоследовательности
. Из последней можно выбрать две подпоследовательности  и
и  , сходящиеся соответственно к
, сходящиеся соответственно к  и
и  .Следовательно,
.Следовательно,  и
и  , т.е.
, т.е.  и
и  совпадают.
совпадают.
б) Докажем линейность оператора А. Пусть 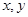
 Х;
Х;  - произвольные числа. Рассмотрим элемент
- произвольные числа. Рассмотрим элемент  . По определению существуют последовательности {xn},{yn}, такие, что
. По определению существуют последовательности {xn},{yn}, такие, что  . Тогда
. Тогда  .
.

 .
.
Получили 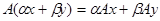 , что и означает по определению линейность оператора А. При этом, т.к. если
, что и означает по определению линейность оператора А. При этом, т.к. если  , то в качестве
, то в качестве  можно взять
можно взять  для всех n. Тогда
для всех n. Тогда  и
и  .
.
в) Докажем непрерывность оператора А.
Возьмем 
 .
. 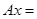
 ,
,  .
.

 . По теореме о предельном переходе в неравенстве будет выполняться неравенство
. По теореме о предельном переходе в неравенстве будет выполняться неравенство  . Т.к. по определению
. Т.к. по определению  - это наименьшая из констант, удовлетворяющих данному неравенству, то
- это наименьшая из констант, удовлетворяющих данному неравенству, то 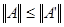 . (*)
. (*)
С другой стороны, по определению  ,
,  . Так как
. Так как  , то
, то  . (**)
. (**)
Учитывая неравенства (*) и (**) , установили равенство 
 . Таким образом, утверждение доказано.
. Таким образом, утверждение доказано.
Определение. Функция  называется простой, если она представляет собой конечную линейную комбинацию характеристических функций попарно непересекающихся измеримых множеств
называется простой, если она представляет собой конечную линейную комбинацию характеристических функций попарно непересекающихся измеримых множеств  , где
, где 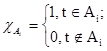 .
.
Теорема Лебега. Если последовательность  на
на  сходится к
сходится к  и при всех
и при всех 
 , где
, где  суммируема на
суммируема на  , то предельная функция
, то предельная функция  суммируема на
суммируема на  и
и  .
.
Предложение 4. Множество простых функций всюду плотно в  , т.е.
, т.е. 

 , такая, что
, такая, что  ,где
,где  – простая функция.
– простая функция.
Доказательство.
I.Обозначим  , где
, где  N.
N.
 |
Ясно, что для почти всех 
 . Тогда
. Тогда  для почти всех
для почти всех  . Следовательно,
. Следовательно,  .
.
С другой стороны,  (*)
(*)  ,т.е.
,т.е.  . Поэтому
. Поэтому  суммируема. Применим теорему Лебега к неравенству (*) :
суммируема. Применим теорему Лебега к неравенству (*) :  . Получим, что
. Получим, что  и, значит, приблизили
и, значит, приблизили  функциями
функциями  . Возьмем произвольное положительное число
. Возьмем произвольное положительное число  . Найдем функцию
. Найдем функцию  такую, что
такую, что  .
.
II. Приблизим  ступенчатой функцией.
ступенчатой функцией.
Обозначим  , где
, где  . Положим
. Положим  .
.
По свойству интеграла Лебега для любого положительного  найдется
найдется  , такое, что
, такое, что  . Это означает, что
. Это означает, что  .
.
Отрезок  разобьем на
разобьем на  равных частей точками
равных частей точками  так, чтобы
так, чтобы  .
.
Обозначим 

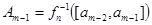 .
.
Рассмотрим функцию  . Тогда
. Тогда  . Следовательно,
. Следовательно,  , т.е.
, т.е.  .
.
В результате нашлась простая функция  такая, что
такая, что
 .
.
III. Таким образом, 
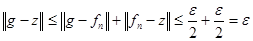 . Предложение доказано.
. Предложение доказано.
Первая интерполяционная теорема в теории операторов была получена М.Риссом в 1926 году в виде некоторого неравенства для билинейных форм. Ее уточнение и операторная формулировка были даны Г.О.Ториным. Вся теория интерполяции линейных операторов первоначально развивалась в направлении обобщения этой теоремы. Дадим ее формулировку.
Теорема. Пусть 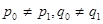 . Оператор Т действует из пространства
. Оператор Т действует из пространства  в
в  с нормой
с нормой  и одновременно из
и одновременно из  в
в  с нормой
с нормой  .Тогда Т будет непрерывным оператором из пространства
.Тогда Т будет непрерывным оператором из пространства  в
в  с нормой
с нормой  , удовлетворяющей неравенству
, удовлетворяющей неравенству  при условии, что 0<t<1 и
при условии, что 0<t<1 и  ;
;  .
.
Теперь рассмотрим приложение теоремы Рисса – Торина в доказательстве следующего факта.
Теорема. Пусть  и для чисел
и для чисел  выполняется равенство
выполняется равенство  .Тогда свертка
.Тогда свертка  .
.
Доказательство.
Нужно доказать, что 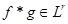 , т.е.
, т.е.  . Зафиксируем произвольную функцию
. Зафиксируем произвольную функцию  из
из  . Докажем сначала требуемый результат для частного случая, когда функция g простая, а затем распространим на произвольные функции g.
. Докажем сначала требуемый результат для частного случая, когда функция g простая, а затем распространим на произвольные функции g.
I. Пусть функция  простая.
простая.
1) Рассмотрим оператор свертки на множестве простых функций и проверим, что он типа 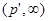 , где
, где  . В силу неравенства Гельдера
. В силу неравенства Гельдера  . Учитывая геометрический смысл
. Учитывая геометрический смысл  интеграла, получим
интеграла, получим 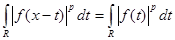 для любого действительного числа х. Тогда
для любого действительного числа х. Тогда  . Так как
. Так как  , то
, то  , т.е. равна некоторому числу
, т.е. равна некоторому числу 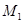 . Таким образом,
. Таким образом,  . Следовательно, нашлась константа
. Следовательно, нашлась константа 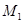 , такая, что
, такая, что  . Это и означает, что оператор свертки Т на множестве простых функций типа
. Это и означает, что оператор свертки Т на множестве простых функций типа  .
.
2) Проверим, что оператор Т типа  , т.е.
, т.е. 
 .
.
Рассмотрим случай, когда функция g имеет вид: 
 .
.

 .
.
Обозначим 
 .
.
Тогда правая часть равенства примет вид 

 по неравенству Минковского. (1)
по неравенству Минковского. (1)
Рассмотрим первое слагаемое 

 (2) Аналогично второе слагаемое
(2) Аналогично второе слагаемое


 . (3)
. (3)
Таким образом, учитывая (1),(2),(3), получим  . Найдем
. Найдем
 , т.к.
, т.к.  .
.
Далее имеем
 . В результате,
. В результате,  ,т.к.
,т.к. 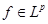 , то
, то  и равна некоторому числу
и равна некоторому числу  .
.
Совершенно аналогично доказывается  для случая, когда
для случая, когда  .
.
1) Таким образом, из пунктов I.1 и I.2 получим, что  типа
типа  и
и  , и,
, и,
следовательно,  будет типа
будет типа  при условии
при условии  , где
, где  .
.
 ;
;  , т.е.
, т.е.  , что и дано по условию.
, что и дано по условию.
Таким образом, применив теорему Рисса – Торина, установили истинность доказываемого утверждения для всех простых функций  .
.
II. Пусть  – произвольная функция из
– произвольная функция из  .
.
По предложению 4 множество простых функций всюду плотно в  .
.
По утверждению 4 оператор свертки  можно распространить на
можно распространить на  и тогда доказываемый факт верен для любой функции
и тогда доказываемый факт верен для любой функции  из
из  . Теорема доказана.
. Теорема доказана.
|
из
5.00
|
Обсуждение в статье: Интерполяционная теорема Рисса – Торина |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

