 |
Главная |
Интеграл Лебега – Стилтьеса.
|
из
5.00
|
Далее понадобится понятие интеграла Лебега – Стилтьеса. Введем это понятие.
Определение. Пусть на R задана монотонно неубывающая функция 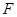 , которую для определенности будем считать непрерывной слева. Определим меры всех сегментов, интервалов и полусегментов равенствами
, которую для определенности будем считать непрерывной слева. Определим меры всех сегментов, интервалов и полусегментов равенствами
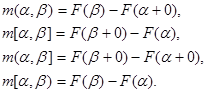
Таким образом, функция  , которая каждому сегменту ставит в соответствие меру этого сегмента, будет:
, которая каждому сегменту ставит в соответствие меру этого сегмента, будет:
1. принимать действительные неотрицательные значения;
2. аддитивной, т.е. мера объединения есть сумма мер этих сегментов.
Применив стандартное распространение меры, получим меру на некоторой  - алгебре.
- алгебре.
Определение. Меру  , получающуюся с помощью такого построения, называют мерой Лебега – Стилтьеса, отвечающей функции
, получающуюся с помощью такого построения, называют мерой Лебега – Стилтьеса, отвечающей функции  , а саму функцию
, а саму функцию  называют производящей функциейэтой меры.
называют производящей функциейэтой меры.
Определение. Пусть  - мера на R, порожденная монотонной функции
- мера на R, порожденная монотонной функции 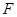 . Для этой меры обычным образом определяется класс суммируемых функций и вводится понятие интеграла Лебега
. Для этой меры обычным образом определяется класс суммируемых функций и вводится понятие интеграла Лебега  .
.
Такой интеграл, взятый по мере  , отвечающей производящей функции
, отвечающей производящей функции 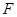 , называется интегралом Лебега – Стилтьесаи обозначается
, называется интегралом Лебега – Стилтьесаи обозначается  .
.
Теперь докажем факт, который используется при доказательстве интерполяционной теоремы.
Предложение 2. 


 и для
и для 
 и
и  , тогда
, тогда
(1)  , и если
, и если  , и
, и  , то
, то
 . (2)
. (2)
Доказательство.
Равенство (1) следует из определения интегралов Лебега и Лебега – Стилтьеса:
Если  - последовательность разбиений действительной оси:
- последовательность разбиений действительной оси:
 , и
, и  , то интегралы
, то интегралы  , где
, где 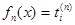 , если
, если  , стремятся при
, стремятся при  .
.
С другой стороны:
 при
при  .
.
Это и доказывает равенство (1).
Пусть теперь  . По (1), учитывая, что
. По (1), учитывая, что 
 , получаем
, получаем  (2’)
(2’)
При 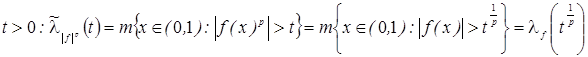
Следовательно, из соотношения (2’), делая замену переменных  , получим первое равенство (2).
, получим первое равенство (2).
Далее, для любого  выполняется
выполняется

(интегрирование по частям:  ).
).
Для доказательства второго равенства в (2) достаточно устремить в последнем соотношении число  к
к  и использовать оценку:
и использовать оценку:
 при
при 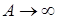 .
.
Предложение 2 доказано.
Замечание. Если функция  задана на
задана на  , то, применяя равенство (2) для функции
, то, применяя равенство (2) для функции 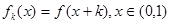 ,
,  , и учитывая, что
, и учитывая, что 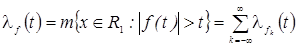 , получим
, получим
 (3)
(3)
Глава II . Интерполяция в пространствах суммируемых функций.
Теорема Марцинкевича и ее применение.
Одной из важнейших в теории интерполяции является теорема Ж.Марцинкевича, доказанная им в 1939 году. Прежде чем рассмотреть теорему, докажем предложение.
Пусть дана функция  . Положим для
. Положим для 
 ,
,  .
.
Предложение 3. Пусть  ,
,  , для любого положительного числа
, для любого положительного числа 
 и
и  – функции, описанные выше. Тогда
– функции, описанные выше. Тогда  .
.
Доказательство.

 |  |  |


 | ||||||||
| ||||||||
 |  | |||||||






Нужно показать, что  , т.е.
, т.е.  .
.
I. Для функции 
1) если 0<t 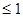 , то
, то  , т.к.
, т.к. 
2) Пусть t>1.
Обозначим  ,
,  .
.
 . Конечность
. Конечность  доказана в первом случае. Рассмотрим второй интеграл.
доказана в первом случае. Рассмотрим второй интеграл.
Покажем, что 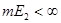 . Предположим противное, что
. Предположим противное, что  .
.
 , т.к.
, т.к.  . С другой стороны,
. С другой стороны,  . Но
. Но  на
на 
 , т.е.
, т.е.  , а это противоречие. Получили, что
, а это противоречие. Получили, что 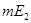 конечна и т.к. интеграл от ограниченной функции по конечной мере конечен, то
конечна и т.к. интеграл от ограниченной функции по конечной мере конечен, то  . Тогда
. Тогда  .
.
II.для функции  :
:
1) если  , то
, то  .
.
2) Пусть  .
.
Пусть 
 . Конечность
. Конечность  доказана в первом случае. Нужно показать, что
доказана в первом случае. Нужно показать, что  конечен.
конечен.
Докажем, что 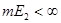 . Предположим противное, что
. Предположим противное, что  .
.
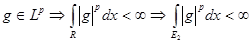 (
(  ).
).
С другой стороны  . Но
. Но  , т.е.
, т.е.
 . Пришли к противоречию.
. Пришли к противоречию.
Получили, что 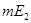 конечна и т.к. интеграл от ограниченной функции по конечной мере конечен, то
конечна и т.к. интеграл от ограниченной функции по конечной мере конечен, то  . Следовательно,
. Следовательно,  . Предложение доказано.
. Предложение доказано.
Следствие. Для всех  справедливо включение:
справедливо включение:  .
.
Замечание 2. Пусть оператор 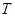 задан на пространстве
задан на пространстве  и на
и на  . Тогда оператор
. Тогда оператор  можно распространить с сохранением линейности до оператора, действующего из пространства
можно распространить с сохранением линейности до оператора, действующего из пространства
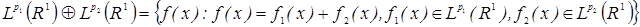 т.е.
т.е.  для любой функции
для любой функции 
Такое определение функции 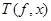 не зависит от выбора
не зависит от выбора  и
и 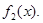 Действительно. Возьмем другое представление функции
Действительно. Возьмем другое представление функции  :
:
 , где
, где  т.е.
т.е.
 Нужно доказать, что
Нужно доказать, что 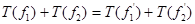 .
.
Из условия следует  . Левая часть равенства – это функция из
. Левая часть равенства – это функция из  правая часть - из
правая часть - из  Применим к равенству оператор T:
Применим к равенству оператор T:
 . Так как T линеен в пространствах
. Так как T линеен в пространствах  и
и  , то
, то  . Отсюда
. Отсюда  , что и требовалось доказать.
, что и требовалось доказать.
Теорема Марцинкевича. Если линейный оператор Т имеет слабый тип  и одновременно слабый тип
и одновременно слабый тип 
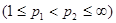 , то Т имеет тип
, то Т имеет тип  для любого
для любого  из интервала
из интервала 
Доказательство.
Считаем, что 
 . Фиксируем функцию
. Фиксируем функцию  и положительное число
и положительное число  . Оценим величину
. Оценим величину 
Пусть  и
и  функции, описанные выше.
функции, описанные выше.
Тогда  и
и  по замечанию 2.
по замечанию 2.
Следовательно, 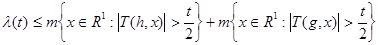 .
.
Используя оценки слабого типа 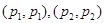 , находим, что при положительном
, находим, что при положительном 

 .
.
Из последнего неравенства и формулы (3) из замечания 1 получаем


 , т.е. оператор Т имеет тип
, т.е. оператор Т имеет тип  . Теорема доказана.
. Теорема доказана.
В качестве применения этой теоремы рассмотрим следующий пример.
Утверждение 2. Пусть  . Тогда оператор
. Тогда оператор  будет непрерывным оператором в пространстве
будет непрерывным оператором в пространстве  ,
,  .
.
Доказательство.
Рассмотрим два случая, когда  и
и  . Докажем, что оператор
. Докажем, что оператор  является оператором типа
является оператором типа  для этих случаев. Тогда по предложению 1
для этих случаев. Тогда по предложению 1  будет оператором слабого типа
будет оператором слабого типа  для
для  и
и  . Применив интерполяционную теорему Марцинкевича, получим, что
. Применив интерполяционную теорему Марцинкевича, получим, что  – оператор типа
– оператор типа  для любого
для любого  , а это равносильно его непрерывности.
, а это равносильно его непрерывности.
1)  и
и  . Докажем, что найдется число
. Докажем, что найдется число  , такое, что
, такое, что 



Учитывая последнее равенство и то, что для любого действительного числа  верно
верно  , получим
, получим
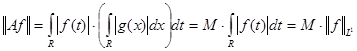 , где
, где  .
.
2) 
 .
.
Нужно доказать, что 
Для  почти всюду выполняется неравенство:
почти всюду выполняется неравенство:  . (*)
. (*)
Обозначим  ,
,  .
.
 . Так как
. Так как  , то
, то  .
.
Исходя из последнего соотношения и неравенства (*), получаем

 .
.
Таким образом, доказали, что оператор свертки  непрерывен в пространстве
непрерывен в пространстве  для любого р³1.
для любого р³1.
|
из
5.00
|
Обсуждение в статье: Интеграл Лебега – Стилтьеса. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

