Общие определения и обозначения

Бинарной алгебраической операцией на множестве 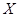 называют отображение декартова квадрата  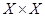во множество 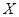. Если  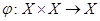- бинарная операция на 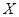, то каждой упорядоченной паре  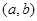элементов из  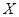соответствует однозначно определенный элемент 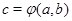. Бинарную операцию на  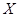обозначают одним из символов:  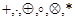и т.д. Если, например, вместо  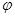условимся писать 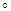, то вместо  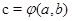пишем .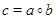

Говорят, что на множестве X определена бинарная операция (умножение), если 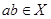 для всех .

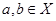Если 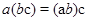 для всех 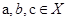, то операция называется ассоциативной.

Если 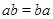 для всех 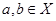, то операция называется коммутативной.

Элемент 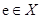 называется единичным, если  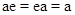для всех .

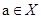Обратным к элементу 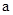 называется такой элемент 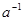, что .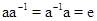

Полугруппой называется непустое множество 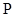 с бинарной алгебраической операцией (умножение), удовлетворяющей следующим требованиям:

(1) операция определена на 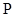, т.е.  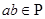для всех  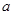и ;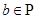

(2) операция ассоциативна, т.е. 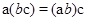 для любых .

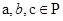Группой называется непустое множество 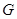 с бинарной алгебраической операцией (умножением), удовлетворяющей следующим требованиям:

(1) операция определена на 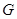, т.е.  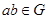для всех  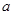и ;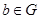

(2) операция ассоциативна, т.е. 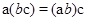 для любых ;

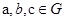(3) в 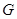 существует единичный элемент, т.е. такой элемент 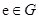, что 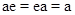 для всех ;

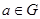(4) каждый элемент обладает обратным, т.е. для любого 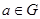 существует такой элемент 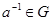, что .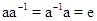

Группу с коммутативной операцией называют коммутативной или абелевой.

Если 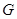 - конечное множество, являющееся группой, то G называют конечной группой, а число  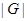элементов в  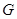- порядком группы .

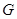Также группой называется непустое множество 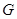 с бинарной алгебраической операцией (умножением), удовлетворяющей следующим требованиям:

(1) операция определена на ;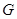

(2) операция ассоциативна;

(3) уравнения 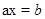,  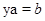имеют решения для любых элементов .

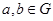Подмножество 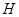 группы  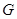называется подгруппой, если  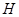- группа относительно той же операции, которая определена на группе 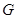. Для подгруппы используется следующее обозначение: 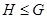. Запись  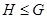читается так:  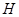- подгруппа группы .

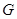Также можно дать следующее определение подгруппы конечной группы. Непустое подмножество 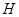 конечной группы  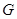называется подгруппой, если  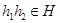для всех  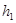и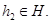

Собственной называется подгруппа, отличная от группы.

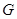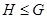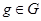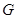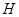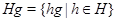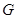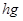Пусть  - группа,  и . Правым смежным классом группы  по подгруппе  называется множество всех элементов группы  вида , где 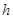 пробегает все элементы подгруппы .

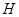Аналогично определяется левый смежный класс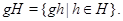

Если 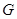 - конечная группа, то число различных правых смежных классов по подгруппе  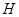также будет конечно, оно называется индексом подгруппы  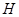в группе  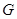и обозначается через .

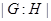Подгруппа 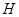 называется нормальной подгруппой группы 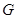, если  для всех 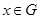. Запись  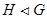читается так:  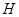- нормальная подгруппа группы  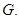Равенство  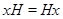означает, что для любого элемента  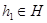существует элемент  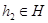такой, что .

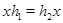Пусть 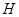 - нормальная подгруппа группы 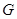. Обозначим через  совокупность всех левых смежных классов группы 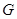 по подгруппе 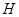, т.е. 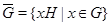. Группа  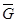называется факторгруппой группы  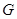по подгруппе  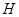и обозначается через .

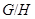Условимся через S 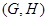 обозначать совокупность всех подгрупп группы 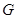, содержащих подгруппу 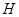. В частности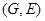, S = S 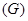 - совокупность всех подгрупп группы 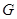, а S .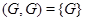

Каждая нормальная подгруппа 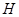 группы  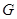определяет цепочку 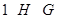. Обобщая эту ситуацию, цепочку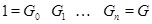

вложенных друг в друга нормальных подгрупп группы 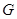 называют нормальным рядом в .

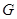Ряд называется субнормальным, если выполняется более слабое условие: каждый предыдущий его член есть нормальная подгруппа следующего члена, т.е. 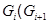 для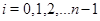

Члены субнормальных рядов называются субнормальными подгруппами (если подгруппа 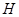 субнормальна в 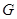, то пишут ( ).

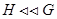Ясно, что каждый нормальный ряд является субнормальным.

Собственная подгруппа 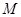 неединичной группы  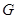называется максимальной подгруппой, если  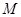не содержится ни в какой другой подгруппе, отличной от всей группы 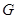, т.е. если из условия  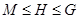следует, что  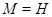или 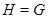. Для максимальной подгруппы  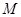неединичной группы  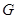используется запись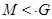

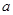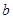В абелевой группе любые два элемента перестановочны. Если группа неабелева, то в ней существуют неперестановочные элементы, т.е. такие элементы  и , что 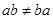. Поэтому естественно рассмотреть элемент 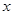, для которого 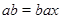. Отсюда .

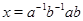Коммутатором элементов 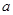 и 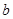 называют элемент 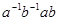, который обозначают через 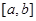. Ясно, что .

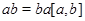Подгруппа, порождённая коммутаторами всех элементов группы 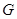, называется коммутантом группы  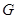и обозначается через 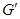. Таким образом, .

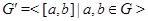Для любой неединичной подгруппы 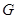 можно построить цепочку коммутантов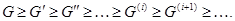

Если существует номер 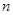 такой, что 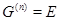, то группа  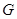называется разрешимой.

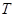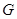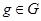Если  - непустое подмножество группы  и , то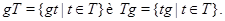

Элемент 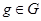 называется перестановочным с подмножеством 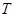, если 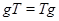. Равенство  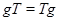означает, что для любого элемента  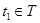существует такой элемент 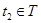, что 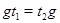. Если элемент  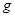перестановочен с подмножеством 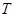, то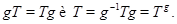

Совокупность всех элементов группы 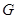, перестановочных с подмножеством  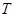называется нормализатором подмножества  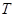в группе  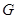и обозначается через 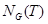. Итак,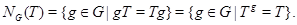

Пусть 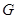 и 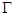 - мультипликативные группы. Отображение  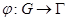называется гомоморфизмом группы  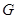в группу 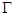, если  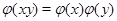для любых  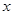и .

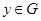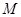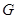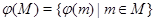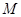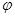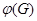Если  - подмножество группы , то  образ  при гомоморфизме , а  - образ гомоморфизма 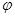. Образ гомоморфизма  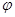также обозначают через .

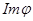Ядром гомоморфизма 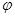 называется множество 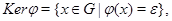где 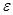 - единичный элемент группы 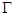. Другими словами, в ядре собраны все элементы группы 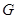, переходящие при отображении  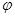в единичный элемент группы .

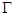Гомоморфизм 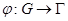 называется мономорфизмом, если 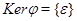. Из леммы 1 следует, что гомоморфизм  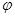является мономорфизмом тогда и только тогда, когда отображение  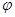- инъекция.

Если 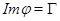, то гомоморфизм  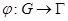называется эпиморфизмом. Ясно, что в этом случае  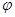- сюръекция.

Гомоморфизм, который одновременно является мономорфизмом и эпиморфизмом, будет изоморфизмом.