Определения и основные примеры подгрупповых функторов

Пусть  некоторый класс групп. Составим с каждой группой  некоторую систему ее подгрупп 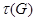. Будем говорить, что  - подгрупповой -функтор или подгрупповой функтор на , если выполняются следующие условия: 1)  для всех ;

2) для любого эпиморфизма , где А,  и для любых групп  и  имеет место  и

Подгрупповой -функтор  называется:

1) замкнутым, если для любых двух групп  и  имеет место ;

2) тривиальным, если для любой группы  имеет место

;

3) единичным, если для любой группы  система 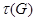 состоит из всех подгрупп группы G.

Тривиальный подгрупповой -функтор обозначается символом , а единичный - символом .

Если  и  - подгрупповой -функтор, то  - такой подгрупповой -функтор, что 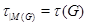 для всех . Такой функтор называется ограничением функтора  на классе .

Рассмотрим несколько примеров подгрупповых функторов. В случае, когда  - класс всех групп, подгрупповые -функторы мы будем называть просто подгрупповыми функторами.

Пример 1. Пусть для любой группы ,

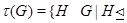
Понятно, что  - замкнутый подгрупповой функтор. Для обозначения такого подгруппового функтора мы применяем запись .

Пример 2. Пусть 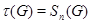 - совокупность всех нормальных подгрупп группы  для каждой группы . Такой функтор в общем случае замкнутым не является.

Пример 3. Пусть  - произвольное натуральное число. Для каждой группы  через  обозначим совокупность всех таких подгрупп , для которых . Понятно, что  - подгрупповой -функтор. Для обозначения такого функтора мы будем применять запись .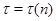

Пример 4. Пусть  - произвольное кардинальное число. И пусть для любой группы .

Понятно, что такой подгрупповой функтор в общем случае не является замкнутым. Для обозначения такого функтора мы применяем запись .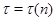

Если  - подгруппа группы , то символом  обозначается мощность множества .

Пример 5. Пусть  - простое число и пусть для любой группы 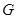 система  в  нет такой подгруппы , что ,  - натуральное число, взаимнопростое с .

Покажем, что  - подгрупповой функтор.

Действительно, пусть  и . Предположим, что

где  - натуральное число. Тогда  - натуральное число и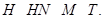

Следовательно, , и поэтому . Это означает, что . Аналогично, мы видим, что если

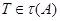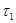то . Таким образом,  - подгрупповой функтор. Для обозначения такого подгруппового функтора мы используем запись . Заметим, что если  - некоторый класс конечных групп и , то  - замкнутый подгрупповой функтор.

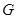Пример 6. Пусть . И пусть для каждой группы  множество  совпадает с совокупностью всех тех подгрупп из , индексы которых не делятся на числа из . Понятно, что  - замкнутый подгрупповой функтор. Для обозначения такого функтора мы будем применять запись .

Напомним, что подгруппа  группы  называется абнормальной в 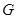, если всегда из  следует, что .

Пример 7. Пусть для любой группы  множество  совпадает с совокупностью всех абнормальных подгрупп группы . Легко видеть, что  - незамкнутый подгрупповой функтор. Для обозначения такого функтора мы будем применять запись .

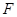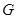Пример 8. Пусть  - произвольный класс групп. Подгруппа  группы  называется  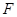- абнормальной в , если выполняется одно из следующих двух условий:

1) ;

2) 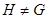 и для любых двух подгрупп  и  из , где  и  - максимальная подгруппа в  имеет место .

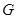Легко видеть, если группа  разрешима, то ее подгруппа  абнормальна в  тогда и только тогда, когда она -абнормальна в .

Сопоставляя каждой группе  множество всех ее 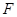-абнормальных подгрупп , получаем подгрупповой функтор, для которого мы будем применять запись .

Пример 9. Подгруппа  группы  называется 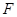-субнормальной в 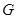, если выполняется одно из следующих двух условий:

1) ;

2) 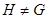 и в  имеется такая цепь подгрупп  где  - максимальная в  подгруппа, содержащая , .

Пусть 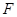 - некоторая непустая формация и для каждой группы  система  состоит из всех 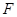-субнормальных в  подгрупп.

Покажем, что  - подгрупповой функтор. Пусть -субнормальна в . И пусть  и  - такие члены цепи (1), что , где  - нормальная в  подгруппа.

Покажем, что  - максимальная подгруппа в . Допустим, что  для некоторой подгруппы . Тогда поскольку  максимальна в , то либо , либо .

Пусть имеет место первое. Тогда поскольку , то . Противоречие. Значит, , т.е. 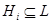. Поэтому . Противоречие. Итак, ряд  таков, что в нём для любого  имеет место одно из двух условий:

1) ;

2)  - максимальная подгруппа в . He теряя общности, мы можем считать, что все члены ряда (2) различны. Заметим, что поскольку  то

Итак,  - -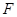субнормальная подгруппа в 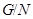. Понятно также, что если  - -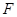субнормальная подгруппа в 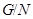, то  - -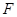субнормальная подгруппа в . Таким образом,  - подгрупповой функтор. Для обозначения такого функтора мы будем применять запись .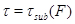

Класс групп называется гомоморфом, если он содержит все гомоморфные образы всех своих групп. Гомоморф конечных групп  называется формацией, если каждая конечная группа  обладает наименьшей по включению нормальной подгруппой (обозначаемой символом ) со свойством .

Лемма 3.1 Пусть 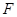 - формация, . Тогда

Доказательство. Пусть . Тогда

Отсюда следует, что . С другой стороны, поскольку  - гомоморф, то

Откуда получаем . Из  и  следует равенство .

Лемма доказана.

Пример 10. Пусть  - некоторый класс конечных групп и  - формация. Пусть для любой группы

Покажем, что  - подгрупповой  - функтор.

Действительно, пусть  и . Тогда , и поэтому, согласно лемме 3.1, мы имеем

Следовательно, . Аналогично, если , то . Следовательно,  - подгрупповой -функтор. Для обозначения такого функтора мы применяем запись .

Пример 11. Для каждой группы 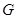 через  обозначим совокупность всех абнормальных максимальных подгрупп из 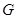. Понятно, что  - подгрупповой функтор. Для обозначения такого функтора мы будем применять запись .