Уравнения геодезических и эволюция функции распределения на римановом многообразии

Рассмотрим метрику gijdxidxj в пространстве Rn, x Rn, gij(x)-n2 функций. Это означает, что длина кривой определяется формулой:

                          (2.1)

а уравнение геодезических получается из принципа наименьшего действия (принципа наименьшей длины). Если, более обще, действие записывается в виде S = dt, где L—лагранжиан, то уравнения Эйлера-Лагранжа даются варьированием с фиксированными концами траекторий:

Получаем уравнения Эйлсра-Лагранжа:

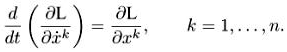
В случае геодезических L =  имеем

             (2.2)

Функционал длины инвариантен относительно замены t =  для любой гладкой функции , и то же свойство имеют уравнения (2.2).

Этим свойством иногда распоряжаются так, чтобы максимально упростить уравнения. Выберем[5] в качестве параметра длину линии (интервал, собственное время) s : ds = 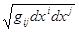, после деления на ds получим  = 1, и уравнения (2.2) превращаются в

                                 (2.3)

Последние совпадают с уравнениями Эйлера-Лагранжа для действия с лагранжианом

Преобразуем их к виду

       (2.4)

Здесь gki — матрица, обратная gij а  называются символами Кристоффеля.

Запишем уравнения (1.2) для функции распределения f(х, v, s) по пространству и скоростям (с длиной .s вместо времени) для уравнения (2.4), как это показано в предыдущем параграфе:

                   (2.5)

Последний член в левой части соответствует тому, что система (2.4) имеет дивергенцию, отличную от нуля. Переход к бездивергентному виду можно осуществить двумя способами.

Способ 1 . Переход к переменным координата-импульс и гамильтонов формализм.

Введем стандартным образом импульсы.[6] Если L = (gijxixj)/2 (этот лагранжиан дает те же уравнения движения, что и (2.1)), то импульсы pi = = dL/dxi= gijxj , а гамильтониан Н = pivi — L = (pipgij)/2. Тогда уравнения (2.3) приобретают гамильтонов вид

Упражнение

Показать, что для любой гамильтоновой системы дивергенция равна нулю.

Решение

Получаем уравнения для функции распределения f(s,х,р) по координатам и импульсам (1.2) в виде

                (2.6)

Эго уравнение имеет вид

df/ds + {Н, f} = 0, где {Н, f} — скобка Пуассона:

Способ 2. Переход к инвариантной мере в пространстве координаты-скорости.

Пусть g — определитель матрицы gij. Вместо f в (2.5) введем новую функцию распределения

F{x,v,s) = F(x,v,s)/g.

Упражнение

Показать, что для новой функции распределения уравнение эволюции бездивергентно и имеет вид

Решение

Воспользуемся операцией дифференцирования определителя. При этом второе слагаемое в (2.5) преобразуется следующим образом:

В (a) используется тождество

Для новой функции распределения число частиц записывается в виде

Поэтому g dxdv есть инвариантная мера: F не растет, т.е. полная производная от неё есть ноль, и поскольку число частиц сохраняется, то мера g dxdv сохраняется тоже.

Вывод. В качестве переменных в функции распределения можно брать импульсы или скорости, а в качестве времени — время или интервал s. Для простоты уравнений брали интервал, который в теории относительности называется собственным временем[7]. Возможность выбрать s в качестве параметра означает синхронизацию собственного времени различных частиц. С этим связан парадокс близнецов. Тот из них, чей интервал (собственное время) меньше, т.е. который «двигался больше», оказывается младше. Поэтому использование s хотя формально и возможно, но делает затруднительным интерпретацию результатов.